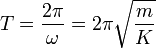Muelle vertical (GIA)
De Laplace
(Página creada con '== Enunciado == Se tiene un muelle vertical de constante <math>K</math> y longitud natural <math>l_0</math>. El sistema está sometido a la acción de la gravedad, <math>\vec{g}…') |
(→Movimiento de la masa) |
||
| (Una edición intermedia no se muestra.) | |||
| Línea 108: | Línea 108: | ||
T = \dfrac{2\pi}{\omega} = 2\pi\sqrt{\dfrac{m}{K}} | T = \dfrac{2\pi}{\omega} = 2\pi\sqrt{\dfrac{m}{K}} | ||
</math></center> | </math></center> | ||
| + | |||
| + | [[Categoría:Dinámica del punto material|1]] | ||
| + | [[Categoría:Física I (G.I.C.)]] | ||
| + | [[Categoría:Física I (G.I.A.)]] | ||
| + | [[Categoría:Física I (G.I.T.I.)]] | ||
última version al 09:15 2 oct 2014
Contenido |
1 Enunciado
Se tiene un muelle vertical de constante K y longitud natural l0. El sistema está sometido a la acción de la gravedad, 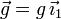 .
.
- Se cuelga una masa m del extremo del muelle. ¿Cuál es la nueva elongación del muelle cuando se alcanza el equilibrio?
- Partiendo de la situación del apartado anterior, estiramos la masa de modo que la elongación del muelle aumenta una distancia L, y lo soltamos. Describe las fuerzas actuando sobre la masa justo después de soltarla.
- Aplicando la Segunda Ley de Newton calcula la posición de la masa como función del tiempo. ¿Que movimiento describe?
Nota : Podemos suponer que todos los desplazamientos del muelle son verticales.
2 Solución
2.1 Elongación con masa m
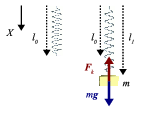
Si dejamos colgar el muelle verticalmente bajo la acción de la gravedad, su propio peso lo estira, oscila ligeramente y finalmente deja de moverse (alcanza el equilibrio) con una determinada longitud que llamaremos l0 . Cuando colgamos una masa m, el muelle se estira nuevamente. El equilibrio se restablece cuando el balance de fuerzas sobre la masa es cero, es decir, cuando se cumple la condición

Si escogemos el eje OX como se indica en la figura tenemos
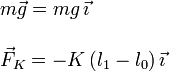
De este modo obtenemos la longitud de equilibrio del muelle con la masa m
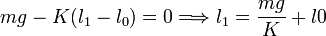
2.2 Aumento de la elongación una distancia L
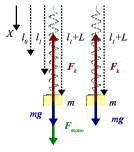
Si partiendo de la situación anterior estiramos con la mano, estamos añadiendo una fuerza que produce una nueva situación de equilibrio con una elongación
En ese momento las fuerza que actúan sobre la masa son el peso, la ejercida por la mano y la del resorte. Al soltar la masa, desparece la fuerza de la mano. En ese instante la suma total de fuerzas es distinta de cero, por lo que la masa adquiere una aceleración dada por la Segunda Ley de Newton
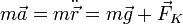
2.3 Movimiento de la masa
La Segunda ley de Newton nos proporciona la ecuación diferencial que determina el movimiento. En un instante dado la elongación del muelle es l(t). Como suponemos que todos los movimientos son verticales, la posición, velocidad y aceleración de la masa m son
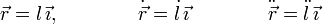
La fuerza ejercida por el muelle es

La ecuación de movimiento queda
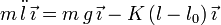
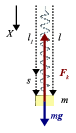
Vamos a describir el movimiento en función de la distancia s indicada en la figura adjunta. Tenemos
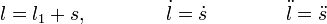
siendo l1 la posición de equilibrio alcanzada por el muelle cuando se le cuelga la masa m. Utilizando el resultado del apartado
anterior en la ecuación de l(t), y prescindiendo de los vectores  , pues el movimiento es unidimensional, la ecuación queda
, pues el movimiento es unidimensional, la ecuación queda

Las condiciones iniciales son velocidad inicial cero, pues parte del reposo, y elongación inicial l(t = 0) = l1 + L. Trasladadas a s(t) el problema queda

Las soluciones de esta ecuación son una combinación de exponenciales. En este caso, agrupamos las exponenciales en forma de senos y cosenos, de modo que buscamos una solución de la forma
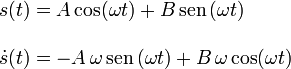
Imponiendo las condiciones iniciales obtenemos los valores de A y B
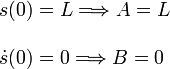
Por tanto la posición de la masa en función del tiempo viene descrita por la ecuación

La masa oscila con un período