2.2. Evolvente de una circunferencia
De Laplace
(→Vector de posición) |
m (3.2. Evolvente de una circunferencia trasladada a 2.2. Evolvente de una circunferencia) |
||
| (31 ediciones intermedias no se muestran.) | |||
| Línea 11: | Línea 11: | ||
==Vector de posición== | ==Vector de posición== | ||
| + | |||
| + | [[Archivo:evolvente.gif|right]] | ||
| + | |||
Por adición de vectores | Por adición de vectores | ||
| Línea 23: | Línea 26: | ||
<center><math>\frac{\overrightarrow{CP}}{|\overrightarrow{CP}|} = \,\mathrm{sen}(\omega t)\vec{\imath}-\cos(\omega t)\vec{\jmath}</math></center> | <center><math>\frac{\overrightarrow{CP}}{|\overrightarrow{CP}|} = \,\mathrm{sen}(\omega t)\vec{\imath}-\cos(\omega t)\vec{\jmath}</math></center> | ||
| - | El módulo de <math>\overrightarrow{CP}</math> lo da la cantidad de hilo desenrollado hasta ese momento, <math>L = A\omega t</math> | + | El módulo de <math>\overrightarrow{CP}</math> lo da la cantidad de hilo desenrollado hasta ese momento, igual al producto del radio por el ángulo, <math>L = A\omega t</math> |
| - | <center><math>\overrightarrow{CP}= | + | <center><math>\overrightarrow{CP}= A\omega t(\mathrm{sen}(\omega t)\vec{\imath}-\cos(\omega t)\vec{\jmath})</math></center> |
Sumando los dos vectores obtenemos el vector de posición | Sumando los dos vectores obtenemos el vector de posición | ||
| Línea 32: | Línea 35: | ||
==Velocidad y aceleración== | ==Velocidad y aceleración== | ||
| + | ===Velocidad=== | ||
| + | Derivando el vector de posición respecto al tiempo obtenemos | ||
| + | |||
| + | <center><math>\vec{v}(t)=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=A\omega^2 t\cos(\omega t)\vec{\imath}+A\omega^2t\,\mathrm{sen}(\omega t)\vec{\jmath}</math></center> | ||
| + | |||
| + | ===Aceleración=== | ||
| + | Derivando de nuevo | ||
| + | |||
| + | <center><math>\vec{a}(t) =\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=A\omega^2\left(\cos(\omega t)-\omega t\,\mathrm{sen}(\omega t)\right)\vec{\imath}+A\omega^2\left(\mathrm{sen}(\omega t)+\omega t\cos(\omega t)\right)\vec{\jmath}</math></center> | ||
| + | |||
| + | <center>[[Archivo:esquema-evolvente.png]]</center> | ||
| + | |||
==Ley horaria== | ==Ley horaria== | ||
| + | La rapidez con que se recorre la curva la da el módulo de la velocidad | ||
| + | |||
| + | <center><math>\dot{s}=|\vec{v}| = \sqrt{\vec{v}\cdot\vec{v}} = A\omega^2 t</math></center> | ||
| + | |||
| + | e integrando esta ecuación obtenemos el parámetro arco como función del tiempo | ||
| + | |||
| + | <center><math>s = \frac{A\omega^2t^2}{2}</math></center> | ||
| + | |||
==Triedro de Frenet== | ==Triedro de Frenet== | ||
| + | ===Vector tangente=== | ||
| + | Hallamos el vector unitario tangente normalizando la velocidad | ||
| + | |||
| + | <center><math>\vec{T}=\frac{\vec{v}}{v}=\cos(\omega t)\vec{\imath}+\mathrm{sen}(\omega t)\vec{\jmath}</math></center> | ||
| + | |||
| + | Obsérvese que el vector unitario tangente resulta paralelo al vector <math>\overrightarrow{OC}</math> | ||
| + | |||
| + | ===Vector binormal=== | ||
| + | El vector binormal es inmediato. Puesto que la trayectoria está contenida en el plano OXY, el vector binormal será el unitario perpendicular a dicho plano, por lo que <math>\vec{B}=+\vec{k}</math> o <math>\vec{B}=-\vec{k}</math>. El sentido lo da el que debe ser el del producto vectorial de <math>\vec{v}</math> y <math>\vec{a}</math>. Tomando un punto del primer cuadrante la velocidad va hacia Y positiva y la aceleración va hacia donde se curva la trayectoria, por lo que debe ser | ||
| + | |||
| + | <center><math>\vec{B}=\vec{k}</math></center> | ||
| + | |||
| + | ===Vector normal=== | ||
| + | Multiplicando vectorialmente los dos anteriores | ||
| + | |||
| + | <center><math>\vec{N}=\vec{B}\times\vec{T}=-\mathrm{sen}(\omega t)\vec{\imath}+\cos(\omega t)\vec{\jmath}</math></center> | ||
| + | |||
==Radio y centro de curvatura== | ==Radio y centro de curvatura== | ||
| + | Podemos hallar el centro y el radio de curvatura directamente a partir de la velocidad y la aceleración. Sin embargo, es más ilustrativo hallar primero las componentes intrínsecas de la aceleración | ||
| + | |||
| + | No necesitamos proyectar sobre los dos vectores unitarios, nos basta con reconocerlos en la expresión de la aceleración y observar que ésta puede escribirse como | ||
| + | |||
| + | <center><math>\vec{a}(t) =A\omega^2\left(\cos(\omega t)\vec{\imath}+\mathrm{sen}(\omega t)\vec{\jmath}\right)+A\omega^3t\left(-\mathrm{sen}(\omega t)\vec{\imath}+\cos(\omega t)\vec{\jmath}\right) = A\omega^2\vec{T}+A\omega^3t\vec{N}</math></center> | ||
| + | |||
| + | y por tanto | ||
| + | |||
| + | <center><math>a_t = A\omega^2\,</math>{{qquad}}{{qquad}}<math>a_n=A\omega^3t\,</math></center> | ||
| + | |||
| + | Vemos que, dado que la aceleración tangencial es constante, el movimiento es uniformemente acelerado. | ||
| + | |||
| + | El radio de curvatura lo obtenemos de la velocidad y la aceleración normal | ||
| + | |||
| + | <center><math>R = \frac{v^2}{a_n}=\frac{A^2\omega^4t^2}{A\omega^3t}=A\omega t</math></center> | ||
| + | |||
| + | Vemos que va aumentando gradualmente en el tiempo, como corresponde a que la curva es una espiral que se va abriendo. | ||
| + | |||
| + | La posición de los centros de curvatura es | ||
| + | |||
| + | <center><math>\vec{r}_c=\vec{r}+R\vec{N} = A\left(\cos(\omega t)+\omega t\,\mathrm{sen}(\omega t)\right)\vec{\imath}+A\left(\,\mathrm{sen}(\omega t)-\omega t\cos(\omega t)\right)\vec{\jmath}+A\omega t\left(-\mathrm{sen}(\omega t)\vec{\imath}+\cos(\omega t)\vec{\jmath}\right)</math></center> | ||
| + | |||
| + | que nos da | ||
| + | |||
| + | <center><math>\vec{r}_c=A\cos(\omega t)\vec{\imath}+A\,\mathrm{sen}(\omega t)\vec{\jmath}</math></center> | ||
| + | |||
| + | Pero esta es justamente la posición del punto C. Por tanto, el conjunto de los centros de curvatura (lo que se conoce como ''evoluta'') es la propia circunferencia del carrete. | ||
| - | [[Categoría:Problemas de cinemática | + | [[Categoría:Problemas de cinemática del punto material (G.I.T.I.)]] |
última version al 15:19 23 sep 2013
Contenido |
1 Enunciado
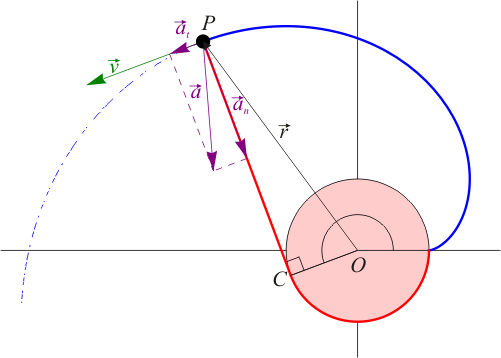
La evolvente de una circunferencia es la curva plana que se obtiene cuando se desenrolla un hilo tenso de un carrete circular. Suponga que se tiene una bobina de radio A que se va desenrollando a ritmo constante, de forma que el punto C donde el hilo deja de hacer contacto con el carrete forma un ángulo θ = ωt con el eje OX. Una partícula material se encuentra en el punto P situado en el extremo del hilo, moviéndose con este extremo a medida que el hilo se va desenrollando.
- Determine el vector de posición de la partícula.
- Calcule la velocidad y la aceleración de la partícula.
- Determine la ley horaria s = s(t).
- Halle los vectores tangente y normal a la trayectoria.
- Halle el radio de curvatura y el centro de curvatura.
2 Vector de posición
Por adición de vectores
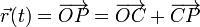
El vector 
es radial y forma un ángulo ωt con el eje OX. Su módulo es A, el radio del carrete:
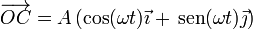
El vector 
es tangente a la circunferencia y por tanto perpendicular al radio. Obtenemos el unitario en esta dirección intercambiando las dos componentes del unitario radial y cambiándole el signo a una de ellas. El sentido lo da el que para ωt < π / 2 la componente X es positiva y la Y es negativa, por tanto
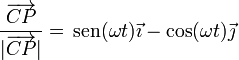
El módulo de 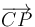lo da la cantidad de hilo desenrollado hasta ese momento, igual al producto del radio por el ángulo, L = Aωt
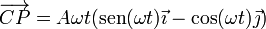
Sumando los dos vectores obtenemos el vector de posición
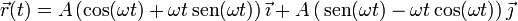
3 Velocidad y aceleración
3.1 Velocidad
Derivando el vector de posición respecto al tiempo obtenemos
3.2 Aceleración
Derivando de nuevo
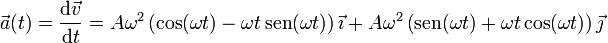
4 Ley horaria
La rapidez con que se recorre la curva la da el módulo de la velocidad
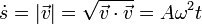
e integrando esta ecuación obtenemos el parámetro arco como función del tiempo
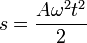
5 Triedro de Frenet
5.1 Vector tangente
Hallamos el vector unitario tangente normalizando la velocidad
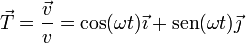
Obsérvese que el vector unitario tangente resulta paralelo al vector
5.2 Vector binormal
El vector binormal es inmediato. Puesto que la trayectoria está contenida en el plano OXY, el vector binormal será el unitario perpendicular a dicho plano, por lo que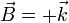 
o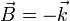 
. El sentido lo da el que debe ser el del producto vectorial de 
y 
. Tomando un punto del primer cuadrante la velocidad va hacia Y positiva y la aceleración va hacia donde se curva la trayectoria, por lo que debe ser
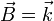
5.3 Vector normal
Multiplicando vectorialmente los dos anteriores
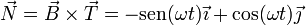
6 Radio y centro de curvatura
Podemos hallar el centro y el radio de curvatura directamente a partir de la velocidad y la aceleración. Sin embargo, es más ilustrativo hallar primero las componentes intrínsecas de la aceleración
No necesitamos proyectar sobre los dos vectores unitarios, nos basta con reconocerlos en la expresión de la aceleración y observar que ésta puede escribirse como
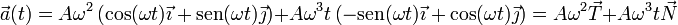
y por tanto
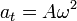
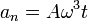
Vemos que, dado que la aceleración tangencial es constante, el movimiento es uniformemente acelerado.
El radio de curvatura lo obtenemos de la velocidad y la aceleración normal
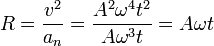
Vemos que va aumentando gradualmente en el tiempo, como corresponde a que la curva es una espiral que se va abriendo.
La posición de los centros de curvatura es
que nos da
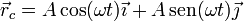
Pero esta es justamente la posición del punto C. Por tanto, el conjunto de los centros de curvatura (lo que se conoce como evoluta) es la propia circunferencia del carrete.
