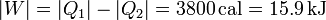Contacto reversible entre dos recipientes
De Laplace
(Página creada con '==Enunciado== Se tienen dos recipientes adiabáticos conteniendo 500 g de agua, a 0°C y 100°C, respectivamente. Se ponen en contacto a través de una pared diate…') |
(→Trabajo realizado) |
||
| (15 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| - | Se tienen dos recipientes adiabáticos | + | Se tienen dos recipientes adiabáticos que contienen 400 y 600 g de agua líquida, respectivamente. La temperatura del primer recipiente es de 0.00 °C y la del segundo 100 °C. |
| - | + | # Los dos recipientes se ponen en contacto térmico a través e una pared diaterma. calcula: | |
| + | ## La temperatura final del agua. | ||
| + | ## Las cantidades de calor transferidas en el proceso. | ||
| + | ## La variación de entropía en el Universo. | ||
| + | # Supón ahora que el contacto térmico no se hace poniendo los sistemas en contacto, sino a través de una máquina térmica reversible que usa los recipientes como foco caliente y frío, de modo que sus temperaturas van cambiando en el tiempo. Si todos los procesos son reversibles… | ||
| + | ## Calcula la temperatura final del agua en este caso. | ||
| + | ## Calcula el calor cedido por el agua caliente y el absorbido por el agua fría. | ||
| + | ## Determina la cantidad de trabajo que se puede extraer del sistema con este procedimiento. | ||
| - | + | ==Temperatura final (irreversible)== | |
| - | + | ||
| - | + | ||
| - | + | [[Archivo:Contacto-dos-recipientes-01.png|right]] | |
| - | + | ||
| - | + | En el estado final la temperatura de ambos recipientes es la misma, T_f. Al estar los recipientes aislados del exterior por paredes adiabáticas, no se intercambia calor con el ambiente. Todo el calor que sale del foco caliente entra en el foco frío. | |
| - | + | Si etiquetamos el sistema más caliente como 1 y el más frío como 2 tenemos que | |
| - | + | <center><math> | |
| + | Q_1 = -Q_2 \qquad\Rightarrow\qquad Q_1+Q_2 = 0</math></center> | ||
| + | |||
| + | Por ser el calor específico del agua prácticamente constante, el calor es proporcional a la variación de temperaturas. Por tanto | ||
| + | |||
| + | <center><math>m_1 c (T_f-T_1) + m_2 c (T_f-T_2)=0\,</math></center> | ||
| + | |||
| + | Despejando de aquí | ||
| + | |||
| + | <center><math>T_f = \frac{m_1 T_1 + m_2 T_2}{m_1+m_2}</math></center> | ||
| + | |||
| + | Sustituyendo los valores numéricos | ||
| + | |||
| + | <center><math>\frac{m_1}{m_1+m_2}=\frac{600}{1000}=\frac{3}{5}</math>{{qquad}}{{qquad}}<math>\frac{m_2}{m_1+m_2}=\frac{400}{1000}=\frac{2}{5}</math>{{qquad}}{{qquad}}<math>T_f = \frac{3\times 100\,^\circ\mathrm{C}}{5}=60\,^\circ\mathrm{C}</math> | ||
| + | </center> | ||
| - | |||
==Calor transferido (irreversible)== | ==Calor transferido (irreversible)== | ||
| - | ==variación de entropía== | + | Conocida la variación de temperaturas, hallamos el calor transferido entre los recipientes de manera inmediata. |
| + | |||
| + | El calor que entra en el agua fría es | ||
| + | |||
| + | <center><math>Q_2 = m_2 c (T_f-T_2) = 400\,\mathrm{g}\times\frac{1\,\mathrm{cal}}{\mathrm{g}\cdot^\circ\mathrm{C}}\times 60\,^\circ \mathrm{C}= 24\,\mathrm{kcal} | ||
| + | </math></center> | ||
| + | |||
| + | El calor que entra en el agua caliente es el mismo, cambiado de signo | ||
| + | |||
| + | <center><math>Q_1 = m_1 c (T_f-T_1) = 600\,\mathrm{g}\times\frac{1\,\mathrm{cal}}{\mathrm{g}\cdot^\circ\mathrm{C}}\times(-40\,^\circ \mathrm{C})= -24\,\mathrm{kcal}</math></center> | ||
| + | |||
| + | Aparte, podría haber transferido entre los recipientes y el entorno, pero al ser adiabáticas las paredes exteriores, este calor es nulo. | ||
| + | |||
| + | ==Producción de entropía== | ||
| + | Este proceso es irreversible, por lo que debe producirse un aumento neto de entropía en el Universo. | ||
| + | |||
| + | Para hallar la variación de entropía en cada recipiente debemos imaginar un proceso reversible que lleve del estado inicial al final. Este proceso reversible consiste en suponer infinitos focos térmicos de temperatura cada vez más baja (para el agua caliente), de forma que el calor intercambiado con cada uno es | ||
| + | |||
| + | <center><math>\mathrm{d}Q_R = m_1 c\,\mathrm{d}T</math></center> | ||
| + | |||
| + | y la variación diferencial de entropía | ||
| + | |||
| + | <center><math>\mathrm{d}S_1 =\frac{\mathrm{d}Q_R}{T}= m_1 c\frac{\mathrm{d}T}{T}</math></center> | ||
| + | |||
| + | La variación total de entropía para el foco caliente es | ||
| + | |||
| + | <center><math>\Delta S_1 = m_1c\int_{T_1}^{T_f} \frac{\mathrm{d}T}{T}=m_1c\ln\left(\frac{T_f}{T_1}\right)</math></center> | ||
| + | |||
| + | puesto que la temperatura final es menor que la inicial, esta variación de entropía es negativa. | ||
| + | |||
| + | La variación de entropía para el foco frío será análogamente | ||
| + | |||
| + | <center><math>\Delta S_2 = m_2c\int_{T_2}^{T_f} \frac{\mathrm{d}T}{T}=m_2c\ln\left(\frac{T_f}{T_2}\right)</math></center> | ||
| + | |||
| + | Sustituyendo los valores numéricos y recordando que es preciso emplear las temperaturas absolutas obtenemos, para el agua caliente | ||
| + | |||
| + | <center><math>\Delta S_1 = 600\,\ln\left(\frac{333}{373}\right)\,\frac{\mathrm{cal}}{\mathrm{K}} =-68.1\,\frac{\mathrm{cal}}{\mathrm{K}}</math></center> | ||
| + | |||
| + | y para la fría | ||
| + | |||
| + | <center><math>\Delta S_2 = 400\,\ln\left(\frac{333}{273}\right)\,\frac{\mathrm{cal}}{\mathrm{K}} =+79.5\,\frac{\mathrm{cal}}{\mathrm{K}}</math></center> | ||
| + | |||
| + | La variación de entropía del agua será la suma de estas dos | ||
| + | |||
| + | <center><math>\Delta S = \Delta S_1 + \Delta S_2 = +11.4\,\frac{\mathrm{cal}}{\mathrm{K}}</math></center> | ||
| + | |||
| + | A esta variación habría que sumar la del entorno, pero, dado que el sistema es adiabático, no hay entrada de calor en el entorno y su variación de entropía es nula. La variación total de entropía es la que acabamos de indicar. Su signo es positivo, como corresponde a un proceso reversible. | ||
| + | |||
==Temperatura final (reversible)== | ==Temperatura final (reversible)== | ||
| - | == | + | |
| + | [[Archivo:Contacto-dos-recipientes-02.png|right]] | ||
| + | |||
| + | Si los recipientes se conectan a través de una máquina térmica, parte del calor que sale del foco caliente se transforma en trabajo y solo un resto va a aparara al agua fría. Por ello, el agua fría se calentará menos que antes y la temperatura final será inferior a la calculada en el primer apartado (aunque en el equilibrio seguirá siendo igual para los dos recipientes). | ||
| + | |||
| + | La forma más sencilla de calcular la nueva temperatura final es observando que, si todos los procesos son reversibles, la variación de entropía es nula, esto es | ||
| + | |||
| + | <center><math>0 = \Delta S = m_1c\ln\left(\frac{T_f}{T_1}\right) + m_2c\ln\left(\frac{T_f}{T_2}\right)</math></center> | ||
| + | |||
| + | En este caso particular, sustituyendo los valores numéricos tenemos | ||
| + | |||
| + | <center><math>600\ln\left(\frac{T_f}{373}\right) + 400\ln\left(\frac{T_f}{273}\right) = 0</math></center> | ||
| + | |||
| + | Simplificando y despejando queda | ||
| + | |||
| + | <center><math>\ln(T_f) = \frac{400\ln(273)+600\ln(373)}{1000} \qquad\Rightarrow\qquad T_f = 329.2\,\mathrm{K}= 56.2\,^\circ\mathrm{C}</math></center> | ||
| + | |||
| + | ==Calores intercambiados (reversibles)== | ||
| + | Conocida la nueva temperatura final, hallamos el calor que entra en cada recipiente de la misma manera que en el caso irreversible. | ||
| + | |||
| + | Para el agua caliente | ||
| + | |||
| + | <center><math>Q_1 = m_1 c(T_f-T_1) = -26280\,\mathrm{cal}</math></center> | ||
| + | |||
| + | y para el agua fría | ||
| + | |||
| + | <center><math>Q_2 = m_2 c(T_f-T_1) = +22480\,\mathrm{cal}</math></center> | ||
| + | |||
| + | Vemos que ahora no coinciden, porque parte del calor que sale del foco frío se va en trabajo. | ||
| + | |||
==Trabajo realizado== | ==Trabajo realizado== | ||
| + | De acuerdo con el primer principio de la termodinámica, el trabajo realizado por la máquina será la diferencia entre el calor que entra en ella y el que se deprende como calor de desecho | ||
| + | |||
| + | <center><math>|W| = |Q_1| - |Q_2| = 3800\,\mathrm{cal} = 15.9\,\mathrm{kJ}</math></center> | ||
| + | |||
| + | [[Categoría:Problemas de Termodinámica]] | ||
| + | [[Categoría:Problemas de examen]] | ||
última version al 11:28 21 sep 2010
Contenido |
1 Enunciado
Se tienen dos recipientes adiabáticos que contienen 400 y 600 g de agua líquida, respectivamente. La temperatura del primer recipiente es de 0.00 °C y la del segundo 100 °C.
- Los dos recipientes se ponen en contacto térmico a través e una pared diaterma. calcula:
- La temperatura final del agua.
- Las cantidades de calor transferidas en el proceso.
- La variación de entropía en el Universo.
- Supón ahora que el contacto térmico no se hace poniendo los sistemas en contacto, sino a través de una máquina térmica reversible que usa los recipientes como foco caliente y frío, de modo que sus temperaturas van cambiando en el tiempo. Si todos los procesos son reversibles…
- Calcula la temperatura final del agua en este caso.
- Calcula el calor cedido por el agua caliente y el absorbido por el agua fría.
- Determina la cantidad de trabajo que se puede extraer del sistema con este procedimiento.
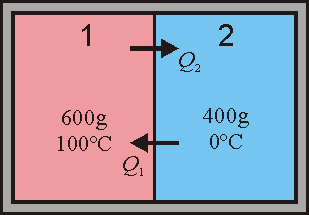
2 Temperatura final (irreversible)
En el estado final la temperatura de ambos recipientes es la misma, T_f. Al estar los recipientes aislados del exterior por paredes adiabáticas, no se intercambia calor con el ambiente. Todo el calor que sale del foco caliente entra en el foco frío. Si etiquetamos el sistema más caliente como 1 y el más frío como 2 tenemos que
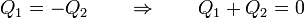
Por ser el calor específico del agua prácticamente constante, el calor es proporcional a la variación de temperaturas. Por tanto
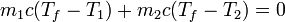
Despejando de aquí
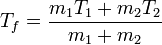
Sustituyendo los valores numéricos
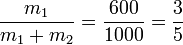
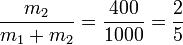
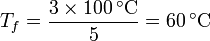
3 Calor transferido (irreversible)
Conocida la variación de temperaturas, hallamos el calor transferido entre los recipientes de manera inmediata.
El calor que entra en el agua fría es
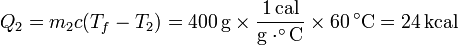
El calor que entra en el agua caliente es el mismo, cambiado de signo
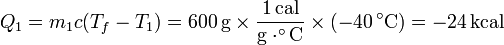
Aparte, podría haber transferido entre los recipientes y el entorno, pero al ser adiabáticas las paredes exteriores, este calor es nulo.
4 Producción de entropía
Este proceso es irreversible, por lo que debe producirse un aumento neto de entropía en el Universo.
Para hallar la variación de entropía en cada recipiente debemos imaginar un proceso reversible que lleve del estado inicial al final. Este proceso reversible consiste en suponer infinitos focos térmicos de temperatura cada vez más baja (para el agua caliente), de forma que el calor intercambiado con cada uno es
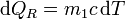
y la variación diferencial de entropía
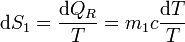
La variación total de entropía para el foco caliente es
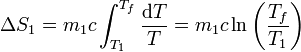
puesto que la temperatura final es menor que la inicial, esta variación de entropía es negativa.
La variación de entropía para el foco frío será análogamente
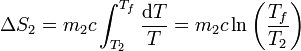
Sustituyendo los valores numéricos y recordando que es preciso emplear las temperaturas absolutas obtenemos, para el agua caliente
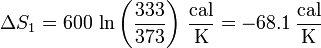
y para la fría
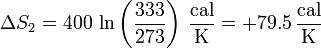
La variación de entropía del agua será la suma de estas dos
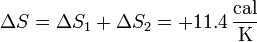
A esta variación habría que sumar la del entorno, pero, dado que el sistema es adiabático, no hay entrada de calor en el entorno y su variación de entropía es nula. La variación total de entropía es la que acabamos de indicar. Su signo es positivo, como corresponde a un proceso reversible.
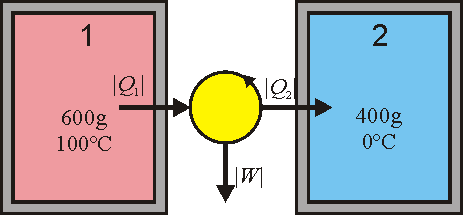
5 Temperatura final (reversible)
Si los recipientes se conectan a través de una máquina térmica, parte del calor que sale del foco caliente se transforma en trabajo y solo un resto va a aparara al agua fría. Por ello, el agua fría se calentará menos que antes y la temperatura final será inferior a la calculada en el primer apartado (aunque en el equilibrio seguirá siendo igual para los dos recipientes).
La forma más sencilla de calcular la nueva temperatura final es observando que, si todos los procesos son reversibles, la variación de entropía es nula, esto es
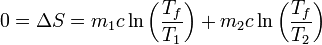
En este caso particular, sustituyendo los valores numéricos tenemos
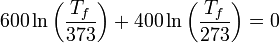
Simplificando y despejando queda
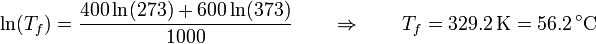
6 Calores intercambiados (reversibles)
Conocida la nueva temperatura final, hallamos el calor que entra en cada recipiente de la misma manera que en el caso irreversible.
Para el agua caliente
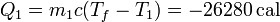
y para el agua fría
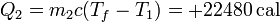
Vemos que ahora no coinciden, porque parte del calor que sale del foco frío se va en trabajo.
7 Trabajo realizado
De acuerdo con el primer principio de la termodinámica, el trabajo realizado por la máquina será la diferencia entre el calor que entra en ella y el que se deprende como calor de desecho