Pistón oscilante
De Laplace
(→Oscilaciones del pistón) |
(→Oscilaciones isotermas del pistón) |
||
| (15 ediciones intermedias no se muestran.) | |||
| Línea 64: | Línea 64: | ||
</center> | </center> | ||
| - | == Oscilaciones del pistón == | + | ==Oscilaciones isotermas del pistón== |
[[Imagen:Piston_oscilante_2.jpg|right]] | [[Imagen:Piston_oscilante_2.jpg|right]] | ||
Partimos ahora de la situación de equilibrio, <math>(P_0,V_0,T)</math> con <math>V_0=Ah_0</math>. Si empujamos ligeramente el | Partimos ahora de la situación de equilibrio, <math>(P_0,V_0,T)</math> con <math>V_0=Ah_0</math>. Si empujamos ligeramente el | ||
| Línea 96: | Línea 96: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \vec{F}=(mg + P_aA-P(x)A)\vec{ | + | \vec{F}=(mg + P_aA-P(x)A)\vec{\imath}=(P_0-P(x))A\vec{\imath}=-(P(x)-P_0)A\vec{\imath} |
</math> | </math> | ||
</center> | </center> | ||
| + | Hemos utilizado la primera ecuación del apartado anterior en la forma | ||
| + | <math>P_oA = P_aA + mg</math>. | ||
Aplicando la Segunda Ley de Newton, encontramos la ecuación diferencial que determina el movimiento del pistón de masa <math>m</math>. | Aplicando la Segunda Ley de Newton, encontramos la ecuación diferencial que determina el movimiento del pistón de masa <math>m</math>. | ||
Como el movimiento es unidimensional prescindimos de los vectores. Tenemos | Como el movimiento es unidimensional prescindimos de los vectores. Tenemos | ||
| Línea 147: | Línea 149: | ||
</center> | </center> | ||
Con los valores del enunciado obtenemos <math>T_{\mathrm{max}}=</math>39.7 K. | Con los valores del enunciado obtenemos <math>T_{\mathrm{max}}=</math>39.7 K. | ||
| + | |||
| + | ==Oscilaciones adiabáticas del pistón== | ||
| + | Si suponemos ahora que el recipiente posee paredes adiabáticas, los cálculos se modifican porque la temperatura no permanece constante. Todo el trabajo que se realiza sobre el sistema se transforma en incremento de energía interna, lo cual conlleva una variación de la temperatura (un incremento, si el trabajo es positivo, y una disminución en caso contrario). | ||
| + | |||
| + | Para la solución en este caso, la ley básica que relaciona los diferentes estados es la ecuación de Poisson | ||
| + | |||
| + | <center><math>PV^\gamma = P_iV_i^\gamma</math></center> | ||
| + | |||
| + | ===Posición de equilibrio=== | ||
| + | Al soltar el pistón, la presión se incrementa hasta que compensa la atmosférica más el peso del émbolo, por lo que | ||
| + | |||
| + | <center><math>P_0(A h)^\gamma = P_a (AH)^\gamma\,</math>{{qquad}}{{qquad}}<math>P_0=P_a+\frac{mg}{A}</math></center> | ||
| + | |||
| + | de donde | ||
| + | |||
| + | <center><math>h_0 = \left(\frac{P_a}{P_0}\right)^{1/\gamma}H=\left(\frac{P_a A}{P_aA+mg}\right)^{1/\gamma} H</math>{{qquad}}</center> | ||
| + | |||
| + | en términos de la temperatura inicial queda | ||
| + | |||
| + | <center><math>P_aAH = n RT\,</math>{{tose}} <math>h_0 = H\left(1+\frac{mgH}{nRT}\right)^{-1/\gamma}</math></center> | ||
| + | |||
| + | ===Frecuencia de oscilación=== | ||
| + | La ecuación de movimiento para el pistón es ahora | ||
| + | |||
| + | <center><math>m\frac{\mathrm{d}^2h}{\mathrm{d}t^2}=-P_aA-mg+PA = -P_aA - mg + \frac{P_aAH^\gamma}{h^\gamma}</math></center> | ||
| + | |||
| + | Escribiendo | ||
| + | |||
| + | <center><math>h = h_0- x \qquad(x\ll h_0)</math></center> | ||
| + | |||
| + | nos queda la ecuación | ||
| + | |||
| + | <center><math>m\frac{\mathrm{d}^2x}{\mathrm{d}t^2}=P_aA+mg-PA = P_aA + mg - P_0A\left(1-\frac{x}{h_0}\right)^{-\gamma}</math></center> | ||
| + | |||
| + | Empleando la aproximación | ||
| + | |||
| + | <center><math>\left(1-\frac{x}{h_0}\right)^{-\gamma}\simeq 1+\frac{\gamma x}{h_0}</math></center> | ||
| + | |||
| + | llegamos a la ecuación del oscilador armónico | ||
| + | |||
| + | <center><math>m\frac{\mathrm{d}^2x}{\mathrm{d}t^2}=-\frac{\gamma P_0A}{h_0}x</math></center> | ||
| + | |||
| + | que nos dcie que la frecuencia de las oscilaciones es ahora | ||
| + | |||
| + | <center><math>\omega = \sqrt{\frac{\gamma P_0A}{mh_0}}</math></center> | ||
| + | |||
| + | Vemos que aparece dentro de la raíz un factor <math>\gamma</math> que no está presente en el caso isotermo. Este factor es el mismo que surge en la expresión para la velocidad del sonido en el aire. En el caso del sonido se trata de oscilaciones rápidas del aire. Aunque no se producen en un sistema aislado, su rapidez hace que el aire no tenga tiempo de intercambiar calor con el aire circundante, por lo que resultan oscilaciones adiabáticas. | ||
| + | |||
| + | Isaac Newton, al tratar de explicar la velocidad del sonido, supuso, erróneamente, que estas oscilaciones eran isotermas, por lo que llegó a un resultado incorrecto (sin el factor <math>\gamma</math> dentro de la raíz), lo que le obligó a hacer trampa y falsear sus resultados y argumentos con tal de hacer coincidir su teoría con la experiencia. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
[[Categoría:Problemas del gas ideal]] | [[Categoría:Problemas del gas ideal]] | ||
[[Categoría:El gas ideal]] | [[Categoría:El gas ideal]] | ||
última version al 14:35 19 may 2010
Contenido |
1 Enunciado
Un cilindro de 2.40 m de altura se llena con 0.100 moles de un gas ideal a una temperatura de 25oC y una presión de 1 bar. El cilindro se cierra entonces con un pistón de masa 1.40 kg que se deja caer hasta alcanzar el equilibrio.
- Determine la altura h0 del pistón suponiendo que la temperatura del gas no varía en la compresión.
- Suponga que el pistón se empuja ligeramente hacia abajo más allá de la posición de equilibrio y luego se libera. Suponiendo que la temperatura del gas permanece constante y que el rozamiento del pistón es despreciable, demuestre que el pistón describe un movimiento armónico simple y determine su frecuencia.
2 Posición de equilibrio
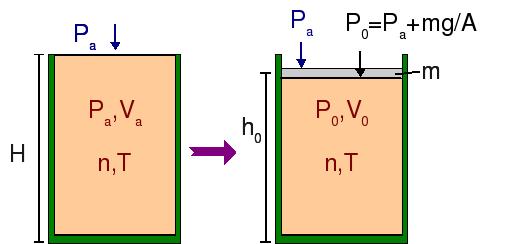
Las condiciones iniciales del gas, antes de colocar el pistón, son (Pa,Va,T), siendo Pa la presión atmosférica, Va = AH el volumen inicial del gas, con A el área de la sección del cilindro, y T = 298.15 K la temperatura que se mantendrá constante durante todo el proceso.
Al colocar el pistón, su peso ejerce una presión añadida al gas, por lo que este se comprime y alcanza un nuevo volumen de equilibrio V0. La presión total sobre el gas en esta situación es
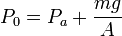
Podemos obtener el valor del área A en función de los datos del problema aplicando la ecuación de estado del gas ideal al estado inicial del gas. Tenemos
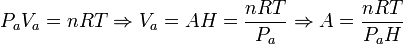
Por tanto, la presión en el estado de equilibrio es
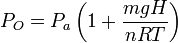
Es interesante analizar el cociente adimensional que ha aparecido en el paréntesis. El numerador es la energía potencial del pistón cuando lo colocamos sobre el gas. El denominador es una energía que está asociada al gas, pues depende de su temperatura. Usando la teoría cinética de los gases puede demostrarse que cada molécula de un gas ideal contribuye con una energía 3kBT / 2 a la energía térmica del gas, siendo kB la constante de Boltzmann. Como hemos visto en teoría, el denominador puede escribirse nRT = NkBT, donde N es el número total de moléculas. En resumen, el cociente puede interpretarse como la importancia relativa de la energía potencial gravitatoria del pistón y la energía térmica asociada al gas. Si la primera es mayor que la segunda, la presión cambia significativamente al añadir el pistón. Si es mucho menor, la presión del gas apenas se ve afectada por la presencia del pistón. En nuestro caso, con los datos del problema tenemos
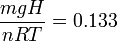
por lo que el valor de la presión de equilibrio cuando está el pistón es
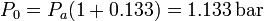
Podemos ahora calcular la altura del pistón en el equilibrio. Como la temperatura es constante en el proceso, los parámetros del estado inicial y el final están relacionados por la ley de Boyle
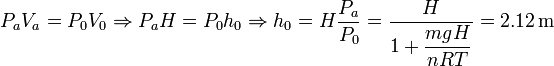
3 Oscilaciones isotermas del pistón
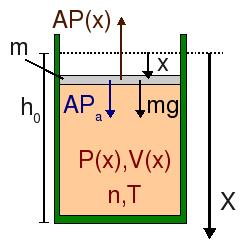
Partimos ahora de la situación de equilibrio, (P0,V0,T) con V0 = Ah0. Si empujamos ligeramente el pistón, aumentamos la presión respecto del valor P0. Escogemos el eje X tal y como se indica en el dibujo. Suponiendo que el proceso es cuasiestático, la presión del gas se adapta en cada instante a la presión ejercida sobre él, de modo que si el pistón se separa una distancia x de su posición de equilibrio, la presión será P = P(x). Podemos determinar esta presión aplicando de nuevo la ley de Boyle entre el estado de equilibrio y el estado en que el pistón ha sido empujado una distancia x
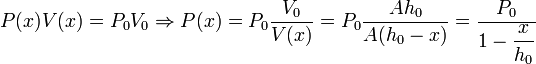
Como empujamos el pistón muy ligeramente, podemos suponer 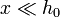 . Usando el desarrollo de Taylor
. Usando el desarrollo de Taylor
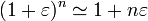
válido cuando 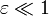 , obtenemos para la presión en función del desplazamiento del pistón
, obtenemos para la presión en función del desplazamiento del pistón
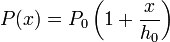
Observamos que si hacemos descender el pistón, la presión del gas es algo mayor que la de equilibrio, mientras que si lo hacemos subir (x < 0), la presión es algo menor. Entonces, si obligamos al pistón a descender y lo soltamos, habrá una fuerza neta sobre el pistón, originada por el desequilibrio entre P0 y P(x). Esta fuerza es, usando el eje X como se indica en la figura
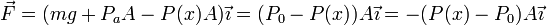
Hemos utilizado la primera ecuación del apartado anterior en la forma PoA = PaA + mg. Aplicando la Segunda Ley de Newton, encontramos la ecuación diferencial que determina el movimiento del pistón de masa m. Como el movimiento es unidimensional prescindimos de los vectores. Tenemos
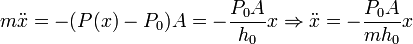
Esta es la ecuación de un movimiento armónico simple con frecuencia angular
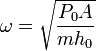
Usando los resultados del apartado anterior, podemos expresar la frecuencia en función de los datos del problema. Obtenemos
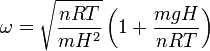
El período de oscilación es
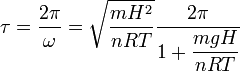
Con los datos del enunciado obtenemos

La gráfica muestra como varía el período con la temperatura para los valores de las magnitudes dados en el enunciado. Para temperaturas altas, el cociente entre energías se hace despreciable, y el período decrece de manera inversamente proporcional a la raíz cuadrada de la temperatura. Para temperaturas bajas, el período alcanza un máximo. La temperatura a la cual ocurre puede encontrarse imponiendo que la derivada del período respecto a T sea nula. Resulta que esta condición se cumple precisamente para la temperatura para la cual el cociente entre energías se hace 1, es decir
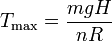
Con los valores del enunciado obtenemos Tmax = 39.7 K.
4 Oscilaciones adiabáticas del pistón
Si suponemos ahora que el recipiente posee paredes adiabáticas, los cálculos se modifican porque la temperatura no permanece constante. Todo el trabajo que se realiza sobre el sistema se transforma en incremento de energía interna, lo cual conlleva una variación de la temperatura (un incremento, si el trabajo es positivo, y una disminución en caso contrario).
Para la solución en este caso, la ley básica que relaciona los diferentes estados es la ecuación de Poisson
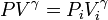
4.1 Posición de equilibrio
Al soltar el pistón, la presión se incrementa hasta que compensa la atmosférica más el peso del émbolo, por lo que
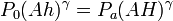
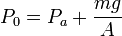
de donde
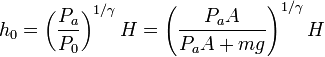
en términos de la temperatura inicial queda
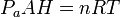

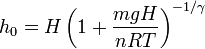
4.2 Frecuencia de oscilación
La ecuación de movimiento para el pistón es ahora
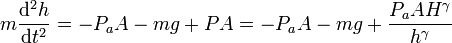
Escribiendo

nos queda la ecuación
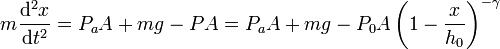
Empleando la aproximación
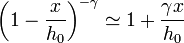
llegamos a la ecuación del oscilador armónico
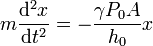
que nos dcie que la frecuencia de las oscilaciones es ahora
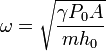
Vemos que aparece dentro de la raíz un factor γ que no está presente en el caso isotermo. Este factor es el mismo que surge en la expresión para la velocidad del sonido en el aire. En el caso del sonido se trata de oscilaciones rápidas del aire. Aunque no se producen en un sistema aislado, su rapidez hace que el aire no tenga tiempo de intercambiar calor con el aire circundante, por lo que resultan oscilaciones adiabáticas.
Isaac Newton, al tratar de explicar la velocidad del sonido, supuso, erróneamente, que estas oscilaciones eran isotermas, por lo que llegó a un resultado incorrecto (sin el factor γ dentro de la raíz), lo que le obligó a hacer trampa y falsear sus resultados y argumentos con tal de hacer coincidir su teoría con la experiencia.