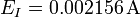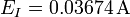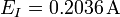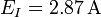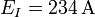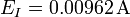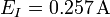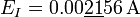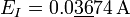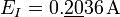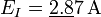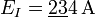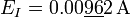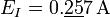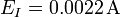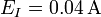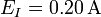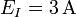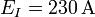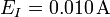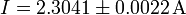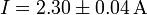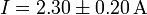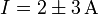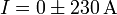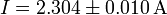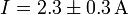Entrar Página Discusión Historial Go to the site toolbox

Expresión de una cantidad con error. Redondeo

De Laplace

(Diferencias entre revisiones)
(Nueva página: ==Introducción== La existencia de una banda de error nos limita el número de cifras significativas que podemos presentar. Por ejemplo, el siguiente resultado sería absurdo: \begin{...)
 
(4 ediciones intermedias no se muestran.)
Línea 1: Línea 1:
==Introducción==
==Introducción==
-
La existencia de una banda de error nos limita el número de cifras significativas que podemos presentar. Por ejemplo, el siguiente
+
La existencia de una [[Incertidumbre_en_los_datos#Bandas de error|banda de error]] nos limita el número de cifras significativas que podemos presentar. Por ejemplo, el siguiente resultado sería absurdo:  
-
resultado sería absurdo: \begin{equation}
+
-
R = 8.4575308\pm 0.2\,\Omega
+
-
\end{equation}
+
-
ya que la banda de error nos dice que el resultado es incierto ya en su
+
-
primera cifra decimal, por lo que dar siete no tiene ningún sentido, ya
+
-
que todo lo que esté más allá de la primera es absolutamente incierto.
+
-
No es que las siguientes cifras sean correctas o incorrectas, es que
+
-
son desconocidas por completo.
+
-
Tampoco tiene mucho sentido excederse en la expresión del error. Por
+
<center><math>R = 8.4575308\pm 0.2\,\Omega</math></center>
-
ejemplo, también sería incorrecta la expresión
+
-
\begin{equation}
+
-
R = 8.4575308\pm 0.2189095\,\Omega
+
-
\end{equation}
+
-
ya que la primera o quizás las dos primeras cifras del error nos dicen
+
-
donde está la incertidumbre. Las cifras sucesivas suponen un
+
-
refinamiento innecesario. Recordemos que el límite del 95\% es
+
-
convencional y no pasa nada si la banda de error delimita una banda del
+
-
94\% o del 96\%.
+
-
Por ello, es importante truncar las expresiones tanto del error como de
+
ya que la banda de error nos dice que el resultado es incierto ya en su primera cifra decimal, por lo que dar siete no tiene ningún sentido, ya que todo lo que esté más allá de la primera es absolutamente incierto. No es que las siguientes cifras sean correctas o incorrectas, es que son desconocidas por completo.
-
la cantidad. Esto requiere una cierta técnica sistemática para
+
-
redondear adecuadamente que consta de los siguientes pasos:
+
-
\punto Se expresa la magnitud objeto de estudio y su error
+
Tampoco tiene mucho sentido excederse en la expresión del error. Por ejemplo, también sería incorrecta la expresión
-
con todas las cifras conocidas.
+
-
\rayas
+
<center><math>R = 8.4575308\pm 0.2189095\,\Omega</math></center>
-
\textbf{Ejemplo:} Supongamos que una medida de una intensidad nos da el
+
ya que la primera o quizás las dos primeras cifras del error nos dicen donde está la incertidumbre. Las cifras sucesivas suponen un
-
valor
+
refinamiento innecesario. Recordemos que la anchura estándar de la banda de error, como aquella en que el resultado tiene un 95% de estar dentro, es convencional y no pasa nada si la banda de error delimita una banda del 94% o del 96%.
-
\begin{equation}
+
-
I=2.30408415\,\mathrm{A}
+
-
\end{equation}
+
-
vamos a ver como se expresa el resultado para seis casos distintos de
+
-
errores de esta cantidad, como pueden ser los siguientes:
+
-
\begin{enumerate}
+
-
\item $E_I=0.002156\,\mathrm{A}$
+
-
\item $E_I=0.03674\,\mathrm{A}$
+
-
\item $E_I=0.2036\,\mathrm{A}$
+
-
\item $E_I=2.87\,\mathrm{A}$
+
-
\item $E_I=234\,\mathrm{A}$
+
-
\item $E_I=0.00962\,\mathrm{A}$
+
-
\item $E_I = 0.257\,\mathrm{A}$
+
-
\end{enumerate}
+
-
\rayai
+
-
\punto Se examinan las dos primeras cifras significativas
+
Por ello, es importante truncar las expresiones tanto del error como de la cantidad. Esto requiere una cierta técnica sistemática para
-
del error (esto es, descontando los ceros situados a la izquierda del
+
redondear adecuadamente que consta de los siguientes pasos:
-
número).
+
-
\rayas
+
==Primer paso==
 +
;Se expresa la magnitud objeto de estudio y su error con todas las cifras conocidas.:
-
\textbf{Ejemplo (cont.):} Para los seis errores anteriores las cifras a
+
'''Ejemplo:''' Supongamos que una medida de una intensidad nos da el valor
-
considerar serán:
+
-
\begin{enumerate}
+
-
\item $E_I=0.00\underline{21}56\,\mathrm{A}$
+
-
\item $E_I=0.0\underline{36}74\,\mathrm{A}$
+
-
\item $E_I=0.\underline{20}36\,\mathrm{A}$
+
-
\item $E_I=\underline{2.8}7\,\mathrm{A}$
+
-
\item $E_I=\underline{23}4\,\mathrm{A}$
+
-
\item $E_I=0.00\underline{96}2\,\mathrm{A}$
+
-
\item $E_I =0.\underline{25}7\,\mathrm{A}$
+
-
\end{enumerate}
+
-
\rayai
+
-
\punto Si el conjunto de las dos cifras seleccionadas es un
+
<center><math>I=2.30408415\,\mathrm{A}</math></center>
-
número menor o igual a $25$, se conservan ambas. Si es un número mayor
+
-
que $25$, se conserva sólo la primera. El resto de las cifras del error
+
-
se elimina. Téngase cuidado de redondear adecuadamente la última cifra
+
-
restante (hacia abajo si lo que viene detrás es menor que 5, hacia
+
-
arriba si es mayor o igual).
+
-
En los ejemplos anteriores, hay un pequeño problema con el último caso.
+
vamos a ver como se expresa el resultado para seis casos distintos de errores de esta cantidad, como pueden ser los siguientes:
-
En principio hay que retener dos cifras (25) pero al redondear el 7
+
-
siguiente nos resulta 26, que obligaría a retener una sola cifra (un 3,
+
-
tras el redondeo del 6). Aunque en los casos límite tampoco es tan
+
-
importante dejar una cifra o dos (ya que el 25 es de nuevo una
+
-
convención), mantendremos el criterio de que realmente se trata de un
+
-
número superior a 25 (sería 25.7) y por tanto se redondea a una sola
+
-
cifra (3).
+
 +
# <math>E_I=0.002156\,\mathrm{A}</math>
 +
# <math>E_I=0.03674\,\mathrm{A}</math>
 +
# <math>E_I=0.2036\,\mathrm{A}</math>
 +
# <math>E_I=2.87\,\mathrm{A}</math>
 +
# <math>E_I=234\,\mathrm{A}</math>
 +
# <math>E_I=0.00962\,\mathrm{A}</math>
 +
# <math>E_I = 0.257\,\mathrm{A}</math>
-
\rayas
+
==Segundo paso==
 +
;Se examinan las dos primeras cifras significativas del error (esto es, descontando los ceros situados a la izquierda del número).
-
\textbf{Ejemplo (cont.):} Esto nos deja con los siguientes errores
+
'''Ejemplo (cont.):''' Para los siete errores anteriores las cifras a considerar serán:
-
\begin{enumerate}
+
-
\item $E_I=0.0022\,\mathrm{A}$
+
-
\item $E_I=0.04\,\mathrm{A}$
+
-
\item $E_I=0.20\,\mathrm{A}$
+
-
\item $E_I=3\,\mathrm{A}$
+
-
\item $E_I=230\,\mathrm{A}$
+
-
\item $E_I=0.010\,\mathrm{A}$
+
-
\item $E_I=0.3\,\mathrm{A}$
+
-
\end{enumerate}
+
-
Obsérvese la diferencia entre colocar un cero de relleno para conservar
+
-
el orden de magnitud correcto (caso (e)) y conservarlos al final cuando
+
-
añaden información (casos (c) y (f))
+
-
\rayai
+
# <math>E_I=0.00\underline{21}56\,\mathrm{A}</math>
 +
# <math>E_I=0.0\underline{36}74\,\mathrm{A}</math>
 +
# <math>E_I=0.\underline{20}36\,\mathrm{A}</math>
 +
# <math>E_I=\underline{2.8}7\,\mathrm{A}</math>
 +
# <math>E_I=\underline{23}4\,\mathrm{A}</math>
 +
# <math>E_I=0.00\underline{96}2\,\mathrm{A}</math>
 +
# <math>E_I =0.\underline{25}7\,\mathrm{A}</math>
-
\punto Ya se ha redondeado el error. Ahora debe redondearse
+
==Tercer paso==
-
la magnitud. Para ello debe verse en qué posición se encuentra la
+
;Si el conjunto de las dos cifras seleccionadas es un número menor o igual a 25, se conservan ambas. Si es un número mayor que 25, se conserva sólo la primera. El resto de las cifras del error se elimina. Téngase cuidado de redondear adecuadamente la última cifra restante (hacia abajo si lo que viene detrás es menor que 5, hacia arriba si es mayor o igual).
-
última cifra del error. Hasta esa misma posición debe retenerse la
+
-
cantidad original. Las cifras siguientes se desprecian, teniendo
+
-
cuidado de redondear la última conservada.
+
 +
En los ejemplos anteriores, hay un pequeño problema con el último caso. En principio hay que retener dos cifras (25) pero al redondear el 7 siguiente nos resulta 26, que obligaría a retener una sola cifra (un 3, tras el redondeo del 6). Aunque en los casos límite tampoco es tan importante dejar una cifra o dos (ya que el 25 es de nuevo una convención), mantendremos el criterio de que realmente se trata de un
 +
número superior a 25 (sería 25.7) y por tanto se redondea a una sola cifra (3).
-
\rayas
+
'''Ejemplo (cont.):''' Esto nos deja con los siguientes errores
 +
#<math>E_I=0.0022\,\mathrm{A}</math>
 +
#<math>E_I=0.04\,\mathrm{A}</math>
 +
#<math>E_I=0.20\,\mathrm{A}</math>
 +
#<math>E_I=3\,\mathrm{A}</math>
 +
#<math>E_I=230\,\mathrm{A}</math>
 +
#<math>E_I=0.010\,\mathrm{A}</math>
 +
#<math>E_I=0.3\,\mathrm{A}</math>
-
\textbf{Ejemplo (cont.):} Para los seis casos anteriores nos quedan las
+
Obsérvese la diferencia entre colocar un cero de relleno para conservar el orden de magnitud correcto (caso (5)) y conservarlos al final cuando añaden información (casos (3) y (6))
-
siguientes expresiones para la intensidad:
+
-
\begin{enumerate}
+
-
\item $I=2.3041\,\mathrm{A}$
+
-
\item $I=2.30\mathrm{A}$
+
-
\item $I=2.30\,\mathrm{A}$
+
-
\item $I=2\,\mathrm{A}$
+
-
\item $I=0\,\mathrm{A}$
+
-
\item $I=2.304\,\mathrm{A}$
+
-
\item $I=2.3\,\mathrm{A}$
+
-
\end{enumerate}
+
-
Nótese cómo de nuevo se conservan los ceros cuando estos son
+
==Cuarto paso==
-
significativos (pues expresan que esa cifra es efectivamente un cero).
+
;Ya se ha redondeado el error. Ahora debe redondearse la magnitud. Para ello debe verse en qué posición se encuentra la última cifra del error. Hasta esa misma posición debe retenerse la cantidad original. Las cifras siguientes se desprecian, teniendo cuidado de redondear la última conservada.
-
En el caso (e), en el cual el error es dos órdenes de magnitud más
+
-
grande que la cantidad, debemos rellenar ésta con ceros a la izquierda
+
-
(como $002.3\ldots\,\mathrm{A}$) y luego redondear las primeras cifras
+
-
(que son nulas) dejando como resultado final un cero.
+
-
\rayai
+
'''Ejemplo (cont.):''' Para los seis casos anteriores nos quedan las siguientes expresiones para la intensidad:
-
\punto Por último, se expresan conjuntamente la cantidad,
+
#<math>I=2.3041\,\mathrm{A}</math>
-
su error y sus unidades.
+
#<math>I=2.30\mathrm{A}</math>
 +
#<math>I=2.30\,\mathrm{A}</math>
 +
#<math>I=2\,\mathrm{A}</math>
 +
#<math>I=0\,\mathrm{A}</math>
 +
#<math>I=2.304\,\mathrm{A}</math>
 +
#<math>I=2.3\,\mathrm{A}</math>
-
\rayas
+
Nótese cómo de nuevo se conservan los ceros cuando estos son significativos (pues expresan que esa cifra es efectivamente un cero). En el caso (5), en el cual el error es dos órdenes de magnitud más grande que la cantidad, debemos rellenar ésta con ceros a la izquierda (como 002.3&hellip;A) y luego redondear las primeras cifras (que son nulas) dejando como resultado final un cero.
-
\textbf{Ejemplo (cont.):} Esto nos da:
+
==Quinto paso==
-
\begin{enumerate}
+
;Por último, se expresan conjuntamente la cantidad, su error y sus unidades.
-
\item $I=2.3041\pm 0.0022\,\mathrm{A}$
+
-
\item $I=2.30\pm 0.04\,\mathrm{A}$
+
-
\item $I=2.30\pm 0.20\,\mathrm{A}$
+
-
\item $I=2\pm 3\,\mathrm{A}$
+
-
\item $I=0\pm 230\,\mathrm{A}$
+
-
\item $I=2.304\pm 0.010\,\mathrm{A}$
+
-
\item $I = 2.3\pm 0.3\,\mathrm{A}$
+
-
\end{enumerate}
+
-
\rayai
+
-
\punto Una presentación alternativa y más compacta consiste en expresar la medida
+
'''Ejemplo (cont.):''' Esto nos da:
-
y, al final, entre paréntesis el error que afecta a la última o últimas
+
-
cifras.
+
 +
# <math>I=2.3041\pm 0.0022\,\mathrm{A}</math>
 +
#<math>I=2.30\pm 0.04\,\mathrm{A}</math>
 +
#<math>I=2.30\pm 0.20\,\mathrm{A}</math>
 +
#<math>I=2\pm 3\,\mathrm{A}</math>
 +
#<math>I=0\pm 230\,\mathrm{A}</math>
 +
#<math>I=2.304\pm 0.010\,\mathrm{A}</math>
 +
#<math>I = 2.3\pm 0.3\,\mathrm{A}</math>
-
\rayas
+
==Expresión compacta==
 +
;Una presentación alternativa y más compacta consiste en expresar la medida y, al final, entre paréntesis el error que afecta a la última o últimas cifras.
-
\textbf{Ejemplo (cont.):} De esta forma quedaría como
+
'''Ejemplo (cont.):''' De esta forma quedaría como  
-
\begin{enumerate}
+
-
\item $I=2.3041(22)\,\mathrm{A}$
+
-
\item $I=2.30(4)\mathrm{A}$
+
-
\item $I=2.30(20)\,\mathrm{A}$
+
-
\item $I=2(3)\,\mathrm{A}$
+
-
\item $I=0(230)\,\mathrm{A}$
+
-
\item $I=2.304(10)\,\mathrm{A}$
+
-
\item $I=2.3(3)\,\mathrm{A}$
+
-
\end{enumerate}
+
-
\rayai
+
-
Estas técnicas deben practicarse hasta que se conviertan en un
+
#<math>I=2.3041(22)\,\mathrm{A}</math>
-
procedimiento automático. No es necesario indicar explícitamente los
+
#<math>I=2.30(4)\mathrm{A}</math>
-
pasos intermedios.
+
#<math>I=2.30(20)\,\mathrm{A}</math>
 +
#<math>I=2(3)\,\mathrm{A}</math>
 +
#<math>I=0(230)\,\mathrm{A}</math>
 +
#<math>I=2.304(10)\,\mathrm{A}</math>
 +
#<math>I=2.3(3)\,\mathrm{A}</math>
-
De todas formas, aunque en los resultados finales las cantidades deben
+
Estas técnicas deben practicarse hasta que se conviertan en un procedimiento automático. No es necesario indicar explícitamente los pasos intermedios.
-
aparecer redondeadas, es conveniente conservar en los borradores las
+
-
cantidades obtenidas, con todas sus cifras, si pretendemos realizar
+
-
algún cálculo posterior con ellas.
+
-
Como regla básica de conducta aplicaremos que los cálculos intermedios
+
De todas formas, aunque en los resultados finales las cantidades deben aparecer redondeadas, es conveniente conservar en los borradores las
-
se hacen con todas las cifras y los resultados finales se presentan
+
cantidades obtenidas, con todas sus cifras, si pretendemos realizar algún cálculo posterior con ellas.
-
redondeados.
+
 
 +
Como regla básica de conducta aplicaremos que los cálculos intermedios se hacen con todas las cifras y los resultados finales se presentan redondeados.
[[Categoría:Prácticas de laboratorio]]
[[Categoría:Prácticas de laboratorio]]

última version al 11:47 18 mar 2010

Contenido

1 Introducción

La existencia de una banda de error nos limita el número de cifras significativas que podemos presentar. Por ejemplo, el siguiente resultado sería absurdo:

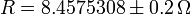
R = 8.4575308\pm 0.2\,\Omega

ya que la banda de error nos dice que el resultado es incierto ya en su primera cifra decimal, por lo que dar siete no tiene ningún sentido, ya que todo lo que esté más allá de la primera es absolutamente incierto. No es que las siguientes cifras sean correctas o incorrectas, es que son desconocidas por completo.

Tampoco tiene mucho sentido excederse en la expresión del error. Por ejemplo, también sería incorrecta la expresión

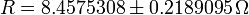
R = 8.4575308\pm 0.2189095\,\Omega

ya que la primera o quizás las dos primeras cifras del error nos dicen donde está la incertidumbre. Las cifras sucesivas suponen un refinamiento innecesario. Recordemos que la anchura estándar de la banda de error, como aquella en que el resultado tiene un 95% de estar dentro, es convencional y no pasa nada si la banda de error delimita una banda del 94% o del 96%.

Por ello, es importante truncar las expresiones tanto del error como de la cantidad. Esto requiere una cierta técnica sistemática para redondear adecuadamente que consta de los siguientes pasos:

2 Primer paso

Se expresa la magnitud objeto de estudio y su error con todas las cifras conocidas.

Ejemplo: Supongamos que una medida de una intensidad nos da el valor

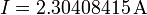
I=2.30408415\,\mathrm{A}

vamos a ver como se expresa el resultado para seis casos distintos de errores de esta cantidad, como pueden ser los siguientes:

  1. E_I=0.002156\,\mathrm{A}
  2. E_I=0.03674\,\mathrm{A}
  3. E_I=0.2036\,\mathrm{A}
  4. E_I=2.87\,\mathrm{A}
  5. E_I=234\,\mathrm{A}
  6. E_I=0.00962\,\mathrm{A}
  7. E_I = 0.257\,\mathrm{A}

3 Segundo paso

Se examinan las dos primeras cifras significativas del error (esto es, descontando los ceros situados a la izquierda del número).

Ejemplo (cont.): Para los siete errores anteriores las cifras a considerar serán:

  1. E_I=0.00\underline{21}56\,\mathrm{A}
  2. E_I=0.0\underline{36}74\,\mathrm{A}
  3. E_I=0.\underline{20}36\,\mathrm{A}
  4. E_I=\underline{2.8}7\,\mathrm{A}
  5. E_I=\underline{23}4\,\mathrm{A}
  6. E_I=0.00\underline{96}2\,\mathrm{A}
  7. E_I =0.\underline{25}7\,\mathrm{A}

4 Tercer paso

Si el conjunto de las dos cifras seleccionadas es un número menor o igual a 25, se conservan ambas. Si es un número mayor que 25, se conserva sólo la primera. El resto de las cifras del error se elimina. Téngase cuidado de redondear adecuadamente la última cifra restante (hacia abajo si lo que viene detrás es menor que 5, hacia arriba si es mayor o igual).

En los ejemplos anteriores, hay un pequeño problema con el último caso. En principio hay que retener dos cifras (25) pero al redondear el 7 siguiente nos resulta 26, que obligaría a retener una sola cifra (un 3, tras el redondeo del 6). Aunque en los casos límite tampoco es tan importante dejar una cifra o dos (ya que el 25 es de nuevo una convención), mantendremos el criterio de que realmente se trata de un número superior a 25 (sería 25.7) y por tanto se redondea a una sola cifra (3).

Ejemplo (cont.): Esto nos deja con los siguientes errores

  1. E_I=0.0022\,\mathrm{A}
  2. E_I=0.04\,\mathrm{A}
  3. E_I=0.20\,\mathrm{A}
  4. E_I=3\,\mathrm{A}
  5. E_I=230\,\mathrm{A}
  6. E_I=0.010\,\mathrm{A}
  7. E_I=0.3\,\mathrm{A}

Obsérvese la diferencia entre colocar un cero de relleno para conservar el orden de magnitud correcto (caso (5)) y conservarlos al final cuando añaden información (casos (3) y (6))

5 Cuarto paso

Ya se ha redondeado el error. Ahora debe redondearse la magnitud. Para ello debe verse en qué posición se encuentra la última cifra del error. Hasta esa misma posición debe retenerse la cantidad original. Las cifras siguientes se desprecian, teniendo cuidado de redondear la última conservada.

Ejemplo (cont.): Para los seis casos anteriores nos quedan las siguientes expresiones para la intensidad:

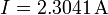
  1. I=2.3041\,\mathrm{A}
  2. I = 2.30A
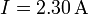
  3. I=2.30\,\mathrm{A}
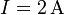
  4. I=2\,\mathrm{A}
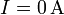
  5. I=0\,\mathrm{A}
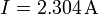
  6. I=2.304\,\mathrm{A}
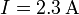
  7. I=2.3\,\mathrm{A}

Nótese cómo de nuevo se conservan los ceros cuando estos son significativos (pues expresan que esa cifra es efectivamente un cero). En el caso (5), en el cual el error es dos órdenes de magnitud más grande que la cantidad, debemos rellenar ésta con ceros a la izquierda (como 002.3…A) y luego redondear las primeras cifras (que son nulas) dejando como resultado final un cero.

6 Quinto paso

Por último, se expresan conjuntamente la cantidad, su error y sus unidades.

Ejemplo (cont.): Esto nos da:

  1. I=2.3041\pm 0.0022\,\mathrm{A}
  2. I=2.30\pm 0.04\,\mathrm{A}
  3. I=2.30\pm 0.20\,\mathrm{A}
  4. I=2\pm 3\,\mathrm{A}
  5. I=0\pm 230\,\mathrm{A}
  6. I=2.304\pm 0.010\,\mathrm{A}
  7. I = 2.3\pm 0.3\,\mathrm{A}

7 Expresión compacta

Una presentación alternativa y más compacta consiste en expresar la medida y, al final, entre paréntesis el error que afecta a la última o últimas cifras.

Ejemplo (cont.): De esta forma quedaría como

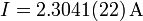
  1. I=2.3041(22)\,\mathrm{A}
  2. I = 2.30(4)A
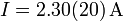
  3. I=2.30(20)\,\mathrm{A}
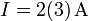
  4. I=2(3)\,\mathrm{A}
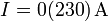
  5. I=0(230)\,\mathrm{A}
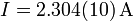
  6. I=2.304(10)\,\mathrm{A}
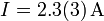
  7. I=2.3(3)\,\mathrm{A}

Estas técnicas deben practicarse hasta que se conviertan en un procedimiento automático. No es necesario indicar explícitamente los pasos intermedios.

De todas formas, aunque en los resultados finales las cantidades deben aparecer redondeadas, es conveniente conservar en los borradores las cantidades obtenidas, con todas sus cifras, si pretendemos realizar algún cálculo posterior con ellas.

Como regla básica de conducta aplicaremos que los cálculos intermedios se hacen con todas las cifras y los resultados finales se presentan redondeados.

Obtenido de "http://tesla.us.es/wiki/index.php/Expresi%C3%B3n_de_una_cantidad_con_error._Redondeo"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 11:47, 18 mar 2010. - Esta página ha sido visitada 21.600 veces. - Aviso legal - Acerca de Laplace