Masa puntual con muelle y varilla

De Laplace

(Diferencias entre revisiones)

última version al 15:41 25 ene 2010

Contenido

1 Enunciado
2 Solución

1 Enunciado

Una masa puntual $m$ se halla ensartada en una varilla $\overline{AB}$ apoyada en una esquina como se ve en la figura. La varilla está fijada a la pared y al suelo de modo que no se mueve. La masa puede moverse sin rozamiento bajo la acción del peso y de un resorte de longitud natural nula y constante recuperadora $k$ , cuyos extremos están conectados a la partícula material y a un punto del eje vertical que en cada instante se halla a la misma altura que la partícula.

Determine cuál es el valor de $x$ para el que la partícula se encuentra en equilibrio mecánico. ¿Qué relación debe cumplirse entre los parámetros del problema para que esta situación sea posible?
Obtenga las expresiones de las energías potenciales gravitatoria y del muelle en función de $x$ .
Obtenga la expresión de la energía cinética y de la energía mecánica de la partícula para una posición arbitraria sobre la varilla.
Determine entre qué posiciones se moverá la partícula cuando es abandonada, en reposo, en el extremo superior de la varilla ( $A$ ). ¿Cuál es la condición que debe cumplirse para que este movimiento sea posible? Compárela con la condición encontrada en el primer apartado.

2 Solución

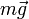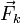La figura de al lado muestra las fuerzas que actúan sobre la masa, a saber: el peso , $m\vec{g}$ , la fuerza recuperadora del muelle, $\vec{F}_k$ , y la normal ejercida por la barra, $\vec{N}$ . Como el contacto es liso, ésta última es normal a la barra, como se indica en la figura. Usando el triedro $O X Y$ propuesto, estas fuerzas se expresan como

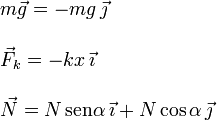
$\begin{array}{l} m\vec{g} = -mg\,\vec{\jmath}\\ \\ \vec{F}_k=-kx\,\vec{\imath}\\ \\ \vec{N} = N\,\mathrm{sen}\alpha\,\vec{\imath}+N\cos\alpha\,\vec{\jmath} \end{array}$

La posición de equilibrio $x eq$ se determina imponiendo que la suma de fuerzas sobre la partícula sea nula. Tenemos

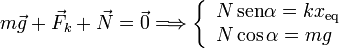
$m\vec{g}+\vec{F}_k+\vec{N}=\vec{0}\Longrightarrow \left\{ \begin{array}{l} N\,\mathrm{sen}\alpha=kx_{\mathrm{eq}}\\N\cos\alpha=mg \end{array} \right.$

Dividendo las dos ecuaciones entre sí obtenemos el valor de $x eq$

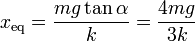
$x_{\mathrm{eq}}=\dfrac{mg\tan\alpha}{k}=\dfrac{4mg}{3k}$

De la figura se observa que $tanα = (4 a / 3 a) = 4 / 3$ .

Para que la partícula pueda alcanzar esta posición debe ocurrir que

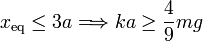
$x_{\mathrm{eq}}\leq 3a \Longrightarrow ka\geq\dfrac{4}{9}mg$

Físicamente, esto quiere decir que si la masa es demasiado grande, o el muelle demasiado débil, o la varilla demasiado corta, la fuerza del muelle no es suficiente para compensar el peso de la partícula. Si se diera este caso, al llegar al punto $B$ intervendría la reacción del suelo para hacer que la partícula permaneciese en reposo.

2.1 Energía potencial

La partícula está sometida a la fuerza gravitatoria y a la del muelle. Las dos son conservativas, y tienen asociada una energía potencial. Como la longitud natural del muelle es nula, la energía potencial elástica es

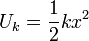
$U_k=\dfrac{1}{2}kx^2$

pues la elongación del muelle es $x$ . Para la gravitatoria, escogemos como origen de energías $y = 0$ . Entonces la energía potencial es

$U g = m g y$

Podemos expresar la coordenada $y$ de la partícula en función de $x$ usando la ecuación de la recta definida por la varilla. Tenemos

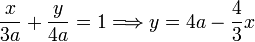
$\dfrac{x}{3a} + \dfrac{y}{4a} = 1 \Longrightarrow y = 4a-\dfrac{4}{3}x$

Con esto obtenemos

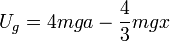
$U_g = 4mga-\dfrac{4}{3}mgx$

2.2 Energía cinética y mecánica

La energía cinética de la partícula es

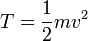
$T = \dfrac{1}{2}mv^2$

Para calcular la velocidad derivamos respecto al tiempo el vector de posición

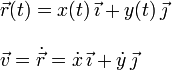
$\begin{array}{l} \vec{r}(t) = x(t)\,\vec{\imath}+y(t)\,\vec{\jmath}\\ \\ \vec{v} = \dot{\vec{r}} = \dot{x}\,\vec{\imath}+\dot{y}\,\vec{\jmath} \end{array}$

A partir de la expresión de $y$ en función de $x$ vemos que

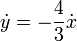
$\dot{y} = -\dfrac{4}{3}\dot{x}$

Entonces

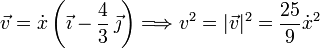
$\vec{v} = \dot{x}\left(\vec{\imath}-\dfrac{4}{3}\,\vec{\jmath}\right) \Longrightarrow v^2=|\vec{v}|^2=\dfrac{25}{9}\dot{x}^2$

La energía cinética es

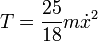
$T = \dfrac{25}{18}m\dot{x}^2$

Y la energía mecánica es la suma de las energías cinética y potencial, es decir

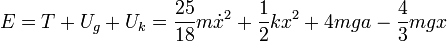
$E = T+U_g+U_k = \dfrac{25}{18}m\dot{x}^2 + \dfrac{1}{2}kx^2+ 4mga-\dfrac{4}{3}mgx$

2.3 Posición inicial en 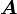$\boldsymbol{A}$

Si colocamos la partícula inicialmente en reposo en $A$ , la fuerza ejercida por el muelle es nula. Entonces la componente de la gravedad paralela a la barra hace que comience a descender por ella. Según aumenta $x$ , el muelle tira de ella con más fuerza, y la componente de la fuerza elástica paralela a la barra se opone a la acción de la gravedad, de modo que puede llegar frenar a la partícula. En este momento se alcanzaría un punto de retorno, y la partícula volvería a deslizarse hacia arriba.

Para encontrar este punto de retorno, utilizamos el hecho de que la energía mecánica se conserva, pues las dos fuerzas que actúan son conservativas. En el instante inicial, la velocidad es cero y $x = 0$ . Por tanto, en este movimiento la energía mecánica vale

$E = E (x = 0) = 4 m g a$

Introduciendo este valor en la expresión de la energía mecánica obtenemos

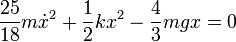
$\dfrac{25}{18}m\dot{x}^2 + \dfrac{1}{2}kx^2-\dfrac{4}{3}mgx=0$

Los puntos de retorno corresponden a los puntos en que la velocidad es cero, es decir $\dot{x}=0$ . Imponiendo esta condición obtenemos la ecuación de segundo grado

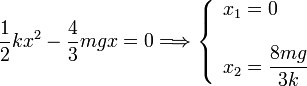
$\dfrac{1}{2}kx^2-\dfrac{4}{3}mgx=0\Longrightarrow \left\{ \begin{array}{l} x_1 = 0\\ \\ x_2 = \dfrac{8mg}{3k} \end{array} \right.$

La primera solución es el punto de partida, la segunda es el punto de retorno.

Para que esta oscilación sea posible, la partícula no debe pasar del punto $B$ , pues entonces intervendría la reacción normal del suelo. Así pues la condición que debe cumplirse es

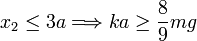
$x_2\leq 3a\Longrightarrow ka\geq\dfrac{8}{9}mg$

Es interesante señalar que esta condición exige que el muelle sea dos veces más fuerte que la obtenida para el equilibrio en el primer apartado. En el primer apartado, la condición es que la fuerza del muelle equilibre a la de la gravedad. En el movimiento de este apartado, cuando se llega a la posición de equilibrio, la aceleración de la partícula es nula, pero en ese instante tiene una velocidad distinta de cero. Es el muelle el que debe frenarla, y por eso debe ser más fuerte (o la barra más larga).

@@ Línea 203: / Línea 203: @@
 que debe frenarla, y por eso debe ser más fuerte (o la barra más larga).
-[[Categoria:Problemas de examen]]
+[[Categoría:Problemas de examen]]
-[[Categoria:Problemas de Estática:]]
+[[Categoría: Problemas de Estática]]
+[[Categoría: Problemas Física Aeronáuticos]]

Masa puntual con muelle y varilla

De Laplace

última version al 15:41 25 ene 2010

Contenido

1 Enunciado

2 Solución

2.1 Energía potencial

2.2 Energía cinética y mecánica

2.3 Posición inicial en $\boldsymbol{A}$

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES