Coeficientes de capacidad
De Laplace
(→Problema del potencial) |
(→Problema del potencial) |
||
| Línea 1: | Línea 1: | ||
==Problema del potencial== | ==Problema del potencial== | ||
{{ac|Problema del potencial}} | {{ac|Problema del potencial}} | ||
| + | Cuando se tiene un sistema de conductores <math>S_k</math> a diferentes potenciales <math>V_k</math>, y quiere determinarse la distribución de potencial eléctrico y de campo eléctrico entre ellos, debe resolverse el [[problema del potencial]]: | ||
| + | |||
| + | <math>\nabla^2\phi = 0</math> | ||
| + | |||
| + | con las condiciones de contorno | ||
| + | |||
| + | <center><math>\phi = V_k\quad (\mathbf{r}\in S_k)</math>{{qquad}}{{qquad}}<math>\phi\to 0\quad (r\to\infty)</math></center> | ||
| + | |||
| + | Suponemos que la única carga se encuentra sobre los conductores, y no en el espacio entre ellos; por ello, la ecuación diferencial es la de Laplace y no la de Poisson. La condición de contorno en el infinito puede ser sustituida por una en una superficie exterior que rodee al sistema (porque tengamos, por ejemplo, un sistema de conductores dentro de una [[jaula de Faraday]]). | ||
| + | |||
| + | La solución de este problema permite hallar el campo eléctrico entre los conductores, la carga en cada conductor, y la energía almacenada, entre otras cantidades. Aunque puede demostrarse que existe solución y es única, ello no quiere decir que sea sencilla de calcular. En muy pocos casos existe solución analítica y a menudo es preciso recurrir a una solución numérica. | ||
==Solución del problema del potencial== | ==Solución del problema del potencial== | ||
Revisión de 21:04 11 ene 2010
Contenido |
1 Problema del potencial
Cuando se tiene un sistema de conductores Sk a diferentes potenciales Vk, y quiere determinarse la distribución de potencial eléctrico y de campo eléctrico entre ellos, debe resolverse el problema del potencial:

con las condiciones de contorno
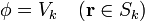
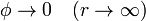
Suponemos que la única carga se encuentra sobre los conductores, y no en el espacio entre ellos; por ello, la ecuación diferencial es la de Laplace y no la de Poisson. La condición de contorno en el infinito puede ser sustituida por una en una superficie exterior que rodee al sistema (porque tengamos, por ejemplo, un sistema de conductores dentro de una jaula de Faraday).
La solución de este problema permite hallar el campo eléctrico entre los conductores, la carga en cada conductor, y la energía almacenada, entre otras cantidades. Aunque puede demostrarse que existe solución y es única, ello no quiere decir que sea sencilla de calcular. En muy pocos casos existe solución analítica y a menudo es preciso recurrir a una solución numérica.





