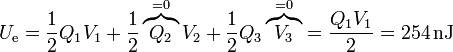Sistema de cuatro conductores prismáticos
De Laplace
(→Carga en cada conductor) |
(→Cargas y potenciales) |
||
| (16 ediciones intermedias no se muestran.) | |||
| Línea 8: | Línea 8: | ||
# Si el conductor 1 se encuentra a tensión <math>V_1=100\,\mathrm{V}</math>, el 2 aislado y descargado y el 3 a tierra, ¿cuáles son las cargas y los potenciales de los tres conductores? ¿Y la energía electrostática almacenada en el sistema? | # Si el conductor 1 se encuentra a tensión <math>V_1=100\,\mathrm{V}</math>, el 2 aislado y descargado y el 3 a tierra, ¿cuáles son las cargas y los potenciales de los tres conductores? ¿Y la energía electrostática almacenada en el sistema? | ||
| - | + | ==Carga en cada conductor== | |
| - | + | ||
Lo que se pide en este apartado es hallar la carga en cada conductor conocidas las tensiones de cada uno. Para calcularlas necesitamos los coeficientes de capacidad, que relacionan ambas magnitudes en forma matricial | Lo que se pide en este apartado es hallar la carga en cada conductor conocidas las tensiones de cada uno. Para calcularlas necesitamos los coeficientes de capacidad, que relacionan ambas magnitudes en forma matricial | ||
| Línea 16: | Línea 15: | ||
En este caso tenemos realmente cuatro conductores, contando el exterior, pero dado que este rodea a los otros tres y se encuentra permanentemente a tierra, puede ser tratado como el infinito, y no incluirse en los cálculos explícitamente. | En este caso tenemos realmente cuatro conductores, contando el exterior, pero dado que este rodea a los otros tres y se encuentra permanentemente a tierra, puede ser tratado como el infinito, y no incluirse en los cálculos explícitamente. | ||
| - | La forma más rápida de hallar los coeficientes de capacidad en este problema es mediante un circuito equivalente | + | La forma más rápida de hallar los coeficientes de capacidad en este problema es mediante un circuito equivalente. |
| - | + | En primer lugar colocamos un nodo por cada conductor, lo cual nos da tres nodos, más la referencia de tierra. | |
| - | + | ||
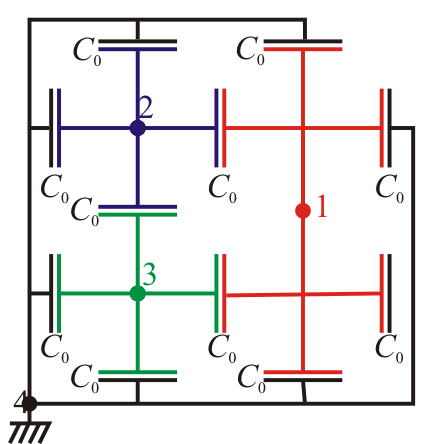
| - | [[Categoría:Problemas de | + | [[Imagen:prismas02.gif|right]]A continuación colocamos un condensador entre cada par de nodos. Estos condensadores representan la contribución de las líneas de campo que van de un conductor a otro. Dadas las dimensiones de los bloques, podemos aproximar estos condensadores por unos de placas planas y paralelas, despreciando los efectos de borde en las esquinas de cada prisma. Sea |
| + | |||
| + | <center><math>b = 20\,\mathrm{mm}</math>{{qquad}}<math>L = 50\,\mathrm{mm}</math>{{qquad}}<math>a =1\,\mathrm{mm}</math></center> | ||
| + | |||
| + | entonces los condensadores que el conductor 1 forma con el 2 y el 3 son iguales entre sí y a | ||
| + | |||
| + | <center><math>\overline{C}_{12}=\overline{C}_{13}=\frac{\varepsilon_0bL}{a}\equiv C_0 \simeq 8.85\,\mathrm{pF}</math></center> | ||
| + | |||
| + | El que forma el 2 con el 3 tiene también el mismo valor | ||
| + | |||
| + | <center><math>\overline{C}_{23}=\frac{\varepsilon_0bL}{a}= C_0</math></center> | ||
| + | |||
| + | Ahora hay que añadir los condensadores que cada conductor forma con la tierra del sistema. Para los conductores 2 y 3 este condensador es aproximadamente igual a dos condensadores <math>C_0</math> puestos en paralelo, mientras que para el conductor 1 la capacidad es aproximadamente igual a <math>4C_0</math>, esto es | ||
| + | |||
| + | <center> | ||
| + | <math>\overline{C}_{22}=\overline{C}_{33}\simeq 2C_0</math>{{qquad}}<math>\overline{C}_{11}\simeq4C_0</math></center> | ||
| + | |||
| + | Por tanto, la carga en cada nodo será igual a | ||
| + | |||
| + | <center><math>Q_1 = \overline{C}_{11}V_1+\overline{C}_{12}(V_1-V_2)+\overline{C}_{13}(V_1-V_3) = C_0(6V_1-V_2-V_3)</math>{{qquad}} | ||
| + | <math>Q_2 = \overline{C}_{22}V_2+\overline{C}_{12}(V_2-V_1)+\overline{C}_{23}(V_2-V_3) = C_0(-V_1+4V_2-V_3)</math>{{qquad}} | ||
| + | <math>Q_3 = \overline{C}_{33}V_3+\overline{C}_{13}(V_3-V_1)+\overline{C}_{23}(V_3-V_2) = C_0(-V_1-V_2+4V_3)</math></center> | ||
| + | |||
| + | o, en forma matricial, | ||
| + | |||
| + | <center><math>\begin{pmatrix}Q_1 \\ Q_2 \\ Q_3\end{pmatrix} = C_0\begin{pmatrix}6 & -1 & -1\\ -1 & 4 & -1 \\ -1 & -1 & 4\end{pmatrix}\cdot \begin{pmatrix}V_1 \\ V_2 \\ V_3\end{pmatrix}</math></center> | ||
| + | |||
| + | Para hallar las cargas en cada conductor, basta sustituir ahora las tensiones de cada uno. | ||
| + | |||
| + | <center><math>\begin{pmatrix}Q_1 \\ Q_2 \\ Q_3\end{pmatrix} = 8.85\begin{pmatrix}6 & -1 & -1\\ -1 & 4 & -1 \\ -1 & -1 & 4\end{pmatrix}\cdot \begin{pmatrix}10 \\ 20 \\ -10\end{pmatrix}\,\mathrm{pC}=\begin{pmatrix}0.44 \\ 0.71 \\ -0.62\end{pmatrix}\,\mathrm{nC}</math></center> | ||
| + | |||
| + | La carga en el conductor interior será igual a la suma de los tres interiores, cambiada de signo | ||
| + | |||
| + | <center><math>Q_4=-Q_1-Q_2-Q_3 = -0.53\,\mathrm{nC}</math></center> | ||
| + | |||
| + | ==Energía almacenada== | ||
| + | Una vez que conocemos las cargas y los potenciales de cada conductor, tenemos la energía | ||
| + | |||
| + | <center><math>U_\mathrm{e}=\frac{1}{2}\begin{pmatrix}Q_1 & Q_2 & Q_3\end{pmatrix}\cdot\begin{pmatrix}V_1\\ V_2\\V_3\end{pmatrix} = \frac{1}{2}\begin{pmatrix}0.44 & 0.71 & -0.62\end{pmatrix}\cdot\begin{pmatrix}10\\ 20\\-10\end{pmatrix}=12\,\mathrm{nJ}</math></center> | ||
| + | |||
| + | Si empleamos sólo el vector de los potenciales el cálculo es | ||
| + | |||
| + | <center><math>U_\mathrm{e}=\frac{C_0}{2}\begin{pmatrix}V_1 & V_2 & V_3\end{pmatrix}\cdot\begin{pmatrix}6 & -1 & -1\\ -1 & 4 & -1 \\ -1 & -1 & 4\end{pmatrix}\cdot\begin{pmatrix}V_1\\ V_2\\V_3\end{pmatrix}=\frac{C_0}{2}\left(6V_1^2-2V_1V_2-2V_1V_3+4V_2^2-2V_2V_3+4V_3^2\right)</math></center> | ||
| + | |||
| + | Si usamos el circuito equivalente será | ||
| + | |||
| + | <center><math>U_\mathrm{e}=\frac{1}{2}\left(4C_0V_1^2+2C_0V_2^2+2C_0V_3^2 +C_0(V_1-V_2)^2 + C_0(V_1-V_3)^2+C_0(V_2-V_3)^2\right)</math></center> | ||
| + | |||
| + | ==Cargas y potenciales== | ||
| + | Si lo que nos dan son los datos | ||
| + | |||
| + | <center><math>V_1=100\,\mathrm{V}</math>{{qquad}}{{qquad}}<math>Q_2=0\,\mathrm{V}</math>{{qquad}}{{qquad}}<math>V_3=0\,\mathrm{V}</math></center> | ||
| + | |||
| + | debemos despejar el resto de las incógnitas: <math>Q_1</math>, <math>V_2</math> y <math>Q_3</math>. Para la segunda tenemos | ||
| + | |||
| + | <center><math>0 = Q_2 = C_0(-V_1+4V_2-V_3)\,</math>{{tose}}<math>V_2 = \frac{V_1+V_3}{4}=25\,\mathrm{V}</math></center> | ||
| + | |||
| + | Una vez conocidas las tres tensiones, hallamos las cargas como antes | ||
| + | |||
| + | <center><math>\begin{pmatrix}Q_1 \\ Q_2 \\ Q_3\end{pmatrix} = 8.85\begin{pmatrix}6 & -1 & -1\\ -1 & 4 & -1 \\ -1 & -1 & 4\end{pmatrix}\cdot \begin{pmatrix}100 \\ 25 \\ 0\end{pmatrix}\,\mathrm{pC}=\begin{pmatrix}5.09 \\ 0.00 \\ -1.11\end{pmatrix}\,\mathrm{nC}</math></center> | ||
| + | |||
| + | La nueva energía es simplemente | ||
| + | |||
| + | <center><math>U_\mathrm{e}=\frac{1}{2}Q_1V_1 +\frac{1}{2}\overbrace{Q_2}^{=0}V_2+\frac{1}{2}Q_3\overbrace{V_3}^{=0}=\frac{Q_1V_1}{2} = 254\,\mathrm{nJ}</math></center> | ||
| + | |||
| + | [[Categoría:Problemas de electrostática en presencia de conductores]] | ||
última version al 20:38 10 ene 2010
Contenido |
1 Enunciado
Se tiene un sistema de cuatro conductores tal como se indica en la figura. Uno de ellos (conductor “4”) es un prisma cuadrado hueco de lado 43 mm y longitud 50 mm. Este conductor se encuentra siempre a tierra.En su interior se encuentran tres conductores. El conductor “1” es un paralelepípedo de lados 41 mm, 20 mm y 50 mm. Los conductores “2” y “3” son sendos prismas cuadrados de lado 20 mm y altura 50 mm. la distancia entre superficies conductoras vecinas es de 1 mm.
- Teniendo en cuenta la pequeñez relativa de las diferentes distancias calcule, aproximadamente, las cargas que almacenan los conductores 1, 2 y 3, cuando sus tensiones son
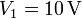 ,
, 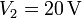 y
y 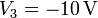 .
.
- Para la configuración anterior, calcule la energía electrostática almacenada en el sistema.
- Si el conductor 1 se encuentra a tensión
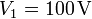 , el 2 aislado y descargado y el 3 a tierra, ¿cuáles son las cargas y los potenciales de los tres conductores? ¿Y la energía electrostática almacenada en el sistema?
, el 2 aislado y descargado y el 3 a tierra, ¿cuáles son las cargas y los potenciales de los tres conductores? ¿Y la energía electrostática almacenada en el sistema?
2 Carga en cada conductor
Lo que se pide en este apartado es hallar la carga en cada conductor conocidas las tensiones de cada uno. Para calcularlas necesitamos los coeficientes de capacidad, que relacionan ambas magnitudes en forma matricial
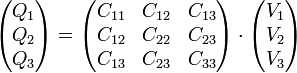
En este caso tenemos realmente cuatro conductores, contando el exterior, pero dado que este rodea a los otros tres y se encuentra permanentemente a tierra, puede ser tratado como el infinito, y no incluirse en los cálculos explícitamente.
La forma más rápida de hallar los coeficientes de capacidad en este problema es mediante un circuito equivalente.
En primer lugar colocamos un nodo por cada conductor, lo cual nos da tres nodos, más la referencia de tierra.
A continuación colocamos un condensador entre cada par de nodos. Estos condensadores representan la contribución de las líneas de campo que van de un conductor a otro. Dadas las dimensiones de los bloques, podemos aproximar estos condensadores por unos de placas planas y paralelas, despreciando los efectos de borde en las esquinas de cada prisma. Sea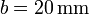
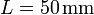
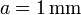
entonces los condensadores que el conductor 1 forma con el 2 y el 3 son iguales entre sí y a
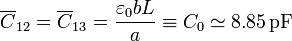
El que forma el 2 con el 3 tiene también el mismo valor
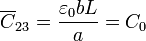
Ahora hay que añadir los condensadores que cada conductor forma con la tierra del sistema. Para los conductores 2 y 3 este condensador es aproximadamente igual a dos condensadores C0 puestos en paralelo, mientras que para el conductor 1 la capacidad es aproximadamente igual a 4C0, esto es
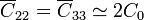
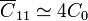
Por tanto, la carga en cada nodo será igual a

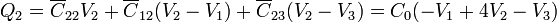
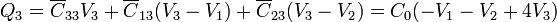
o, en forma matricial,
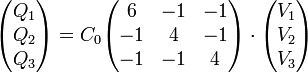
Para hallar las cargas en cada conductor, basta sustituir ahora las tensiones de cada uno.

La carga en el conductor interior será igual a la suma de los tres interiores, cambiada de signo
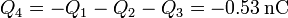
3 Energía almacenada
Una vez que conocemos las cargas y los potenciales de cada conductor, tenemos la energía
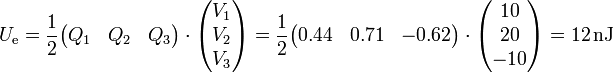
Si empleamos sólo el vector de los potenciales el cálculo es
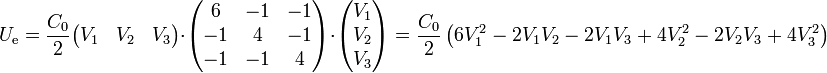
Si usamos el circuito equivalente será
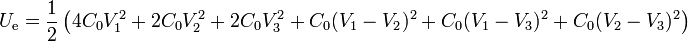
4 Cargas y potenciales
Si lo que nos dan son los datos
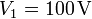
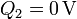
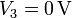
debemos despejar el resto de las incógnitas: Q1, V2 y Q3. Para la segunda tenemos


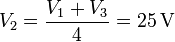
Una vez conocidas las tres tensiones, hallamos las cargas como antes
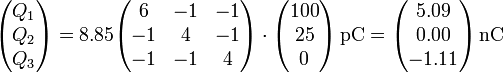
La nueva energía es simplemente