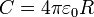Coeficientes de capacidad
De Laplace
(Diferencias entre revisiones)
(Nueva página: Si no hay densidad de carga volumétrica, las cargas almacenadas en los distintos conductores forman una combinación lineal de los potenciales respectivos <center><math>Q_i = \sum_j...) |
(→Capacidad de un conductor) |
||
| Línea 27: | Línea 27: | ||
<center><math>C = 4\pi\varepsilon_0 R</math></center> | <center><math>C = 4\pi\varepsilon_0 R</math></center> | ||
| - | [[Categoría: | + | [[Categoría:Campo eléctrico en presencia de conductores]] |
Revisión de 19:23 10 ene 2010
Si no hay densidad de carga volumétrica, las cargas almacenadas en los distintos conductores forman una combinación lineal de los potenciales respectivos
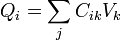
siendo los Cik los coeficientes de capacidad.
Estas relaciones pueden expresarse en forma matricial
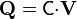
siendo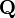 
y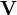 
dos vectores columna y 
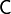una matriz cuadrada simétrica y definida positiva.
Los coeficientes de capacidad verifican
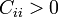
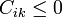
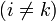
Capacidad de un conductor
Artículo completo: Capacidad de un conductor
En el caso particular de un solo conductor, la expresión se reduce a
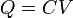
con C la capacidad del conductor, medida en faradios (F). Como caso particular, para una esfera de radio R
