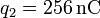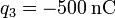Cuatro cargas en un rectángulo

De Laplace

Revisión de 14:02 8 ene 2010 (ver código fuente) Antonio (Discusión | contribuciones) (→Enunciado) ← Edición más antigua		última version al 18:50 8 ene 2010 (ver código fuente) Antonio (Discusión | contribuciones) (→Solución)
(10 ediciones intermedias no se muestran.)
Línea 6:		Línea 6:
	==Solución==		==Solución==
		+	La fuerza sobre la carga <math>q_4</math> es, de acuerdo con la ley de Coulomb y el principio de superposición
		+
		+	<center><math>\mathbf{F}_4 = \frac{q_4}{4\pi\varepsilon_0}\left(\frac{q_1(\mathbf{r}_4-\mathbf{r}_1)}{|\mathbf{r}_4-\mathbf{r}_1|^3}+\frac{q_2(\mathbf{r}_4-\mathbf{r}_2)}{|\mathbf{r}_4-\mathbf{r}_2|^3}+\frac{q_3(\mathbf{r}_4-\mathbf{r}_3)}{|\mathbf{r}_4-\mathbf{r}_3|^3}\right)</math></center>
		+
		+	En nuestro caso, midiendo las distancias en milímetros, tenemos que
		+
		+	<center><math>
		+	\mathbf{r}_1=\mathbf{0}\,</math>{{qquad}}{{qquad}}<math>\mathbf{r}_2=25\,\mathbf{u}_x</math>{{qquad}}{{qquad}}<math>\mathbf{r}_3=16\mathbf{u}_x+12\mathbf{u}_y\,</math>{{qquad}}{{qquad}}<math>\mathbf{r}_4=9\mathbf{u}_x-12\mathbf{u}_y</math></center>
		+
		+	[[Imagen:4cargasrejilla.gif|right]]La posición relativa de <math>q_4</math> respecto a las otras tres cargas y las distancias correspondientes son
		+
		+	;De <math>q_4</math> a <math>q_1</math>
		+	<center><math>\mathbf{r}_4-\mathbf{r}_1 = 9\mathbf{u}_x-12\mathbf{u}_y</math>{{tose}}<math>\left|\mathbf{r}_4-\mathbf{r}_1\right| = \sqrt{9^2+12^2}=15</math></center>
		+	;De <math>q_4</math> a <math>q_2</math>
		+	<center><math>\mathbf{r}_4-\mathbf{r}_2 = -16\mathbf{u}_x-12\mathbf{u}_y</math>{{tose}}<math>\left|\mathbf{r}_4-\mathbf{r}_2\right| = \sqrt{16^2+12^2}=20</math></center>
		+
		+	;De <math>q_4</math> a <math>q_3</math>
		+	<center><math>\mathbf{r}_4-\mathbf{r}_3 = -7\mathbf{u}_x-24\mathbf{u}_y</math>{{tose}}<math>\left|\mathbf{r}_4-\mathbf{r}_3\right| = \sqrt{7^2+24^2}=25</math></center>
		+
		+	Por tanto, la fuerza sobre <math>q_4</math> es, midiendo las cargas en nanoculombios y las distancias en milímetros,
		+
		+	<center><math>\mathbf{F}_4=\frac{q_4}{4\pi\varepsilon_0}\left(\frac{108(9\mathbf{u}_x-12\mathbf{u}_y)}{15^3}+\frac{q_2(-16\mathbf{u}_x-12\mathbf{u}_y)}{20^3}+\frac{q_3(-7\mathbf{u}_x-24\mathbf{u}_y)}{25^3}\right)</math></center>
		+
		+	Para que esta fuerza sea nula debe serlo cada una de sus componentes, lo que nos da las ecuaciones
		+
		+	<center><math>0=\frac{36}{25}-\frac{q_2}{500}-\frac{7q_3}{15625}</math>{{qquad}}{{qquad}}<math>0=-\frac{48}{125}-\frac{3q_2}{2000}-\frac{24q_3}{15625}</math></center>
		+
		+	cuya solución es
		+
		+	<center><math>q_2= 256\,\mathrm{nC}</math>{{qquad}}{{qquad}}<math>q_3=-500\,\mathrm{nC}</math></center>
		+
		+
	[[Categoría:Problemas de electrostática en el vacío]]		[[Categoría:Problemas de electrostática en el vacío]]

---

última version al 18:50 8 ene 2010

1 Enunciado

Una carga puntual 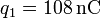se encuentra situada en el origen de coordenadas. En 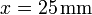, 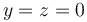se halla una segunda carga q₂. En 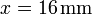, 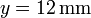se encuentra una tercera carga q₃.

Calcule el valor que deben tener q₂ y q₃ si, ocupando las posiciones indicadas, se desea que sea nula la fuerza sobre una carga 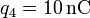situada en 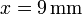, , 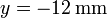z = 0.

2 Solución

La fuerza sobre la carga q₄ es, de acuerdo con la ley de Coulomb y el principio de superposición

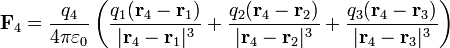
En nuestro caso, midiendo las distancias en milímetros, tenemos que

                         La posición relativa de q₄ respecto a las otras tres cargas y las distancias correspondientes son

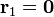
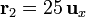
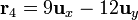
De q₄ a q₁

      

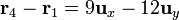
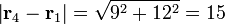
De q₄ a q₂

      

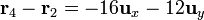
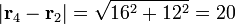
De q₄ a q₃

      

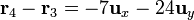
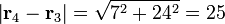
Por tanto, la fuerza sobre q₄ es, midiendo las cargas en nanoculombios y las distancias en milímetros,

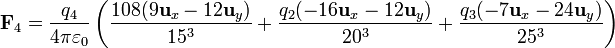
Para que esta fuerza sea nula debe serlo cada una de sus componentes, lo que nos da las ecuaciones

        

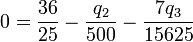
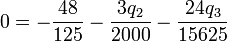
cuya solución es