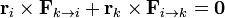Sistemas de partículas
De Laplace
(→Definición de sistema de partículas) |
(→Definición de sistema de partículas) |
||
| Línea 23: | Línea 23: | ||
En la mayoría de los casos se cumplirá además que la fuerza que la partícula <math>k</math> ejerce sobre la <math>i</math> (y por tanto la que la <math>i</math> ejerce sobre la <math>k</math>) va en la dirección de la recta que une ambas partículas. Matemáticamente, esto se expresa imponiendo que el vector <math>\mathbf{F}_{k\to i}</math> es paralelo a la posición relativa <math>\mathbf{r}_i-\mathbf{r}_k</math>, esto es, si | En la mayoría de los casos se cumplirá además que la fuerza que la partícula <math>k</math> ejerce sobre la <math>i</math> (y por tanto la que la <math>i</math> ejerce sobre la <math>k</math>) va en la dirección de la recta que une ambas partículas. Matemáticamente, esto se expresa imponiendo que el vector <math>\mathbf{F}_{k\to i}</math> es paralelo a la posición relativa <math>\mathbf{r}_i-\mathbf{r}_k</math>, esto es, si | ||
| - | <center><math>(\mathbf{r} | + | <center><math>(\mathbf{r}_{i}-\mathbf{r}_k)\times\mathbf{F}_{k\to i} = \mathbf{0}</math></center> |
Eliminando paréntesis y aplicando la tercera ley de Newton esto equivale a la condición | Eliminando paréntesis y aplicando la tercera ley de Newton esto equivale a la condición | ||
Revisión de 21:15 12 dic 2009
Contenido |
1 Definición de sistema de partículas
En mecánica consideramos un sistema de partículas como un conjunto de N puntos materiales que se mueven por separado, si bien interactúan entre sí y están sometidos a fuerzas externas.
Cada una de las partículas del sistema posee una masa propia, mi, siendo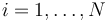 
un índice que sirve para etiquetar individualmente cada una de las partículas. la partícula i está caracterizada por una posición 
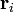y una velocidad 
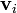. Esta posición y esta velocidad evolucionan de acurdo con las leyes de la dinámica
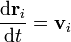
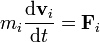
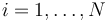
siendo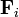 
la resultante de las fuerzas que actúan sobre la partícula i. Esta resultante se compone de las fuerzas que cada una de las demás partículas del sistema ejerce sobre i, más la resultante de las fuerzas externas aplicadas sobre ella
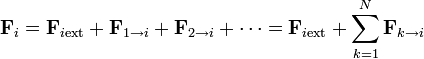
Este sumatorio representa la suma sobre las partículas restantes, esto es k va de 1 hasta N, excluyendo el caso k = i, ya que admitimos que una partícula no produce fuerza sobre sí misma (equivalentemente,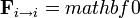 
).
Suponemos que las interacciones entre las partículas obdecen la 3ª ley de Newton
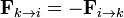
o, lo que es lo mismo
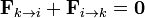
En la mayoría de los casos se cumplirá además que la fuerza que la partícula k ejerce sobre la i (y por tanto la que la i ejerce sobre la k) va en la dirección de la recta que une ambas partículas. Matemáticamente, esto se expresa imponiendo que el vector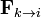 
es paralelo a la posición relativa 
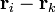, esto es, si
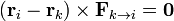
Eliminando paréntesis y aplicando la tercera ley de Newton esto equivale a la condición
