Imán en forma de tubo
De Laplace
(Diferencias entre revisiones)
(→Corrientes de volumen) |
|||
| Línea 16: | Línea 16: | ||
Esta densidad es nula tanto en el exterior del imán (porque fuera la magnetización es nula), como en su interior (porque es uniforme) | Esta densidad es nula tanto en el exterior del imán (porque fuera la magnetización es nula), como en su interior (porque es uniforme) | ||
| - | <center><math>\mathbf{J}_m = \nabla\times\mathbf{M}=\begin{cases}\nabla\times\mathbf{M}_0=\mathbf{0} & \mathrm{interior}\\ \nabla\times\mathbf{0}=\mathbf{0} & \mathrm{exterior}</math></center> | + | <center><math>\mathbf{J}_m = \nabla\times\mathbf{M}=\begin{cases}\nabla\times\mathbf{M}_0=\mathbf{0} & \mathrm{interior}\\ \nabla\times\mathbf{0}=\mathbf{0} & \mathrm{exterior}\end{cases}</math></center> |
Por tanto las únicas densidades de corriente serán superficiales. | Por tanto las únicas densidades de corriente serán superficiales. | ||
Revisión de 16:34 10 sep 2009
Contenido |
1 Enunciado
Se tiene un tubo cilíndrico imanado longitudinalmente con una magnetización uniforme 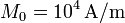 . El tubo posee una longitud
. El tubo posee una longitud  , un radio interior
, un radio interior  y uno exterior
y uno exterior 
- Calcule las corrientes de imanación equivalentes a este imán.
- Halle las cargas de imanación equivalentes.
- Calcule el valor exacto del campo magnético en el centro del tubo.
- Halle el momento dipolar del imán y calcule el valor aproximado del campo magnético en un punto situado a 10 cm en la dirección del eje.
2 Corrientes de imanación
Las corrientes de imanación equivalentes a la magnetización pueden ser volumétricas y superficiales.
2.1 Corrientes de volumen
La densidad de volumétrica de corrientes de magnetización es

Esta densidad es nula tanto en el exterior del imán (porque fuera la magnetización es nula), como en su interior (porque es uniforme)

Por tanto las únicas densidades de corriente serán superficiales.





