Entrar Página Discusión Historial Go to the site toolbox

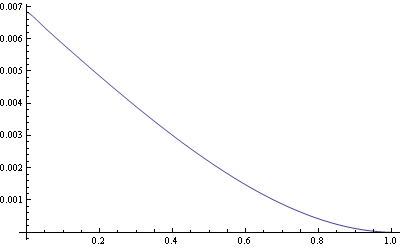
Problema de capa límite

De Laplace

(Diferencias entre revisiones)
(→Enunciado)
(→La solución ingenua)
 
(12 ediciones intermedias no se muestran.)
Línea 18: Línea 18:
cuya solución es de la forma
cuya solución es de la forma
-
<center><math>y = a \exp\left((-\frac{x^2}{2}\right)</math></center>
+
<center><math>y = a \exp\left(-\frac{x^2}{2}\right)</math></center>
pero rápidamente tropezamos con un problema: tenemos una sola constante de integración, <math>a</math>, y dos condiciones de contorno. No podemos satisfacer ambas a la vez. Como mucho una.
pero rápidamente tropezamos con un problema: tenemos una sola constante de integración, <math>a</math>, y dos condiciones de contorno. No podemos satisfacer ambas a la vez. Como mucho una.
Línea 24: Línea 24:
¿Cuál de las dos? Es fácil ver que si imponemos <math>y(0) = 0</math> nos quedamos sin nada, así que esa es la problemática. Sí podemos imponer la otra,  
¿Cuál de las dos? Es fácil ver que si imponemos <math>y(0) = 0</math> nos quedamos sin nada, así que esa es la problemática. Sí podemos imponer la otra,  
-
<center><math>1 = a \exp\left(-\frac{1}{2}\right)</math>{{tose}}<math>a = \sqrt{e}</math></center>
+
<center><math>1 = a \exp\left(-\frac{1}{2}\right)</math>{{tose}}<math>a = \sqrt{\mathrm{e}}</math></center>
así que aproximamos la solución por
así que aproximamos la solución por
-
<center><math>y = \sqrt(e)\exp\left(-\frac{x^2}{2}\right)</math></center>
+
<center><math>y = \sqrt{\mathrm{e}}\exp\left(-\frac{x^2}{2}\right)</math></center>
-
Pero es claro que esta solución no vale cerca de <math>x=0</math>, pues ahí vale <math>\sqrt{e}</math> y debería valer 0. Cerca de <math>x=0</math> la solución debe variar muy rápidamente para poder satisfacer la condición de contorno
+
Pero es claro que esta solución no vale cerca de <math>x=0</math>, pues ahí vale <math>\sqrt{\mathrm{e}}</math> y debería valer 0. Cerca de <math>x=0</math> la solución debe variar muy rápidamente para poder satisfacer la condición de contorno
Estamos en un caso de ''perturbaciones singulares''. Si existe una zona en la que la solución varía muy rápidamente, como aquí cerca de x=0, la segunda derivada será muy grande y el término que hemos despreciado no será pequeño.
Estamos en un caso de ''perturbaciones singulares''. Si existe una zona en la que la solución varía muy rápidamente, como aquí cerca de x=0, la segunda derivada será muy grande y el término que hemos despreciado no será pequeño.
Línea 39: Línea 39:
Veamos como podemos estudiar el comportamiento cerca de <math>x=0</math>. Necesitamos una lupa, que en este caso es un reescalado. Definamos una nueva variable <math>X</math>, que es finita en la región <math>x \ll 1</math>, como
Veamos como podemos estudiar el comportamiento cerca de <math>x=0</math>. Necesitamos una lupa, que en este caso es un reescalado. Definamos una nueva variable <math>X</math>, que es finita en la región <math>x \ll 1</math>, como
-
<math>X = \frac{x}{\delta}</math>
+
<center><math>X = \frac{x}{\delta}</math></center>
-
con delta otro parámetro pequeño que hay que determinar. Si escribimos la ecuación diferencial en términos de X queda
+
con <math>\delta</math> otro parámetro pequeño que hay que determinar. Si escribimos la ecuación diferencial en términos de <math>X</math> queda
-
eps/delta^2 Y'' + Y'/delta + delta X Y = 0
+
<center><math> \frac{\varepsilon}{\delta^2}\frac{\mathrm{d}^2Y}{\mathrm{d}X^2} + \frac{1}{\delta}\frac{\mathrm{d}Y}{\mathrm{d}X} + \delta X Y = 0</math></center>
-
el valor de delta lo sacamos de que al menos dos de los términos sean del mismo orden, lo que en este caso nos da delta = eps y nos deja con
+
el valor de <math>\delta</math> lo sacamos de que al menos dos de los términos sean del mismo orden, lo que en este caso nos da  
-
Y'' + Y' + eps^2 X Y = 0
+
<center><math>\delta = \varepsilon</math></center>
 +
 
 +
y nos deja con
 +
 
 +
<center><math>\frac{\mathrm{d}^2Y}{\mathrm{d}X^2} + \frac{\mathrm{d}Y}{\mathrm{d}X} + \varepsilon^2 X Y = 0</math></center>
despreciando ahora el último término, que es mucho más pequeño, nos quedamos con la ecuación diferencial
despreciando ahora el último término, que es mucho más pequeño, nos quedamos con la ecuación diferencial
-
Y'' + Y' = 0     ---> Y = A + B exp(-X)
+
<center><math>\frac{\mathrm{d}^2Y}{\mathrm{d}X^2} + \frac{\mathrm{d}Y}{\mathrm{d}X}  = 0</math>{{tose}}<math>Y = A + B \exp\left(-X\right)</math></center>
-
Ahora sí podemos imponer la condición en x=0 y escribir la solución interior como
+
Ahora sí podemos imponer la condición en <math>x=0</math> y escribir la solución interior como
-
Y = A(1 - exp(-X))
+
<center><math>Y = A(1 - \exp(-X))\,</math></center>
Pero ¿cuánto vale A?
Pero ¿cuánto vale A?
-
4) El 'matching'
+
==El ''matching''==
Para poder hallar A debemos empalmar la solución interior con la exterior. Esto se hace imponiendo que sobre una escala intermedia entre x y X (mucho menor que x pero mucho mayor que X) ambas soluciones coincidan. En su versión más sencilla, se impone que el comportamiento, para x pequeño de la solución exterior coincida con el comportamiento, para X grande, de la solución interior, esto es,
Para poder hallar A debemos empalmar la solución interior con la exterior. Esto se hace imponiendo que sobre una escala intermedia entre x y X (mucho menor que x pero mucho mayor que X) ambas soluciones coincidan. En su versión más sencilla, se impone que el comportamiento, para x pequeño de la solución exterior coincida con el comportamiento, para X grande, de la solución interior, esto es,
-
lim_(x->0) y = lim_(X->oo) Y
+
<center><math>\lim_{x\to 0} y = \lim_{X\to\infty} Y</math></center>
lo que nos da
lo que nos da
-
rq(e) = A
+
<center><math>\sqrt{\mathrm{e}} = A\,</math></center>
y por tanto la solución interior es
y por tanto la solución interior es
-
Y = rq(e)(1-exp(-X)) = rq(e)(1-exp(-X/eps))
+
<center><math>Y = \sqrt{\mathrm{e}}\left(1-\exp(-X)\right) = \sqrt{\mathrm{e}}\left(1-\exp\left(-\frac{x}{\varepsilon}\right)\right)</math></center>
 +
 
 +
==La solución uniforme==
 +
 
 +
Tenemos entonces dos aproximaciones para la solución de la ecuación diferencial. Una que vale siempre que <math>x</math> no sea muy pequeño
 +
 
 +
<center><math>y = \sqrt{\mathrm{e}}\exp\left(-\frac{x^2}{2}\right)</math></center>
 +
 
 +
y una que vale cuando <math>x</math> es muy pequeño (de orden <math>\varepsilon</math> o menor)
 +
 
 +
<center><math>Y = \sqrt{\mathrm{e}}\left(1-\exp\left(-\frac{x}{\varepsilon}\right)\right)</math></center>
 +
 
 +
¿Cómo podemos conseguir una solución aproximada para todo el intervalo? Recordemos el límite común de ambas funciones. Esto quiere decir que para x pequeño la solución exterior vale <math>L = \sqrt{\mathrm{e}}</math> y para <math>x</math> finito la exterior vale lo mismo. Esto nos permite construir una solución uniforme sumando ambas y restando el límite común
 +
 
 +
<center><math>y_u(x) = y + Y - L = \sqrt{\mathrm{e}}\left(\exp\left(-\frac{x^2}{2}\right) - \exp\left(-\frac{x}{\varepsilon}\right)\right)</math></center>
 +
 
 +
Esta es la solución que andábamos buscando. No cumple la ecuación diferencial en ningún punto, pero se diferencia de la solución en un término del orden de <math>\varepsilon</math> en todo el intervalo (de hecho, el error máximo es menor que el 1% en todo el intervalo.
 +
 
 +
==Algunas gráficas==
 +
* La solución calculada numéricamente
 +
 
 +
<center>[[Imagen:gexacta.gif]]</center>
 +
 
 +
* Las soluciones interior y exterior
-
5) La solución uniforme
+
<center>[[Imagen:gio.gif]]</center>
-
Tenemos entonces dos aproximaciones para la solución de la ecuación diferencial. Una que vale siempre que x no sea muy pequeño
+
* La exacta y las dos aproximadas
-
y = rq(e)exp(-x^2/2)
+
<center>[[Imagen:geio.gif]]</center>
-
y una que vale cuando x es muy pequeño
+
* La exacta y la solución uniforme
-
Y = rq(e)(1-exp(-x/eps))
+
<center>[[Imagen:geu.gif]]</center>
-
¿Cómo podemos conseguir una solución aproximada para todo el intervalo? Recordemos el límite común de ambas funciones. Esto quiere decir que para x pequeño la solución exterior vale L = rq(e) y para x finito la exterior vale lo mismo. Esto nos permite construir una solución uniforme sumando ambas y restando el límite común
+
* Error absoluto en el intervalo
-
y_u(x) = y + Y - L = rq(e)(exp(-x^2/2) - exp(-x/eps))
+
<center>[[Imagen:eabs.gif]]</center>
-
Esta es la solución que andábamos buscando. No cumple la ecuación diferencial en ningún punto, pero se diferencia de la solución en un término del orden de eps en todo el intervalo (de hecho, el error máximo es menor que el 1% en todo el intervalo.
+
* Error relativo en todo el intervalo
-
Algunas gráficas:
+
<center>[[Imagen:erel.gif]]</center>

última version al 13:02 15 ago 2009

Contenido

1 Enunciado

Obtener una solución aproximada, con un error máximo de un 1% en todo el intervalo (0,1) para la ecuación diferencial

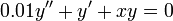
0.01y'' + y' + x y = 0\,        y(0) = 0\,        y(1) = 1\,

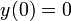
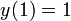
2 Generalizamos el problema

En vez de hacerlo para el caso particular de 1% de error y con un coeficiente 0.01, vamos a suponer un parámetro pequeño eps y estudiamos la ecuación diferencial

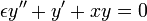
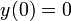\epsilon y'' + y' + x y = 0\,        y(0) = 0\,        y(1) = 1

y queremos hallar una solución aproximada con un error de orden \varepsilon.

3 La solución ingenua

Como primera aproximación, si toleramos un error de orden eps, despreciamos el primer término y nos quedamos con

y' + xy = 0\,

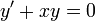
cuya solución es de la forma

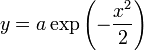
y = a \exp\left(-\frac{x^2}{2}\right)

pero rápidamente tropezamos con un problema: tenemos una sola constante de integración, a, y dos condiciones de contorno. No podemos satisfacer ambas a la vez. Como mucho una.

¿Cuál de las dos? Es fácil ver que si imponemos y(0) = 0 nos quedamos sin nada, así que esa es la problemática. Sí podemos imponer la otra,

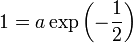
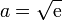
1 = a \exp\left(-\frac{1}{2}\right)   \Rightarrow   a = \sqrt{\mathrm{e}}

así que aproximamos la solución por

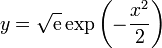
y = \sqrt{\mathrm{e}}\exp\left(-\frac{x^2}{2}\right)

Pero es claro que esta solución no vale cerca de x = 0, pues ahí vale 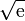\sqrt{\mathrm{e}} y debería valer 0. Cerca de x = 0 la solución debe variar muy rápidamente para poder satisfacer la condición de contorno

Estamos en un caso de perturbaciones singulares. Si existe una zona en la que la solución varía muy rápidamente, como aquí cerca de x=0, la segunda derivada será muy grande y el término que hemos despreciado no será pequeño.

Lo que hemos hallado es realmente la solución exterior, que vale fuera de esta zona de cambio rápido (la capa límite), pero no dentro de ella.

4 Solución interior

Veamos como podemos estudiar el comportamiento cerca de x = 0. Necesitamos una lupa, que en este caso es un reescalado. Definamos una nueva variable X, que es finita en la región 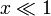x \ll 1, como

X = \frac{x}{\delta}

con δ otro parámetro pequeño que hay que determinar. Si escribimos la ecuación diferencial en términos de X queda

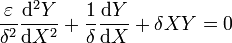
\frac{\varepsilon}{\delta^2}\frac{\mathrm{d}^2Y}{\mathrm{d}X^2} + \frac{1}{\delta}\frac{\mathrm{d}Y}{\mathrm{d}X} + \delta X Y = 0

el valor de δ lo sacamos de que al menos dos de los términos sean del mismo orden, lo que en este caso nos da

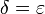
\delta = \varepsilon

y nos deja con

\frac{\mathrm{d}^2Y}{\mathrm{d}X^2} + \frac{\mathrm{d}Y}{\mathrm{d}X} + \varepsilon^2 X Y = 0

despreciando ahora el último término, que es mucho más pequeño, nos quedamos con la ecuación diferencial

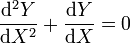
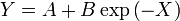
\frac{\mathrm{d}^2Y}{\mathrm{d}X^2} + \frac{\mathrm{d}Y}{\mathrm{d}X} = 0   \Rightarrow   Y = A + B \exp\left(-X\right)

Ahora sí podemos imponer la condición en x = 0 y escribir la solución interior como

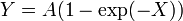
Y = A(1 - \exp(-X))\,

Pero ¿cuánto vale A?

5 El matching

Para poder hallar A debemos empalmar la solución interior con la exterior. Esto se hace imponiendo que sobre una escala intermedia entre x y X (mucho menor que x pero mucho mayor que X) ambas soluciones coincidan. En su versión más sencilla, se impone que el comportamiento, para x pequeño de la solución exterior coincida con el comportamiento, para X grande, de la solución interior, esto es,

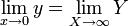
\lim_{x\to 0} y = \lim_{X\to\infty} Y

lo que nos da

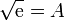
\sqrt{\mathrm{e}} = A\,

y por tanto la solución interior es

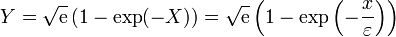
Y = \sqrt{\mathrm{e}}\left(1-\exp(-X)\right) = \sqrt{\mathrm{e}}\left(1-\exp\left(-\frac{x}{\varepsilon}\right)\right)

6 La solución uniforme

Tenemos entonces dos aproximaciones para la solución de la ecuación diferencial. Una que vale siempre que x no sea muy pequeño

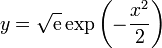
y = \sqrt{\mathrm{e}}\exp\left(-\frac{x^2}{2}\right)

y una que vale cuando x es muy pequeño (de orden \varepsilon o menor)

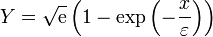
Y = \sqrt{\mathrm{e}}\left(1-\exp\left(-\frac{x}{\varepsilon}\right)\right)

¿Cómo podemos conseguir una solución aproximada para todo el intervalo? Recordemos el límite común de ambas funciones. Esto quiere decir que para x pequeño la solución exterior vale 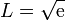L = \sqrt{\mathrm{e}} y para x finito la exterior vale lo mismo. Esto nos permite construir una solución uniforme sumando ambas y restando el límite común

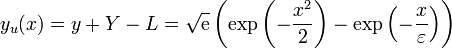
y_u(x) = y + Y - L = \sqrt{\mathrm{e}}\left(\exp\left(-\frac{x^2}{2}\right) - \exp\left(-\frac{x}{\varepsilon}\right)\right)

Esta es la solución que andábamos buscando. No cumple la ecuación diferencial en ningún punto, pero se diferencia de la solución en un término del orden de \varepsilon en todo el intervalo (de hecho, el error máximo es menor que el 1% en todo el intervalo.

7 Algunas gráficas

  • La solución calculada numéricamente
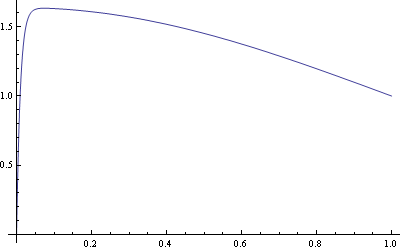
Imagen:gexacta.gif
  • Las soluciones interior y exterior
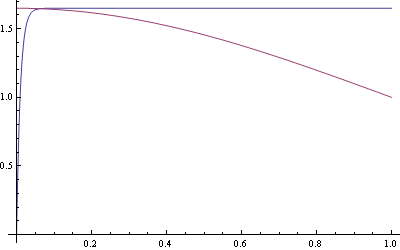
Imagen:gio.gif
  • La exacta y las dos aproximadas
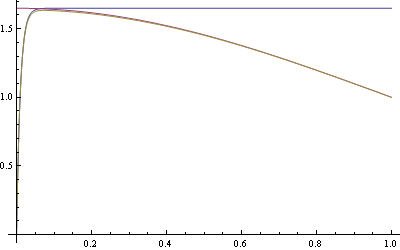
Imagen:geio.gif
  • La exacta y la solución uniforme
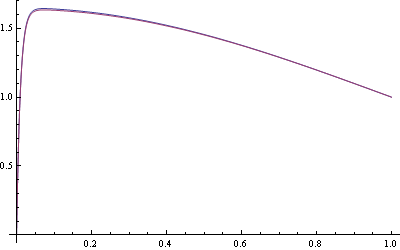
Imagen:geu.gif
  • Error absoluto en el intervalo
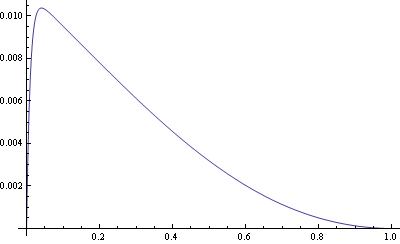
Imagen:eabs.gif
  • Error relativo en todo el intervalo
Imagen:erel.gif
Obtenido de "http://tesla.us.es/wiki/index.php/Problema_de_capa_l%C3%ADmite"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 13:02, 15 ago 2009. - Esta página ha sido visitada 1.555 veces. - Aviso legal - Acerca de Laplace