Una varilla y una carga
De Laplace
(→Flujo del campo eléctrico a través de superficie esférica) |
(→Flujo del campo eléctrico a través de superficie esférica) |
||
| Línea 19: | Línea 19: | ||
Sin embargo no es necesario realizar el cálculo explícito de la anterior integral ya que, en virtud de la '''Ley de Gauss''' se tiene que dicho flujo del campo eléctrico a través de una superficie cerrada es proporcional a la cantidiad de carga eléctrica encerrada en su interior. Dada las dimensiones y la posición de <math>\partial \tau</math> respecto del sistema de cargas, se tiene que sólo la mitad de la varilla se halla en el interior de dicha superficie esférica. Como la distribución de carga en la varilla es uniforme, habrá una cantidad de carga <math>\ Q/2</math> dentro de <math>\partial \tau</math>: | Sin embargo no es necesario realizar el cálculo explícito de la anterior integral ya que, en virtud de la '''Ley de Gauss''' se tiene que dicho flujo del campo eléctrico a través de una superficie cerrada es proporcional a la cantidiad de carga eléctrica encerrada en su interior. Dada las dimensiones y la posición de <math>\partial \tau</math> respecto del sistema de cargas, se tiene que sólo la mitad de la varilla se halla en el interior de dicha superficie esférica. Como la distribución de carga en la varilla es uniforme, habrá una cantidad de carga <math>\ Q/2</math> dentro de <math>\partial \tau</math>: | ||
| + | |||
| + | <center><math>\left.\begin{array}{l}\displaystyle \oint_{\partial \tau}\!\mathbf{E}\cdot \mathrm{d}\mathbf{S}=\frac{1}{\varepsilon_0} \, q\big|_\tau \\ \\ \displaystyle q\big|_\tau\int_C^D\!\lambda_e(z')\mathrm{d}l'=\frac{Q}{2a}\int_{-a/2}^{a/2}\!\mathrm{}z'=\frac{Q}{2}\end{array}\right\}</math>\quad {{tose}} \quad <math>\quad</math></center> | ||
[[Categoría:Problemas de electrostática en el vacío]] | [[Categoría:Problemas de electrostática en el vacío]] | ||
Revisión de 11:49 14 jul 2009
1 Enunciado
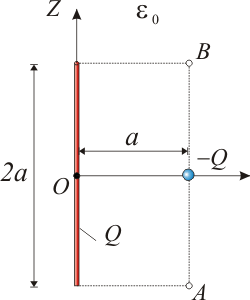
Una carga eléctrica Q está uniformemente distribuida a lo largo de un segmento rectilíneo de longitud 2a. A una distancia a del punto medio de dicho segmento y en dirección perpendicular a éste, se halla una carga puntual − Q.- Calcule el flujo del campo eléctrico a través de una superficie esférica de radio a / 2 centrada en el punto medio del segmento cargado (punto O).
- Obtenga la fuerza que actúa sobre la carga puntual.
- Calcule los momentos monopolar y dipolar de la distribución de carga descrita. Proponga expresiones aproximadas para el potencial y el campo eléctrico en puntos suficientemente alejados de la distribución.
- ¿Qué trabajo habría que realizar para mover la carga puntual entre los puntos A al B? (ver figura)
2 Solución
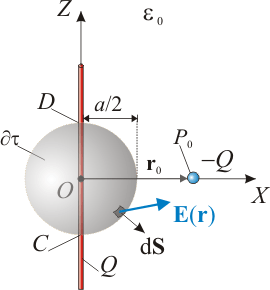
2.1 Flujo del campo eléctrico a través de superficie esférica
Tal como se indica en las figuras, adoptaremos un sistema de referencia cartesiano con origen en el centro de la varilla cargada, la cuál va a ser colineal con el eje 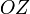 . Además, consideraremos que la carga puntual
. Además, consideraremos que la carga puntual 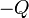 se halla en el eje
se halla en el eje 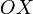 .
.
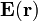 , a través de una superficie esférica
, a través de una superficie esférica 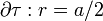 :
:

Nótese que dicho campo debe ser el creado por toda la distribución de carga descrita; es decir, la carga puntual 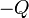 colocada en el punto dado por el vector
colocada en el punto dado por el vector 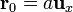 , y la varilla de longitud
, y la varilla de longitud 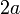 cargada uniformemente con una cantidad
cargada uniformemente con una cantidad  de carga eléctrica, o lo que es lo mismo, con una densidad lineal constante
de carga eléctrica, o lo que es lo mismo, con una densidad lineal constante 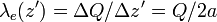 . La expresión del campo eléctrico de una carga puntual es bien conocida, y el cálculo del campo eléctrico creado por un segmento con densidad lineal de carga constante puede verse en el ejercicio Campo eléctrico de un segmento cargado.
. La expresión del campo eléctrico de una carga puntual es bien conocida, y el cálculo del campo eléctrico creado por un segmento con densidad lineal de carga constante puede verse en el ejercicio Campo eléctrico de un segmento cargado.
Sin embargo no es necesario realizar el cálculo explícito de la anterior integral ya que, en virtud de la Ley de Gauss se tiene que dicho flujo del campo eléctrico a través de una superficie cerrada es proporcional a la cantidiad de carga eléctrica encerrada en su interior. Dada las dimensiones y la posición de  respecto del sistema de cargas, se tiene que sólo la mitad de la varilla se halla en el interior de dicha superficie esférica. Como la distribución de carga en la varilla es uniforme, habrá una cantidad de carga
respecto del sistema de cargas, se tiene que sólo la mitad de la varilla se halla en el interior de dicha superficie esférica. Como la distribución de carga en la varilla es uniforme, habrá una cantidad de carga 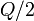 dentro de
dentro de  :
:
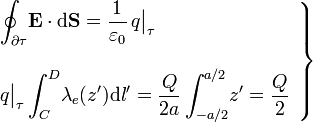 \quad
\quad  \quad
\quad