Masa que cuelga de dos muelles
De Laplace
(→Valores numéricos) |
(→Valores numéricos) |
||
| Línea 164: | Línea 164: | ||
[[Categoría:Problemas de movimiento oscilatorio]] | [[Categoría:Problemas de movimiento oscilatorio]] | ||
| + | [[Categoría:Problemas de examen]] | ||
Revisión de 10:38 8 jul 2009
Contenido |
1 Enunciado
Se tiene una masa m que cuelga de una asociación de dos muelles en paralelo con constantes recuperadoras k1 y k2 y longitudes naturales L1 y L2, respectivamente.
- Determine el valor de la elongación de la asociación en la situación de equilibrio.
- Se empuja la masa verticalmente hacia arriba con una velocidad inicial v0. Suponiendo que el rozamiento es despreciable, encuentre la evolución de la posición de la masa en el tiempo y el período de oscilación (Escoja como origen de coordenadas la posición de equilibrio del apartado anterior). Calcule la posición más alta que alcanza la masa y su energía en ese instante.
- Se añade un pistón de masa despreciable, de modo que se mueve dentro de un cilindro relleno con nitrógeno. Determine la longitud de onda de la onda de sonido generada en el cilindro, considerando que el gas es ideal.
- Determine los valores numÚricos de las magnitudes pedidas en los apartados anteriores.
Datos: 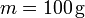 ,
, 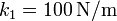 ,
, 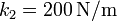 ,
,
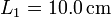 ,
, 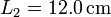 ,
, 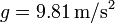 ,
, 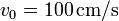 ,
, 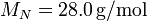 ,
, 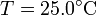
2 Elongación de equilibrio
La condición de equilibrio para la masa es
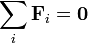
donde las fuerzas que actúan sobre la masa son las dos fuerzas elásticas y el peso. Tomando, como se indica, el eje Y vertical y hacia abajo, las fuerzas valen

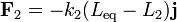

Sumando e igualando a cero, puesto que solo tenemos una componente,
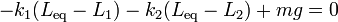
y despejando
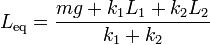
Vemos que la posición de equilibrio no es igual al peso dividida por la constante de la asociación, ya que hay que tener en cuenta la diferencia en las longitudes naturales.
3 Propiedades de la oscilación
3.1 Ecuación de movimiento
Consideremos ahora la dinámica de la masa. La segunda ley de Newton para el movimiento es
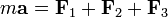
donde ahora ya las fuerzas no tienen los valores de la posición del equilibrio, sino que dependen de la posición de la masa.
Si describimos la posición de la masa por la coordenada y, medida desde la posición de equilibrio, tenemos que la elongación de cada muelle es
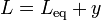
Teniendo en cuenta que el movimiento es unidimensional, la ecuación de movimiento queda
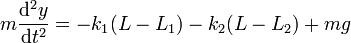
Sustituyendo y agrupando términos
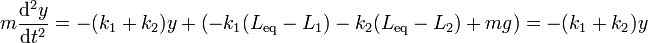
Esta es la ecuación de movimiento de un oscilador armónico
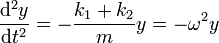
donde la frecuencia de oscilación y el periodo son
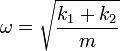

Vemos que la asociación de dos muelles en paralelo se comporta como uno solo de constante k1 + k2 a la hora de describir las oscilaciones en torno a la posición de equilibrio, no al punto de anclaje. O, dicho de otro modo, que la fórmula sencilla keq = k1 + k2 solo vale cuando la longitud natural es nula.
3.2 Ley horaria
La solución de esta ecuación diferencial es
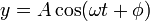
con A la amplitud de las oscilaciones y φ la constante de fase.
Determinamos A y φ de las condiciones iniciales. Sabemos que cuando se encuentra en la posición de equilibrio (y=0) se mueve con velocidad hacia arriba − v0 (ya que el eje apunta hacia abajo). Por tanto tenemos el sistema
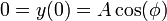
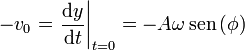
De la primera tenemos que
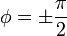
pero el signo del desfase no lo sabemos aún, pues tanto +90° como -90° tienen coseno nulo. El signo lo da la segunda ecuación. puesto que tanto v0 como la amplitud y la frecuencia son cantidades positivas, debe ser
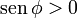

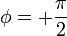
y
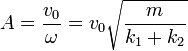
Por tanto, la ley horaria queda
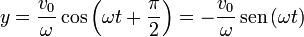
3.2.1 Forma alternativa
Otra forma de obtener la ley horaria es partir de la solución general, escrita como,
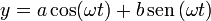
Imponiendo aquí las condiciones iniciales
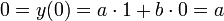
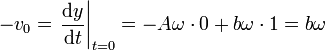
de donde
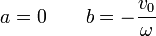

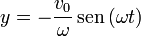
3.3 Máxima altura
La máxima altura se dará cuando el seno vale 1 (ya que y va hacia abajo), esto es, cuando
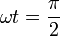

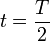

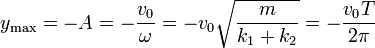
3.4 Energía en el máximo
En el punto de máxima altura la energía cinética es nula y toda la energía es potencial, con valor

Esta energía naturalmente coincide con la energía cinética inicial, pues al no haber rozamiento, la energía mecánica se conserva. Inicialmente es toda cinética y nada potencial (ya que ésta se mide respecto a la posición de equilibrio). En la elongación máxima es toda potencial y nada de cinética, pero su valor total es el mismo.
4 Onda sonora
El pistón conectado a la masa excita una onda sonora, que se propagará a la velocidad del sonido en el gas (que no es el aire). Si suponemos éste ideal, esta velocidad es
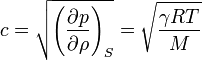
donde γ = cp / cV, el cociente entre las capacidades caloríficas a presión y volumen constante, que para el nitrógeno (gas diatómico) vale 7/5. R es la constante de los gases ideales, T es la temperatura absoluta del gas y M (o Pm) el peso molecular del gas.
La longitud de la onda que excita el pistón la da el que la frecuencia de vibración de esta onda es la misma que la de oscilación del pistón, que a la vez coincide con la de la masa sujeta a los muelles. Por tanto
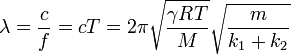
5 Valores numéricos
Sustituyendo los valores del enunciado obtenemos
- Posición de equilibrio
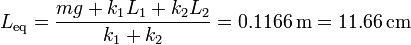
- Frecuencia angular de oscilación
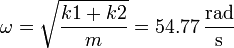
- Periodo de oscilación
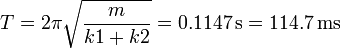
- Amplitud de oscilación
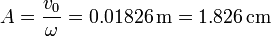
- Ley horaria
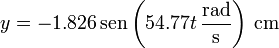
- Altura del máximo
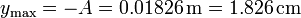
- Energía en el máximo
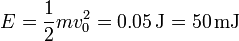
- Velocidad del sonido
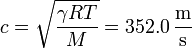
- Longitud de onda