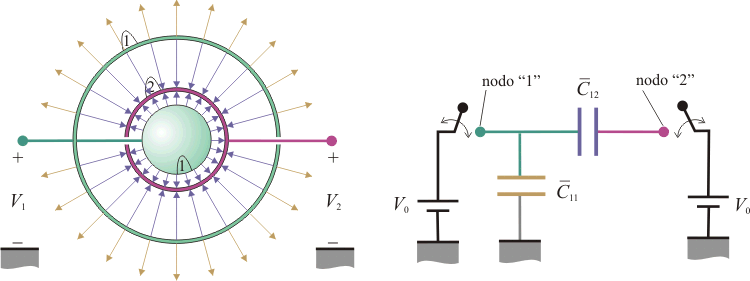
Tres superficies conductoras esféricas concéntricas
De Laplace
(→Circuito equivalente y matriz de coeficientes de capacidad) |
(→Circuito equivalente y matriz de coeficientes de capacidad) |
||
| Línea 14: | Línea 14: | ||
Consideremos ambos conductores “1” y “2” cargados y/o conectados a fuentes, de manera que el potencial electrostático tendrá un valor <math>V_2</math> en la superficie conductora intermedia de radio <math>a/2</math>, y un valor <math>V_1</math> en las superficies exterior e interior, de radios <math>a</math> y <math>a/3</math>, respectivamente. Si, en general, estos valores son no nulos y distintos, habrá líneas de campo eléctrico entre la superficie exterior de la esfera de mayor radio (conductor <math>1</math>) y el infinito. También habrá líneas de campo eléctrico en los espacios que hay entre las tres superficies conductoras, debido a la diferencia de potencial <math>\Delta V=V_1-V_2</math> que existe entre ellas. | Consideremos ambos conductores “1” y “2” cargados y/o conectados a fuentes, de manera que el potencial electrostático tendrá un valor <math>V_2</math> en la superficie conductora intermedia de radio <math>a/2</math>, y un valor <math>V_1</math> en las superficies exterior e interior, de radios <math>a</math> y <math>a/3</math>, respectivamente. Si, en general, estos valores son no nulos y distintos, habrá líneas de campo eléctrico entre la superficie exterior de la esfera de mayor radio (conductor <math>1</math>) y el infinito. También habrá líneas de campo eléctrico en los espacios que hay entre las tres superficies conductoras, debido a la diferencia de potencial <math>\Delta V=V_1-V_2</math> que existe entre ellas. | ||
| - | [[Imagen: | + | <center>[[Imagen:P1_i.gif|center]]</center> |
El circuito equivalente estará formado por dos nodos (uno por cada conductor) y tierra. Entre ésta y el nodo “1” habrá una autocapacidad <math>\overline{C}_{11}</math> que modela las líneas de campo entre la superficie esférica de mayor radio y el infinito. En consecuencia, <math>\overline{C}_{11}</math> debe ser la capacidad eléctrica de una superficie conductora esférica de radio <math>a</math>. Además, dicha superficie apantalla completamente a la intermedia, impidienddo la existencia de líneas de campo entre el conductor “2”, por lo que la autocapacidad entre el nodo “2” y tierra es siempre nula. Se tendrá, por tanto: | El circuito equivalente estará formado por dos nodos (uno por cada conductor) y tierra. Entre ésta y el nodo “1” habrá una autocapacidad <math>\overline{C}_{11}</math> que modela las líneas de campo entre la superficie esférica de mayor radio y el infinito. En consecuencia, <math>\overline{C}_{11}</math> debe ser la capacidad eléctrica de una superficie conductora esférica de radio <math>a</math>. Además, dicha superficie apantalla completamente a la intermedia, impidienddo la existencia de líneas de campo entre el conductor “2”, por lo que la autocapacidad entre el nodo “2” y tierra es siempre nula. Se tendrá, por tanto: | ||
Revisión de 12:16 4 jul 2009
Contenido |
1 Enunciado
El sistema de la figura está formado por tres superficies conductoras esféricas concéntricas de espesor despreciable y radios a, a / 2 y a / 3. Las superficies de mayor y menor radio están conectadas por un hilo conductor, formando el conductor “1”, que puede conectarse a una fuente de potencial V0. Dicho hilo pasa a través de un orificio practicado en la superficie de radio a / 2 (conductor “2”), sin tocarla. Otro hilo conductor permite conectar esta superficie intermedia con la fuente de potencial V0 a trav\'{e}s de otro orificio existente en al superficie esférica exterior. El espesor de los hilos y el tamaño de los orificios son despreciables frente al tamaño de las superficies.
- Obtenga un circuito equivalente para el sistema de conductores descrito y calcule su matriz de coeficientes de capacidad.
- Estando el conductor “1” descargado, se conecta el “2” a la fuente de potencial. Determine la carga eléctrica que se localiza en este conductor y el potencial a que se encuentra el “1”.
- Posteriormente, el conmutador del sistema conecta la fuente al conductor “1”, desconectándola del “2”. Calcule las cargas y los potenciales en los conductores para esta nueva situación. Especifique la cantidad de carga almacenada en cada una de las caras de las tres superficies esféricas.
- Determine la energía suministrada por la fuente en los procesos descritos en los apartados anteriores.
2 Solución
2.1 Circuito equivalente y matriz de coeficientes de capacidad
En primer lugar insistiremos en la idea de que, aunque el sistema descrito está formado por tres superficies conductoras, éstas se hayan conectadas de forma que sólo hay dos conductores “activos”; es decir, que se pueden conectar a una fuente para cargarlos o fijar su valor de potencial. Por otra parte, como en el enunciado no se indica explícitamente que algún conductor esté conectado a tierra, la referencia para la medida del potencial electrostático estará en el infinito. Consideremos ambos conductores “1” y “2” cargados y/o conectados a fuentes, de manera que el potencial electrostático tendrá un valor V2 en la superficie conductora intermedia de radio a / 2, y un valor V1 en las superficies exterior e interior, de radios a y a / 3, respectivamente. Si, en general, estos valores son no nulos y distintos, habrá líneas de campo eléctrico entre la superficie exterior de la esfera de mayor radio (conductor 1) y el infinito. También habrá líneas de campo eléctrico en los espacios que hay entre las tres superficies conductoras, debido a la diferencia de potencial ΔV = V1 − V2 que existe entre ellas.
El circuito equivalente estará formado por dos nodos (uno por cada conductor) y tierra. Entre ésta y el nodo “1” habrá una autocapacidad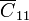 
que modela las líneas de campo entre la superficie esférica de mayor radio y el infinito. En consecuencia, 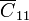debe ser la capacidad eléctrica de una superficie conductora esférica de radio a. Además, dicha superficie apantalla completamente a la intermedia, impidienddo la existencia de líneas de campo entre el conductor “2”, por lo que la autocapacidad entre el nodo “2” y tierra es siempre nula. Se tendrá, por tanto:
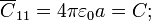
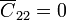
Obsérvese que los conductores “1” y “2” forman dos condensadores esféricos distintos: la cara exterior de la esfera de menor radio, y la interior de radio intermedio se hallan en influencia total
La capacidad eléctrica 
modela las líneas de campo entre los conductores “1” y “2”; es decir, entre la superficies exterior y la intermedia, y entre ésta y la interior. Tomando como origen el centro común de las tres superficies y utilizando las coordenadas esféricas, se tendrá que las superficies conductoras Σ:r = (a / 3) + y Σ:r = (a / 2) − , y las superficies Σ:r = (a / 2) + y Σ:r = a − , forman sendos condensadores esféricos, cuyas capacidades eléctricas son de la forma
siendo rint y rext respectivos radiosn interior y exterior del condesador.
