Derivada direccional
De Laplace
(→La derivada de una función de una variable) |
(→Interpretación geométrica de la derivada) |
||
| Línea 22: | Línea 22: | ||
===La derivada como operador=== | ===La derivada como operador=== | ||
| - | + | ||
===Extensión a tres dimensiones=== | ===Extensión a tres dimensiones=== | ||
Revisión de 18:54 10 dic 2007
Contenido |
1 Introducción
1.1 La derivada de una función de una variable
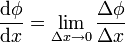
Gráficamente, antes de tomar el límite, el cociente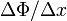 
representa la pendiente de una recta secante a la gráfica de la función, siendo uno de los puntos de corte aquél en que queremos calcular la derivada y el otro que vamos acercando progresivamente hacia el primer punto. Cuando tomamos el límite, ambos puntos coinciden y la secante se convierte en la tangente.
Podemos interpretar la expresión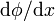 
de dos formas.
1.2 La derivada como cociente
La definición como límite de un cociente permite leer la expresión 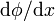como un cociente en sí mismo, entre:
- La cantidad
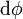, conocida como el diferencial de la función 
. Este diferencial se interpreta como un incremento infinitamente pequeño de la función entre dos puntos vecinos.
- La cantidad dx,, conocida como el diferencial de
, que representa la diferencia entre dos posiciones infinitamente próximas.
De esta interpretación como cociente se obtiene de forma inmediata que, por ejemplo, las dimensiones de la derivada 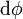son las de divididas por las de (verbigracia, que si el espacio se mide en metros y el tiempo en segundos, la velocidad -que es la derivada del espacio respecto al tiempo- se mide en metros/segundo).
1.3 La derivada como operador
1.4 Extensión a tres dimensiones
2 Definición
3 Derivadas parciales
4 Ejemplo
5 Enlaces
- Siguiente: Diferencial de una función
