Derivada direccional

De Laplace

Revisión de 19:59 5 dic 2007 (ver código fuente) Gonfer (Discusión | contribuciones) (→La derivada de una función de una variable) ← Edición más antigua		Revisión de 11:31 10 dic 2007 (ver código fuente) Gonfer (Discusión | contribuciones) (→La derivada de una función de una variable) Edición más nueva →
Línea 6:		Línea 6:
	<center><math>\frac{\mathrm{d}\phi}{\mathrm{d}x} = \lim_{\Delta x \to 0} \frac{\Delta \phi}{\Delta x}</math></center>		<center><math>\frac{\mathrm{d}\phi}{\mathrm{d}x} = \lim_{\Delta x \to 0} \frac{\Delta \phi}{\Delta x}</math></center>
-	Gráficamente, antes de tomar el límite, el cociente <math>\Delta\Phi/\Delta x\,</math> representa la pendiente de una recta secante a la gráfica de la función, siendo uno de los puntos de corte aquél en que queremos calcular la derivada y el otro que vamos acercando progresivamente hacia el primer punto. Cuando tomamos el límite, ambos puntos coinciden y la secante se convierte en la tangente.	+	[[Imagen:derivada.gif|right]]Gráficamente, antes de tomar el límite, el cociente <math>\Delta\Phi/\Delta x\,</math> representa la pendiente de una recta secante a la gráfica de la función, siendo uno de los puntos de corte aquél en que queremos calcular la derivada y el otro que vamos acercando progresivamente hacia el primer punto. Cuando tomamos el límite, ambos puntos coinciden y la secante se convierte en la tangente.
	===Interpretación geométrica de la derivada===		===Interpretación geométrica de la derivada===

---

Revisión de 11:31 10 dic 2007

Contenido 1 Introducción 1.1 La derivada de una función de una variable 1.2 Interpretación geométrica de la derivada 1.3 Extensión a tres dimensiones 2 Definición 3 Derivadas parciales 4 Ejemplo 5 Enlaces

1 Introducción

1.1 La derivada de una función de una variable

En una dimensión el concepto de derivada es relativamente sencillo: es el límite del cociente entre el incremento de una función y el incremento de su variable

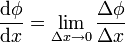
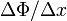Gráficamente, antes de tomar el límite, el cociente representa la pendiente de una recta secante a la gráfica de la función, siendo uno de los puntos de corte aquél en que queremos calcular la derivada y el otro que vamos acercando progresivamente hacia el primer punto. Cuando tomamos el límite, ambos puntos coinciden y la secante se convierte en la tangente.

1.2 Interpretación geométrica de la derivada

1.3 Extensión a tres dimensiones

2 Definición

3 Derivadas parciales

4 Ejemplo

5 Enlaces

• Siguiente: Diferencial de una función