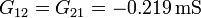Intersección de dos pistas

De Laplace

Revisión de 16:47 2 jun 2009 (ver código fuente) Antonio (Discusión | contribuciones) (→Corriente en el tercer electrodo) ← Edición más antigua		Revisión de 17:09 2 jun 2009 (ver código fuente) Antonio (Discusión | contribuciones) Edición más nueva →
Línea 23:		Línea 23:
	<center><math>I_3 = -(I_1 + I_2+I_0)\,</math></center>		<center><math>I_3 = -(I_1 + I_2+I_0)\,</math></center>
-	Pero, por la simetría I_0 = I_2 =	+	Pero, por la simetría,
		+
		+	<center><math>I_0 = I_2 = -2.63\,\mathrm{mA}</math></center>
		+
		+	y la corriente que entra por el electrodo 3 es
		+
		+	<center><math>I_3 = -I_1 - I_2-I_0 = -7.04\,\mathrm{mA}+2\times 2.63\,\mathrm{mA} = -1.78\,\mathrm{mA}</math></center>
		+
		+	Obsérvese que no hace falta diseñar ningún circuito previo, y que la única hipótesis es suponer que la corriente se distribuye por igual a la derecha y a la izquierda.
	==Coeficientes de conductancia==		==Coeficientes de conductancia==
		+	Si tenemos las corrientes que llegan a ciertos electrodos cuando uno de ellos se encuentra a un cierto voltaje y el resto a tierra podemos calcular los coeficientes de conductancia simplemente dividiendo. Si es V_1 la que está fijada y <math>V_2 = V_3 = 0\,\mathrm{mV}</math> será
		+
		+	<center><math>I_1 = G_{11}V_1+\overbrace{G_{12}V_2}^{=0}+\overbrace{G_{13}V_3}^{=0} = G_{11}V_1</math> {{tose}} <math>G_{11}=\frac{I_1}{V_1}=0.587\,\mathrm{mS}</math></center>
		+
		+	Del mismo modo se hallan <math>G_{21}</math> y <math>G_{31}</math>
		+
		+	<center><math>G_{21}=\frac{I_2}{V_1}=-0.219\,\mathrm{mS}</math>{{qquad}}{{qquad}}<math>G_{31}=\frac{I_3}{V_1}=-0.148\,\mathrm{mS}</math></center>
		+
		+	Ya tenemos la primera columna de la matriz de conductancias. La simetría de la matriz nos da los elementos restantes de la primera fila
		+	<center>
		+	<math>G_{12}=G_{21}=-0.219\,\mathrm{mS}</math>{{qquad}}{{qquad}}<math>G_{13}=G_{31}=-0.148\,\mathrm{mS}</math></center>
		+
		+
	==Circuito equivalente==		==Circuito equivalente==
	==Caso particular==		==Caso particular==
	==Potencia disipada==		==Potencia disipada==
	[[Categoría:Problemas de corriente eléctrica]]		[[Categoría:Problemas de corriente eléctrica]]

---

Revisión de 17:09 2 jun 2009

Contenido 1 Enunciado 2 Corriente en el tercer electrodo 3 Coeficientes de conductancia 4 Circuito equivalente 5 Caso particular 6 Potencia disipada

1 Enunciado

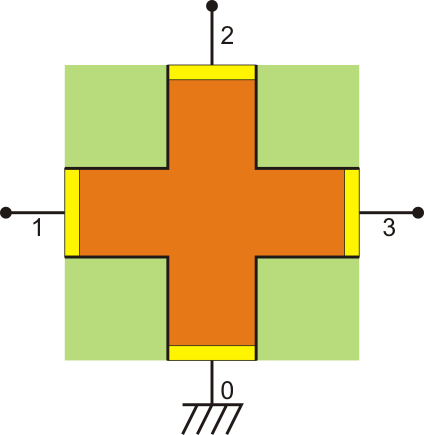
Una intersección de dos pistas en un circuito integrado se puede modelar como una cruz con brazos de igual longitud a la cual están conectados tres electrodos “vivos” (“1” a “3”) y uno de tierra (“0”), según se indica en la figura. Se sabe que cuando el electrodo 1 se encuentra a una tensión de +12 V y el resto a tierra, por el electrodo 1 entra una corriente de +7.04 mA, mientras que por el conductor 2 entra (según el criterio usual de signos) una de −2.63 mA.

1. Determine la corriente que entra (siguiendo el mismo criterio) por el electrodo 3 en la situación anterior.
2. Halle la matriz de coeficientes de conductancia del sistema de tres electrodos vivos.
3. Construya un circuito equivalente para el sistema de electrodos, que no emplee nodos intermedios. Halle los valores de las resistencias de este circuito.
4. Si el electrodo 1 se deja a +12 V y el 3 a tierra, pero el 2 se pone a −5 V. ¿Cuánta corriente entrará por cada electrodo vivo?
5. Para el caso original y para el del apartado anterior, ¿cuánta potencia se disipa en el sistema?

2 Corriente en el tercer electrodo

La clave de este problema es hacer uso de la simetría del sistema. Al tener forma de cruz griega (con los brazos iguales) vamos a poder tratar todos los electrodos de forma análoga.

En la situación descrita, la corriente entra por el electrodo 1 (lo que corresponde al signo positivo para la corriente), y a partir de ahí se distribuye y sale por los otros tres (que tendrán, por tanto, corrientes de entrada negativas). Sin embargo, no se distribuye entre los tres por igual. Si así fuera no necesitaríamos conocer la corriente por el electrodo 2.

La corriente se repartirá por igual a la izquierda y a la derecha, pero no necesariamente fluirá la misma corriente hacia el electrodo 3.

Podemos encontrar el valor de esta última corriente simplemente restando. En un estado estacionario

y de aquí

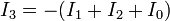
Pero, por la simetría,

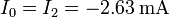
y la corriente que entra por el electrodo 3 es

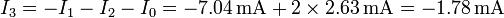
Obsérvese que no hace falta diseñar ningún circuito previo, y que la única hipótesis es suponer que la corriente se distribuye por igual a la derecha y a la izquierda.

3 Coeficientes de conductancia

Si tenemos las corrientes que llegan a ciertos electrodos cuando uno de ellos se encuentra a un cierto voltaje y el resto a tierra podemos calcular los coeficientes de conductancia simplemente dividiendo. Si es V_1 la que está fijada y 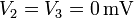será

      

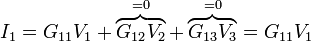
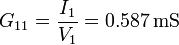
Del mismo modo se hallan G₂₁ y G₃₁

        

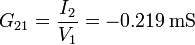
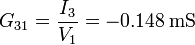
Ya tenemos la primera columna de la matriz de conductancias. La simetría de la matriz nos da los elementos restantes de la primera fila

        

4 Circuito equivalente

5 Caso particular

6 Potencia disipada