Ejemplos de superficies equiescalares
De Laplace
(→Un ejemplo aparentemente más complicado) |
|||
| Línea 1: | Línea 1: | ||
| - | == | + | ==Superficies de fase constante== |
| - | + | ||
| - | + | ||
| - | + | ||
Sea <math>\mathbf{A}\,</math> un vector constante y <math>\mathbf{r}\,</math> el vector de posición. Construimos un campo escalar <math>\phi\,</math> multiplicándolos escalarmente. Para describir las superficies equipotenciales podemos suponer que <math>\mathbf{A}\,</math> tiene componentes según los tres ejes de coordenadas, pero en realidad no tenemos por qué. | Sea <math>\mathbf{A}\,</math> un vector constante y <math>\mathbf{r}\,</math> el vector de posición. Construimos un campo escalar <math>\phi\,</math> multiplicándolos escalarmente. Para describir las superficies equipotenciales podemos suponer que <math>\mathbf{A}\,</math> tiene componentes según los tres ejes de coordenadas, pero en realidad no tenemos por qué. | ||
| Línea 20: | Línea 17: | ||
Estos planos son perpendiculares al eje <math>OZ\,</math>. Por tanto, las superficies equipotenciales del campo <math>\phi = \mathbf{A}\cdot\mathbf{r}\,</math> son planos paralelos entre sí y perpendiculares al vector <math>\mathbf{A}\,</math>. | Estos planos son perpendiculares al eje <math>OZ\,</math>. Por tanto, las superficies equipotenciales del campo <math>\phi = \mathbf{A}\cdot\mathbf{r}\,</math> son planos paralelos entre sí y perpendiculares al vector <math>\mathbf{A}\,</math>. | ||
| - | == | + | ==Un campo inversamente proporcional a la distancia== |
Aunque en cartesianas la visualización del campo <math>\phi = |\mathbf{r}|^2\,</math> es sencilla, en coordenadas esféricas es inmediata ya que <math> |\mathbf{r}| = r</math>, con r la coordenada esférica radial. Por tanto las superficies equiescalares cumplen | Aunque en cartesianas la visualización del campo <math>\phi = |\mathbf{r}|^2\,</math> es sencilla, en coordenadas esféricas es inmediata ya que <math> |\mathbf{r}| = r</math>, con r la coordenada esférica radial. Por tanto las superficies equiescalares cumplen | ||
| Línea 28: | Línea 25: | ||
esto es, son esferas con centro el origen (las [[Coordenadas esféricas. Líneas y superficies coordenadas|superficies coordenadas]] de la coordenada radial). | esto es, son esferas con centro el origen (las [[Coordenadas esféricas. Líneas y superficies coordenadas|superficies coordenadas]] de la coordenada radial). | ||
| - | == | + | ==Simetría traslacional== |
El campo <math>\phi = |\mathbf{r}|^2 + \mathbf{A}\cdot\mathbf{r}\,</math> es la suma de los dos anteriores. Sin embargo, sus superficies equiescalares no son la suma de nada, ya que no se pueden sumar planos con esferas. | El campo <math>\phi = |\mathbf{r}|^2 + \mathbf{A}\cdot\mathbf{r}\,</math> es la suma de los dos anteriores. Sin embargo, sus superficies equiescalares no son la suma de nada, ya que no se pueden sumar planos con esferas. | ||
| Línea 48: | Línea 45: | ||
<center><math>\mathbf{C} = -\frac{A}{2}\mathbf{u}_z = - \frac{\mathbf{A}}{2} \qquad R(k) = \sqrt{k + \frac{A^2}{2}}</math></center> | <center><math>\mathbf{C} = -\frac{A}{2}\mathbf{u}_z = - \frac{\mathbf{A}}{2} \qquad R(k) = \sqrt{k + \frac{A^2}{2}}</math></center> | ||
| - | ===Un ejemplo aparentemente más complicado | + | ==Simetría acimutal== |
| + | |||
| + | ==Un ejemplo aparentemente más complicado== | ||
Supongamos que se nos pide dibujar las superficies equiescalares del campo | Supongamos que se nos pide dibujar las superficies equiescalares del campo | ||
Revisión de 19:11 1 dic 2007
Contenido |
1 Superficies de fase constante
Sea 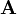 un vector constante y
un vector constante y 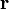 el vector de posición. Construimos un campo escalar
el vector de posición. Construimos un campo escalar  multiplicándolos escalarmente. Para describir las superficies equipotenciales podemos suponer que
multiplicándolos escalarmente. Para describir las superficies equipotenciales podemos suponer que 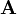 tiene componentes según los tres ejes de coordenadas, pero en realidad no tenemos por qué.
tiene componentes según los tres ejes de coordenadas, pero en realidad no tenemos por qué.
Puesto que los ejes no están fijados de antemano, podemos elegirlos como más nos convenga. En particular, podemos tomar el eje  apuntando en la dirección de
apuntando en la dirección de 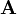 , de forma que este vector se escribe
, de forma que este vector se escribe
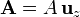
y el campo escalar  es simplemente
es simplemente
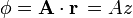
por tanto las superficies equiescalares son planos paralelos
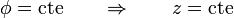
Estos planos son perpendiculares al eje  . Por tanto, las superficies equipotenciales del campo
. Por tanto, las superficies equipotenciales del campo 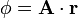 son planos paralelos entre sí y perpendiculares al vector
son planos paralelos entre sí y perpendiculares al vector 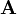 .
.
2 Un campo inversamente proporcional a la distancia
Aunque en cartesianas la visualización del campo 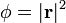 es sencilla, en coordenadas esféricas es inmediata ya que
es sencilla, en coordenadas esféricas es inmediata ya que 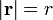 , con r la coordenada esférica radial. Por tanto las superficies equiescalares cumplen
, con r la coordenada esférica radial. Por tanto las superficies equiescalares cumplen
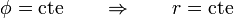
esto es, son esferas con centro el origen (las superficies coordenadas de la coordenada radial).
3 Simetría traslacional
El campo  es la suma de los dos anteriores. Sin embargo, sus superficies equiescalares no son la suma de nada, ya que no se pueden sumar planos con esferas.
es la suma de los dos anteriores. Sin embargo, sus superficies equiescalares no son la suma de nada, ya que no se pueden sumar planos con esferas.
Si, como en el ejemplo anterior, tomamos el eje  como el que apunta en la dirección de
como el que apunta en la dirección de 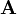 , podemos escribir el campo en cartesianas como
, podemos escribir el campo en cartesianas como

y las superficies equiescalares cumplen
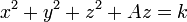
Sumando el mismo término en ambos miembros queda
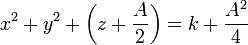
que son las ecuaciones de esferas concéntricas, con centro y radio
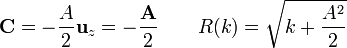
4 Simetría acimutal
5 Un ejemplo aparentemente más complicado
Supongamos que se nos pide dibujar las superficies equiescalares del campo
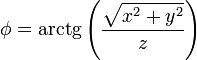
Aunque de entrada puede parecer complicado, si recordamos las relaciones entre los distintos sistemas de coordenadas podemos ver que
y por tanto las superficies 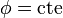 son conos rectos con vértice el origen y eje el eje
son conos rectos con vértice el origen y eje el eje  .
.





