Inmersión de un bloque metálico en agua
De Laplace
(Diferencias entre revisiones)
(→Temperatura final) |
|||
| Línea 15: | Línea 15: | ||
Sustituyendo | Sustituyendo | ||
| - | <center><math>(50000\,\mathrm{g})\left(0.095\,\frac{\mathrm{cal}}{\mathrm{g}\cdot^\circ\mathrm{C}}(60^\circ\mathrm{C}-t) = 120000\,\mathrm{g}\left(0.095\,\frac{\mathrm{cal}}{\mathrm{g}\cdot^\circ\mathrm{C}}(t-25^\circ\mathrm{C})</math></center> | + | <center><math>(50000\,\mathrm{g})\left(0.095\,\frac{\mathrm{cal}}{\mathrm{g}\cdot^\circ\mathrm{C}}\right)(60^\circ\mathrm{C}-t) = 120000\,\mathrm{g}\left(0.095\,\frac{\mathrm{cal}}{\mathrm{g}\cdot^\circ\mathrm{C}}\right)(t-25^\circ\mathrm{C})</math></center> |
que tiene por solución | que tiene por solución | ||
<center><math>t = 26.3^\circ\mathrm{C}\,</math></center> | <center><math>t = 26.3^\circ\mathrm{C}\,</math></center> | ||
| + | |||
==Variación de la entropía== | ==Variación de la entropía== | ||
[[Categoría:Problemas del segundo principio de la termodinámica]] | [[Categoría:Problemas del segundo principio de la termodinámica]] | ||
Revisión de 13:42 30 abr 2009
Contenido |
1 Enunciado
Un bloque de cobre de 50 kg a 80°C se deja caer en un tanque aislado adiabáticamente que contiene 120 l de agua a 25°C. Determine la temperatura final de equilibrio y la variación total del entropía.
Dato: cp(cobre) = 0.095 cal/g·°C.
2 Temperatura final
Al sumergirse, el cobre se enfría, cediendo calor al agua, que se calienta. El equilibrio se alcanza cuando ambos se ponen la misma temperatura.
La temperatura de equilibrio la obtenemos igualando el calor cedido por el cobre con el absorbido por el agua
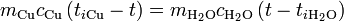
Sustituyendo

que tiene por solución