Rendimiento de aparatos hipotéticos
De Laplace
(→Motor hipotético) |
(→Refrigerador hipotético) |
||
| Línea 18: | Línea 18: | ||
Para el caso de los refrigeradores, en lugar del rendimiento se usa el ''coeficiente de desempeño'' (COP, por las siglas de “''coefficient of performance''”), que se define usando el mismo principio que para el rendimiento: | Para el caso de los refrigeradores, en lugar del rendimiento se usa el ''coeficiente de desempeño'' (COP, por las siglas de “''coefficient of performance''”), que se define usando el mismo principio que para el rendimiento: | ||
| - | <center><math>COP = \frac{\mbox{lo que se | + | <center><math>\mathrm{COP} = \frac{\mbox{lo que se obtiene}}{\mbox{lo que cuesta}}</math></center> |
| + | donde en este caso “lo que se obtiene” es la extracción de un calor <math>|Q_f|</math> del foco frío y “lo que cuesta” es el trabajo necesario para hacer funcionar el refrigerador: | ||
| + | |||
| + | <center><math>\mathrm{COP} = \frac{|Q_f|}{|W|}</math></center> | ||
| + | |||
| + | A diferencia del rendimiento, el COP sí puede ser mayor que la unidad. Puesto que, por el primer principio el trabajo realizado por el sistema es la diferencia entre el calor que entra y el calor que sale, podemos expresar el COP en función del calor solamente | ||
| + | |||
| + | <center><math>\mathrm{COP} = \frac{|Q_f|}{|Q_c|-|Q_f|} = \frac{1}{\displaystyle\frac{|Q_c|}{|Q_f|}-1}</math></center> | ||
| + | |||
| + | Como con el rendimiento de las máquinas térmicas, existe un límite al coeficiente de desempeño de un refrigerador. Este límite lo da un ''refrigerador de Carnot'', que es una máquina de Carnot a la que, por ser reversible, se ha hecho funcionar en sentido inverso. El COP de un refrigerador de Carnot es | ||
| + | |||
| + | <center><math>\mathrm{COP}_\mathrm{max} =\frac{1}{\displaystyle\frac{|Q_c|}{|Q_f|}-1} = \frac{1}{T_c/T_f-1}</math></center> | ||
| + | |||
| + | Para los datos del enunciado | ||
[[Categoría:Problemas del segundo principio de la termodinámica]] | [[Categoría:Problemas del segundo principio de la termodinámica]] | ||
Revisión de 19:03 29 abr 2009
1 Enunciado
Un inventor mantiene que ha desarrollado una máquina térmica que recibe 700 kJ de calor desde un foco térmico a 500 K y produce 300 kJ de trabajo neto transfiriendo el calor sobrante a un foco térmico a 290 K. ¿Es razonable?
Nuestro inventor vuelve a la carga, esta vez con un refrigerador que, asegura, mantiene el espacio refrigerado a 2°C mientras el ambiente se encuentra a 24°C, teniendo una eficiencia de 13.5. ¿Le hacemos caso?
2 Motor hipotético
El rendimiento de la supuesta máquina inventada es

El rendimiento máximo posible es el de una máquina de Carnot que trabaje entre las dos temperaturas indicadas. Este es
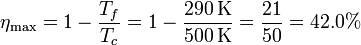
Puesto que el rendimiento alegado es superior al máximo posible, concluimos que la invención es fraudulenta.
3 Refrigerador hipotético
Para el caso de los refrigeradores, en lugar del rendimiento se usa el coeficiente de desempeño (COP, por las siglas de “coefficient of performance”), que se define usando el mismo principio que para el rendimiento:
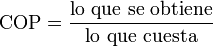
donde en este caso “lo que se obtiene” es la extracción de un calor | Qf | del foco frío y “lo que cuesta” es el trabajo necesario para hacer funcionar el refrigerador:
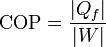
A diferencia del rendimiento, el COP sí puede ser mayor que la unidad. Puesto que, por el primer principio el trabajo realizado por el sistema es la diferencia entre el calor que entra y el calor que sale, podemos expresar el COP en función del calor solamente
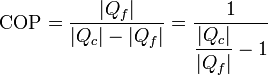
Como con el rendimiento de las máquinas térmicas, existe un límite al coeficiente de desempeño de un refrigerador. Este límite lo da un refrigerador de Carnot, que es una máquina de Carnot a la que, por ser reversible, se ha hecho funcionar en sentido inverso. El COP de un refrigerador de Carnot es
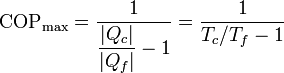
Para los datos del enunciado





