Ciclo Otto
De Laplace
(→Eficiencia en función del calor) |
(→Trabajo realizado) |
||
| Línea 54: | Línea 54: | ||
como se comprueba sustituyendo las relaciones anteriores. | como se comprueba sustituyendo las relaciones anteriores. | ||
| + | |||
| + | ==Rendimiento== | ||
| + | El rendimiento de una máquina térmica se define, en general como “lo que sacamos dividido por lo que nos cuesta”. En este caso, lo que sacamos es el trabajo neto útil, <math>|W|</math>. Lo que nos cuesta es el calor <math>Q_c</math>, que introducimos en la combustión. No podemos restarle el calor <math>|Q_f|</math> ya que ese calor se cede al ambiente y no es reutilizado (lo que violaría el [[enunciado de Kelvin-Planck]]). Por tanto | ||
| + | |||
| + | <center><math>\eta = \frac{|W|}{|Q_c|}</math></center> | ||
| + | |||
| + | Sustituyendo el trabajo como diferencia de calores | ||
| + | |||
| + | <center><math>\eta = \frac{|Q_c|-|Q_f|}{|Q_c|}=1-\frac{|Q_f|}{|Q_c|}</math></center> | ||
| + | |||
| + | Esta es la expresión general del rendimiento de una máquina térmica. | ||
==Eficiencia en función de las temperaturas== | ==Eficiencia en función de las temperaturas== | ||
Revisión de 12:25 24 abr 2009
Contenido |
1 Enunciado
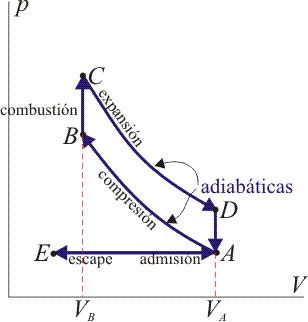
Un ciclo Otto ideal modela el comportamiento de un motor de explosión. Este ciclo está formado por seis pasos, según seindica en la figura. Pruebe que el rendimiento de este ciclo viene dado por la expresión
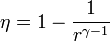
siendo r = V2 / V1 la razón de compresión. Para ello, halle el rendimiento a partir del calor que entra en el sistema y el que sale de él; exprese el resultado en términos de las temperaturas en los vértices del ciclo y, con ayuda de la ley de Poisson, relacione este resultado con los volúmenes V1 y V2.
2 Descripción del ciclo
Un ciclo Otto ideal es una aproximación teórica al comportamiento de un motor de explosión. Las fases de operación de este motor son las siguientes:- Admisión (1)
- El pistón baja con la válvula de admisión abierta, aumentando la cantidad de mezcla (aire + combustible) en la cámara. Esto se modela como una expansión a presión constante (ya que al estar la válvula abierta la presión es igual a la exterior). En el diagrama PV aparece como la línea recta E→A.
- Compresión (2)
- El pistón sube comprimiendo la mezcla. Dada la velocidad del proceso se supone que la mezcla no tiene posibilidad de intercambiar calor con el ambiente, por lo que el proceso es adiabático. Se modela como la curva adiabática reversible A→B, aunque en realidad no lo es por la presencia de factores irreversibles como la fricción.
- Explosión
- Con el pistón en su punto más alto, salta la chispa de la bujía. El calor generado en la combustión calienta bruscamente el aire, que incrementa su temperatura a volumen prácticamente constante (ya que al pistón no le ha dado tiempo a bajar). Esto se representa por una isócora B→C. Este paso es claramente irreversible, pero para el caso de un proceso isócoro en un gas ideal el balance es el mismo que en uno reversible.
- Expansión (3)
- La alta temperatura del gas empuja al pistón hacia abajo, realizando trabajo sobre él. De nuevo, por ser un proceso muy rápido se aproxima por una curva adiabática reversible C→D.
- Escape (4)
- Se abre la válvula de escape y el gas sale al exterior, empujado por el pistón a una temperatura mayor que la inicial, siendo sustituido por la misma cantidad de mezcla fría en la siguiente admisión. El sistema es realmente abierto, pues intercambia masa con el exterior. No obstante, dado que la cantidad de aire que sale y la que entra es la misma podemos, para el balance energético, suponer que es el mismo aire, que se ha enfriado. Este enfriamiento ocurre en dos fases. Cuando el pistón está en su punto más bajo, el volumen permanece aproximadamente constante y tenemos la isócora D→A. Cuando el pistón empuja el aire hacia el exterior, con la válvula abierta, empleamos la isobara A→E, cerrando el ciclo.
En total, el ciclo se compone de dos subidas y dos bajadas del pistón, razón por la que se le llama motor de cuatro tiempos.
3 Eficiencia en función del calor
Al analizar el ciclo Otto ideal, podemos despreciar en el balance los procesos de admisión y de escape a presión constante A→E y E→A, ya que al ser idénticos y reversibles, en sentido opuesto, todo el calor y el trabajo que se intercambien en uno de ellos, se cancela con un término opuesto en el otro.
3.1 Intercambio de calor
De los cuatro procesos que forman el ciclo cerrado, no se intercambia calor en los procesos adiabáticos A→B y C→D, por definición. Sí se intercambia en los dos procesos isócoros.
- En la ignición de la mezcla B→C, una cierta cantidad de calor Qc (procedente de la energía interna del combustible) se transfiere al aire. Dado que el proceso sucede a volumen constante, el calor coincide con el aumento de la energía interna
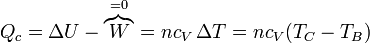
- En la expulsión de los gases D→A el aire sale a una temperatura mayor que a la entrada, liberando posteriormente un calor | Qf | al ambiente. En el modelo de sistema cerrado, en el que nos imaginamos que es el mismo aire el que se comprime una y otra vez en el motor, modelamos esto como que el calor | Qf | es liberado en el proceso D→A, por enfriamiento. El valor absoluto viene de que, siendo un calor que sale del sistema al ambiente, su signo es negativo. Su valor, análogamente al caso anterior, es
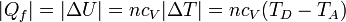
3.2 Trabajo realizado
De forma opuesta a lo que ocurre con el calor, no se realiza trabajo sobre el sistema en los dos procesos isócoros. Sí se realiza en los dos adiabáticos.
- En la compresión de la mezcla A→B, se realiza un trabajo positivo sobre el gas. Al ser un proceso adiabático, todo este trabajo se invierte en incrementar la energía interna, elevando su temperatura:
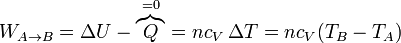
- En la expansión C→D es el aire el que realiza trabajo sobre el pistón. De nuevo este trabajo útil equivale a la variación de la energía interna
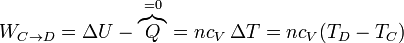
- este trabajo es negativo, por ser el sistema el que lo realiza.
- El trabajo útil realizado por el motor será el trabajo neto entregado, igual a lo que produce (en valor absoluto) menos lo que emplea en funcionar
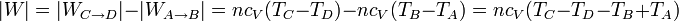
Por tratarse de un proceso cíclico, la variación de la energía interna es nula al finalizar el ciclo. Esto implica que el calor neto introducido en el sistema debe ser igual al trabajo neto realizado por este, en valor absoluto.
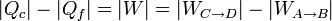
como se comprueba sustituyendo las relaciones anteriores.
4 Rendimiento
El rendimiento de una máquina térmica se define, en general como “lo que sacamos dividido por lo que nos cuesta”. En este caso, lo que sacamos es el trabajo neto útil, | W | . Lo que nos cuesta es el calor Qc, que introducimos en la combustión. No podemos restarle el calor | Qf | ya que ese calor se cede al ambiente y no es reutilizado (lo que violaría el enunciado de Kelvin-Planck). Por tanto
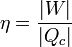
Sustituyendo el trabajo como diferencia de calores
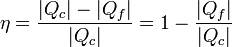
Esta es la expresión general del rendimiento de una máquina térmica.