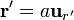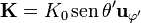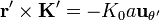Campo magnético de una esfera rotatoria
De Laplace
(→Momento dipolar) |
(→Densidad de corriente) |
||
| Línea 19: | Línea 19: | ||
y un movimiento de rotación, empleando coordenadas esféricas | y un movimiento de rotación, empleando coordenadas esféricas | ||
| - | <center><math>\mathbf{v}=\mathbf{w}\times\mathbf{r}=(\omega \mathbf{u}_z)\times(a\mathbf{u} | + | <center><math>\mathbf{v}=\mathbf{w}\times\mathbf{r}=(\omega \mathbf{u}_z)\times(a\mathbf{u}_{r'})=\omega a\,\mathrm{sen}\,\theta'\,\mathbf{u}_{\varphi'}</math></center> |
y esto nos da la densidad de corriente | y esto nos da la densidad de corriente | ||
| - | <center><math>\mathbf{K}=\frac{Q\omega}{4\pi a}\,\mathrm{sen}\,\theta\,\mathbf{u}_\varphi=K_0\,\mathrm{sen}\,\theta\,\mathbf{u}_\varphi</math></center> | + | <center><math>\mathbf{K}=\frac{Q\omega}{4\pi a}\,\mathrm{sen}\,\theta'\,\mathbf{u}_{\varphi'}=K_0\,\mathrm{sen}\,\theta'\,\mathbf{u}_{\varphi'}</math></center> |
==Campo en el eje== | ==Campo en el eje== | ||
Revisión de 17:37 18 abr 2009
Contenido |
1 Enunciado
Una esfera de radio a almacena una carga Q distribuida uniformemente en su superficie. La esfera gira con velocidad angular ω alrededor de un eje.
-
 Determine la densidad de corriente en la esfera
Determine la densidad de corriente en la esfera
-
 Calcule, por integración directa, el campo magnético en los puntos del eje de rotación.
Calcule, por integración directa, el campo magnético en los puntos del eje de rotación.
-
 Calcule el momento dipolar magnético de la esfera. A partir de aquí, halle el campo en puntos alejados de la esfera, no necesariamente en el eje.
Calcule el momento dipolar magnético de la esfera. A partir de aquí, halle el campo en puntos alejados de la esfera, no necesariamente en el eje.
-
 Halle, resolviendo las ecuaciones de la magnetostática, el campo en todos los puntos del espacio.
Halle, resolviendo las ecuaciones de la magnetostática, el campo en todos los puntos del espacio.
2 Densidad de corriente
Puesto que la densidad de carga se encuentra sobre la superficie de la esfera, la densidad de corriente resultante va a ser una superficial, 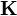 . Si tenemos una distribución de carga superficial fijada en un sólido, el cual se mueve con velocidad
. Si tenemos una distribución de carga superficial fijada en un sólido, el cual se mueve con velocidad  , la densidad de corriente será
, la densidad de corriente será
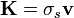
puesto que todos los portadores de carga de un elemento de superficie se mueven con la misma velocidad.
Para el caso de distribución uniforme
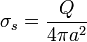
y un movimiento de rotación, empleando coordenadas esféricas
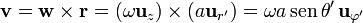
y esto nos da la densidad de corriente
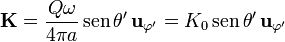
3 Campo en el eje
4 Momento dipolar
El momento dipolar magnético para una distribución de corriente superficial es
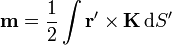
Empleando coordenadas esféricas, cada uno de los términos de esta integral valen