Ecuación de estado
De Laplace
(Nueva página: == Enunciado == Utilizando la ecuación de estado de los gases ideales, responda a las siguientes preguntas #¿Que volumen ocupa un mol de gas en condiciones estándar? #¿Cuantas mo...) |
(→Solución) |
||
| Línea 7: | Línea 7: | ||
== Solución == | == Solución == | ||
| + | |||
| + | === Volumen de un mol de gas en condiciones estándar === | ||
| + | |||
| + | Las condiciones estándar son una presión de 1 atm y una temperatura de <math>0^o</math> C. A partir de la ecuación de | ||
| + | estado de los gases ideales obtenemos | ||
| + | <center> | ||
| + | <math> | ||
| + | \displaystyle V = \frac{nRT}{P}=\frac{1\times8.31\times273.15}{1}\mathrm{\frac{mol\,J\,K}{mol\,K\,atm}} | ||
| + | \mathrm{\frac{1\,atm}{101325\,Pa}}=22.4\,\mathrm{l} | ||
| + | </math> | ||
| + | </center> | ||
| + | Hay que recordar siempre que la temperatura de la ecuación de estado del gas ideal es absoluta, es decir, hay | ||
| + | que expresarl en Kelvin. | ||
| + | |||
| + | También es habitual encontrar la referencia a '''condiciones normales'''. Esto quiere decir una presión de 1 atm y una temperatura de 25<math>^o</math> C. En el caso de condiciones normales el volumen ocupado por un mol de gas ideal | ||
| + | es | ||
| + | <center> | ||
| + | <math> | ||
| + | \displaystyle V = \frac{nRT}{P}=\frac{1\times8.31\times298.15}{1}\mathrm{\frac{mol\,J\,K}{mol\,K\,atm}} | ||
| + | \mathrm{\frac{1\,atm}{101325\,Pa}}=24.5\,\mathrm{l} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | === Numero de moléculas === | ||
| + | |||
| + | Podemos calcular el número de moles en las condiciones dadas por el enunciado. Usando la ecuación de estado | ||
| + | obtenemos | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \displaystyle n=\frac{PV}{RT}=\frac{1\times 1}{0.082\times300}\mathrm{\frac{atm\,cm^3\,mol\,K}{atm\,l\,K}} | ||
| + | \mathrm{\frac{1\,l}{10^3cm^3}}=4.07\times10^{-5}\,\mathrm{mol} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | En 1 mol hay <math>N_A</math> moléculas, Entonces el número de moléculas total es | ||
| + | <center> | ||
| + | <math> | ||
| + | N=nN_A=2.45\times10^{19}\,\mathrm{molec.} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | Para hacerse una idea de lo grande que es este número, imaginemos que contamos las moléculas de modo que empleamos | ||
| + | 1 ms en contabilizar cada una de ellas. El tiempo total que emplearíamos sería | ||
| + | <center> | ||
| + | <math> | ||
| + | T=10^{-3}N=2.45\times10^{16}\,\mathrm{seg}=7.77\times10^{8}\,\mathrm{a\tilde{n}os} | ||
| + | </math> | ||
| + | </center> | ||
| + | La edad estimada del Universo es de 15000 millones de años, es decir <math>1.5\times10^{10}</math>años | ||
| + | |||
| + | Si la presión es de sólo <math>10^{-8}</math> torr el número de moléculas es menor. Expresando la presión en | ||
| + | atmósferas tenemos | ||
| + | <center> | ||
| + | <math> | ||
| + | P=10^{-8}\,\mathrm{torr\frac{1\,atm}{760\,torr}}=1.32\times10^{-11}\,\mathrm{atm} | ||
| + | </math> | ||
| + | </center> | ||
| + | El número de moléculas sería | ||
| + | <center> | ||
| + | <math> | ||
| + | N = N_A\frac{PV}{RT}=3.23\times10^8\,\mathrm{molec.} | ||
| + | </math> | ||
| + | </center> | ||
| + | Sigue siendo un número muy grande, aunque la presión sea muy baja. Si las contamos con el procedimiento anterior | ||
| + | tardaríamos un tiempo | ||
| + | <center> | ||
| + | <math> | ||
| + | T=10^{-3}N=3.23\times10^5\,\mathrm{seg}=3.74\,\mathrm{dias} | ||
| + | </math> | ||
| + | </center> | ||
Revisión de 13:49 16 abr 2009
Contenido |
1 Enunciado
Utilizando la ecuación de estado de los gases ideales, responda a las siguientes preguntas
- ¿Que volumen ocupa un mol de gas en condiciones estándar?
- ¿Cuantas moléculas hay en
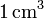de gas ideal a una temperatura de 300 K y a una presión de 1 atm?
¿Y si la presión es de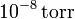 
?
2 Solución
2.1 Volumen de un mol de gas en condiciones estándar
Las condiciones estándar son una presión de 1 atm y una temperatura de 0o C. A partir de la ecuación de estado de los gases ideales obtenemos
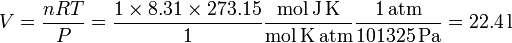
Hay que recordar siempre que la temperatura de la ecuación de estado del gas ideal es absoluta, es decir, hay que expresarl en Kelvin.
También es habitual encontrar la referencia a condiciones normales. Esto quiere decir una presión de 1 atm y una temperatura de 25o C. En el caso de condiciones normales el volumen ocupado por un mol de gas ideal es
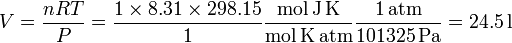
2.2 Numero de moléculas
Podemos calcular el número de moles en las condiciones dadas por el enunciado. Usando la ecuación de estado obtenemos
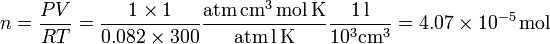
En 1 mol hay NA moléculas, Entonces el número de moléculas total es
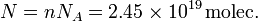
Para hacerse una idea de lo grande que es este número, imaginemos que contamos las moléculas de modo que empleamos 1 ms en contabilizar cada una de ellas. El tiempo total que emplearíamos sería
La edad estimada del Universo es de 15000 millones de años, es decir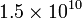 
años
Si la presión es de sólo 10 − 8 torr el número de moléculas es menor. Expresando la presión en atmósferas tenemos
El número de moléculas sería
Sigue siendo un número muy grande, aunque la presión sea muy baja. Si las contamos con el procedimiento anterior tardaríamos un tiempo
