Fuerza magnética sobre un dipolo eléctrico
De Laplace
(→Fuerza) |
(→Enunciado) |
||
| (10 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| - | |||
==Enunciado== | ==Enunciado== | ||
| - | Un dipolo eléctrico, que puede suponerse formado por dos cargas puntuales <math>\pm q</math> situadas en los extremos de una varilla corta, de longitud <math>L = p/q</math>, se mueve en el interior de un campo magnético. El movimiento del dipolo puede describirse mediante la velocidad de su centro, <math>\mathbf{v}</math>, y la velocidad angular con la que gira en torno a él, <math>\mathbf{w}</math>. | + | {{nivel|4}} Un dipolo eléctrico, que puede suponerse formado por dos cargas puntuales <math>\pm q</math> situadas en los extremos de una varilla corta, de longitud <math>L = p/q</math>, se mueve en el interior de un campo magnético. El movimiento del dipolo puede describirse mediante la velocidad de su centro, <math>\mathbf{v}</math>, y la velocidad angular con la que gira en torno a él, <math>\mathbf{w}</math>. |
# Calcule la fuerza que el campo magnético ejerce sobre el dipolo. | # Calcule la fuerza que el campo magnético ejerce sobre el dipolo. | ||
| Línea 9: | Línea 8: | ||
La velocidad de los puntos de un sólido tiene la forma general | La velocidad de los puntos de un sólido tiene la forma general | ||
| - | <center><math>\mathbf{v}=\mathbf{v} | + | <center><math>\mathbf{v}=\mathbf{v}_O+\mathbf{w}\times(\mathbf{r}-\mathbf{r}_O)\,</math></center> |
| - | siendo <math>\mathbf{v} | + | siendo <math>\mathbf{v}_O</math> la velocidad de un punto, <math>\mathbf{w}</math> la velocidad angular con la que el sólido gira en torno a dicho punto y <math>\mathbf{r}-\mathbf{r}_O</math> la posición relativa respecto a ese centro. |
| + | |||
| + | Si consideramos que las dos cargas está situadas simétricamente respecto del centro del dipolo, sus posiciones son | ||
| + | |||
| + | <center><math>\mathbf{r}_+=\mathbf{r}_p + \frac{\Delta \mathbf{r}}{2}</math>{{qquad}}{{qquad}}<math>\mathbf{r}_-=\mathbf{r}_p - \frac{\Delta \mathbf{r}}{2}</math></center> | ||
| + | |||
| + | y sus velocidades | ||
| + | <center> | ||
| + | <math>\mathbf{v}_+=\mathbf{v}_p + \mathbf{w}\times\frac{\Delta \mathbf{r}}{2}</math>{{qquad}}{{qquad}}<math>\mathbf{v}_-=\mathbf{v}_p - \mathbf{w}\times\frac{\Delta \mathbf{r}}{2}</math> | ||
| + | </center> | ||
| + | |||
| + | La fuerza sobre el dipolo será la suma de la [[fuerza de Lorentz]] sobre cada carga | ||
| + | |||
| + | <center><math>\mathbf{F}=q\mathbf{v}_+\times\mathbf{B}(\mathbf{r}_+)+(-q)\mathbf{v}_-\times\mathbf{B}(\mathbf{r}_-)</math></center> | ||
| + | |||
| + | Sustituyendo las posiciones y la velocidades quedan dos términos | ||
| + | |||
| + | <center><math>\mathbf{F}=\mathbf{F}_1+\mathbf{F}_2</math></center> | ||
| + | |||
| + | El primero es debido a la velocidad de traslación | ||
| + | |||
| + | <center><math>\mathbf{F}=q\mathbf{v}_p\times\left(\mathbf{B}(\mathbf{r}_p + {\Delta \mathbf{r}}/{2})-\mathbf{B}(\mathbf{r}_p - {\Delta \mathbf{r}}/{2})\right) \simeq q\Delta\mathbf{r}\cdot\nabla(\mathbf{v}_p\times\mathbf{B})=(\mathbf{p}\cdot\nabla)(\mathbf{v}\times\mathbf{B})</math></center> | ||
| + | |||
| + | donde hemos usado que la diferencia entre los valores de una función evaluada en dos puntos próximos es el diferencial de la función. | ||
| + | |||
| + | El segundo término es el debido a la rotación | ||
| + | |||
| + | <center> | ||
| + | <math>\mathbf{F}_2=q\left(\mathbf{w}\times\frac{\Delta\mathbf{r}}{2}\right)\times\mathbf{B}+(-q)\left(-\mathbf{w}\times\frac{\Delta\mathbf{r}}{2}\right)\times\mathbf{B}=(\mathbf{w}\times\mathbf{p})\times\mathbf{B}</math></center> | ||
| + | |||
| + | Reuniendo los dos términos | ||
| + | |||
| + | <center><math>\mathbf{F}=(\mathbf{p}\cdot\nabla)(\mathbf{v}\times\mathbf{B})+(\mathbf{w}\times\mathbf{p})\times\mathbf{B}</math></center> | ||
| + | |||
| + | donde, por abreviar, podemos ya usar <math>\mathbf{v}</math> para la velocidad del dipolo puntual. En el caso de un campo uniforme el primer término, que contiene una derivada, se anula y la fuerza se reduce a | ||
| + | |||
| + | <center><math>\mathbf{F}=(\mathbf{w}\times\mathbf{p})\times\mathbf{B}\,</math></center> | ||
| + | |||
| + | Esto quiere decir que, en un campo magnético uniforme, la fuerza sobre un dipolo eléctrico no depende de la velocidad con la que se traslada, sino de la velocidad con que gira sobre sí mismo. | ||
==Momento== | ==Momento== | ||
| + | El cálculo del momento de las fuerzas aplicadas es similar al de la fuerza | ||
| + | |||
| + | <center><math>\mathbf{M}=\mathbf{r}_+\times\mathbf{F}_++\mathbf{r}_-\times\mathbf{F}_-</math></center> | ||
| + | |||
| + | Sustituyendo las dos posiciones | ||
| + | |||
| + | <center><math>\mathbf{F}=\mathbf{r}_p\times(\mathbf{F}_++\mathbf{F}_-)+\frac{\Delta \mathbf{r}}{2}\times(\mathbf{F}_+-\mathbf{F}_-)</math></center> | ||
| + | |||
| + | El primer término es simplemente | ||
| + | |||
| + | <center><math>\mathbf{M}_1=\mathbf{r}_p\times\mathbf{F}\,</math></center> | ||
| + | |||
| + | En el segundo, teniendo en cuenta que <math>\Delta\mathbf{r}</math> es una cantidad pequeña | ||
| + | |||
| + | <center><math>\mathbf{M}_2=\frac{\Delta\mathbf{r}}{2}\times(q\mathbf{v}_p\times\mathbf{B}(\mathbf{r}_p))=\mathbf{p}\times(\mathbf{v}_p\times\mathbf{B})</math></center> | ||
| + | |||
| + | Aquí se ha despreciado los términos asociados a la rotación, puesto que son cuadráticos en <math>\Delta\mathbf{r}</math>. Esto nos da la expresión para el momento (omitiendo ya el subíndice <math>p</math>) | ||
| + | |||
| + | <center><math>\mathbf{M}=\mathbf{r}\times\mathbf{F}+\mathbf{p}\times(\mathbf{v}\times\mathbf{B})</math></center> | ||
| + | |||
| + | El segundo término representa el par intrínseco, que tiende hacer girar el dipolo sobre sí mismo. | ||
| + | |||
| + | <center><math>\mathbf{\tau}= \mathbf{p}\times(\mathbf{v}\times\mathbf{B})</math></center> | ||
| + | |||
| + | Combinando los dos efectos tenemos que, en un campo uniforme: | ||
| + | |||
| + | * La fuerza, que produce traslación, depende de la velocidad con la que gira el dipolo. | ||
| + | |||
| + | * El par, que produce rotación, depende de la velocidad con que se traslada. | ||
| + | Este acoplamiento entre traslación y rotación puede producir comportamientos muy complicados e interesantes, para nada reducibles a órbitas circulares sencillas, como ocurre con las cargas aisladas. | ||
[[Categoría:Problemas de campo magnético de corrientes estacionarias]] | [[Categoría:Problemas de campo magnético de corrientes estacionarias]] | ||
última version al 16:51 29 mar 2009
1 Enunciado
![]() Un dipolo eléctrico, que puede suponerse formado por dos cargas puntuales
Un dipolo eléctrico, que puede suponerse formado por dos cargas puntuales 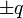 situadas en los extremos de una varilla corta, de longitud L = p / q, se mueve en el interior de un campo magnético. El movimiento del dipolo puede describirse mediante la velocidad de su centro,
situadas en los extremos de una varilla corta, de longitud L = p / q, se mueve en el interior de un campo magnético. El movimiento del dipolo puede describirse mediante la velocidad de su centro,  , y la velocidad angular con la que gira en torno a él,
, y la velocidad angular con la que gira en torno a él,  .
.
- Calcule la fuerza que el campo magnético ejerce sobre el dipolo.
- Halle el momento de la fuerza producido por el campo.
2 Fuerza
La velocidad de los puntos de un sólido tiene la forma general
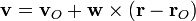
siendo  la velocidad de un punto,
la velocidad de un punto,  la velocidad angular con la que el sólido gira en torno a dicho punto y
la velocidad angular con la que el sólido gira en torno a dicho punto y  la posición relativa respecto a ese centro.
la posición relativa respecto a ese centro.
Si consideramos que las dos cargas está situadas simétricamente respecto del centro del dipolo, sus posiciones son


y sus velocidades


La fuerza sobre el dipolo será la suma de la fuerza de Lorentz sobre cada carga

Sustituyendo las posiciones y la velocidades quedan dos términos

El primero es debido a la velocidad de traslación
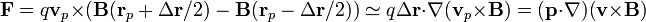
donde hemos usado que la diferencia entre los valores de una función evaluada en dos puntos próximos es el diferencial de la función.
El segundo término es el debido a la rotación

Reuniendo los dos términos

donde, por abreviar, podemos ya usar  para la velocidad del dipolo puntual. En el caso de un campo uniforme el primer término, que contiene una derivada, se anula y la fuerza se reduce a
para la velocidad del dipolo puntual. En el caso de un campo uniforme el primer término, que contiene una derivada, se anula y la fuerza se reduce a

Esto quiere decir que, en un campo magnético uniforme, la fuerza sobre un dipolo eléctrico no depende de la velocidad con la que se traslada, sino de la velocidad con que gira sobre sí mismo.
3 Momento
El cálculo del momento de las fuerzas aplicadas es similar al de la fuerza

Sustituyendo las dos posiciones

El primer término es simplemente

En el segundo, teniendo en cuenta que  es una cantidad pequeña
es una cantidad pequeña

Aquí se ha despreciado los términos asociados a la rotación, puesto que son cuadráticos en  . Esto nos da la expresión para el momento (omitiendo ya el subíndice p)
. Esto nos da la expresión para el momento (omitiendo ya el subíndice p)
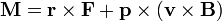
El segundo término representa el par intrínseco, que tiende hacer girar el dipolo sobre sí mismo.

Combinando los dos efectos tenemos que, en un campo uniforme:
- La fuerza, que produce traslación, depende de la velocidad con la que gira el dipolo.
- El par, que produce rotación, depende de la velocidad con que se traslada.
Este acoplamiento entre traslación y rotación puede producir comportamientos muy complicados e interesantes, para nada reducibles a órbitas circulares sencillas, como ocurre con las cargas aisladas.





