Fuerza magnética sobre un dipolo eléctrico
De Laplace
(→Fuerza) |
|||
| Línea 30: | Línea 30: | ||
<center><math>\mathbf{F}=\mathbf{F}_1+\mathbf{F}_2</math></center> | <center><math>\mathbf{F}=\mathbf{F}_1+\mathbf{F}_2</math></center> | ||
| - | El primero es debido a la velocidad de traslación | + | El primero es debido a la velocidad de traslación |
| - | <math>\mathbf{F}=q\mathbf{v}_p\times\left(\mathbf{B}(\mathbf{r}_p + {\Delta \mathbf{r}}/{2})-\mathbf{B}(\mathbf{r}_p - {\Delta \mathbf{r}}/{2})\right) \simeq q\Delta\mathbf{r}\cdot\nabla(\mathbf{v}_p\times\mathbf{B})=(\mathbf{p}\cdot\nabla)(\mathbf{v}\times\mathbf{B})</math></center> | + | <center><math>\mathbf{F}=q\mathbf{v}_p\times\left(\mathbf{B}(\mathbf{r}_p + {\Delta \mathbf{r}}/{2})-\mathbf{B}(\mathbf{r}_p - {\Delta \mathbf{r}}/{2})\right) \simeq q\Delta\mathbf{r}\cdot\nabla(\mathbf{v}_p\times\mathbf{B})=(\mathbf{p}\cdot\nabla)(\mathbf{v}\times\mathbf{B})</math></center> |
donde hemos usado que la diferencia entre los valores de una función evaluada en dos puntos próximos es el diferencial de la función. | donde hemos usado que la diferencia entre los valores de una función evaluada en dos puntos próximos es el diferencial de la función. | ||
| + | |||
| + | El segundo término es el debido a la rotación | ||
| + | |||
| + | <center> | ||
| + | <math>\mathbf{F}_2=q\left(\mathbf{w}\times\frac{\Delta\mathbf{r}}{2}\right)\times\mathbf{B}+(-q)\left(-\mathbf{w}\times\frac{\Delta\mathbf{r}}{2}\right)\times\mathbf{B}=(\mathbf{w}\times\mathbf{p})\times\mathbf{B}</math></center> | ||
| + | |||
| + | Reuniendo los dos términos | ||
| + | |||
| + | <center><math>\mathbf{F}=(\mathbf{p}\cdot\nabla)(\mathbf{v}\times\mathbf{B})+(\mathbf{w}\times\mathbf{p})\times\mathbf{B}</math></center> | ||
| + | |||
| + | donde, por abreviar, podemos ya usar <math>\mathbf{v}</math> para la velocidad del dipolo puntual. En el caso de un campo uniforme el primer término, que contiene una derivada, se anula y la fuerza se reduce a | ||
| + | |||
| + | <center><math>\mathbf{F}=(\mathbf{w}\times\mathbf{p})\times\mathbf{B}\,</math></center> | ||
| + | |||
| + | Esto quiere decir que, en un campo magnético uniforme, la fuerza sobre un dipolo eléctrico no depende de la velocidad con la que se traslada, sino de la velocidad con que gira sobre sí mismo. | ||
==Momento== | ==Momento== | ||
[[Categoría:Problemas de campo magnético de corrientes estacionarias]] | [[Categoría:Problemas de campo magnético de corrientes estacionarias]] | ||
Revisión de 15:52 29 mar 2009
1 Enunciado
Un dipolo eléctrico, que puede suponerse formado por dos cargas puntuales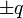 
situadas en los extremos de una varilla corta, de longitud L = p / q, se mueve en el interior de un campo magnético. El movimiento del dipolo puede describirse mediante la velocidad de su centro, 
, y la velocidad angular con la que gira en torno a él, 
.
- Calcule la fuerza que el campo magnético ejerce sobre el dipolo.
- Halle el momento de la fuerza producido por el campo.
2 Fuerza
La velocidad de los puntos de un sólido tiene la forma general
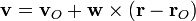
siendo 
la velocidad de un punto, la velocidad angular con la que el sólido gira en torno a dicho punto y 
la posición relativa respecto a ese centro.
Si consideramos que las dos cargas está situadas simétricamente respecto del centro del dipolo, sus posiciones son
y sus velocidades
La fuerza sobre el dipolo será la suma de la fuerza de Lorentz sobre cada carga
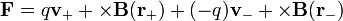
Sustituyendo las posiciones y la velocidades quedan dos términos
El primero es debido a la velocidad de traslación
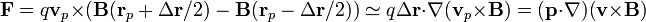
donde hemos usado que la diferencia entre los valores de una función evaluada en dos puntos próximos es el diferencial de la función.
El segundo término es el debido a la rotación
Reuniendo los dos términos
donde, por abreviar, podemos ya usar para la velocidad del dipolo puntual. En el caso de un campo uniforme el primer término, que contiene una derivada, se anula y la fuerza se reduce a
Esto quiere decir que, en un campo magnético uniforme, la fuerza sobre un dipolo eléctrico no depende de la velocidad con la que se traslada, sino de la velocidad con que gira sobre sí mismo.
