Entrar Página Discusión Historial Go to the site toolbox

Momento magnético de una esfera en rotación

De Laplace

(Diferencias entre revisiones)
(→Momento magnético)
(→Momento magnético)
Línea 6: Línea 6:
==Solución==
==Solución==
===Momento magnético===
===Momento magnético===
 +
====Antes de hacer ninguna cuenta====
 +
====Cálculo del momento====
El [[dipolo magnético|momento dipolar magnético]] de una distribución de corriente de volumen se calcula mediante la integral vectorial
El [[dipolo magnético|momento dipolar magnético]] de una distribución de corriente de volumen se calcula mediante la integral vectorial
Línea 67: Línea 69:
<center><math>\mathbf{m}=\frac{4\pi\rho_0wR^5}{15}\mathbf{u}_z=\frac{qR^2}{5}\mathbf{w}</math></center>
<center><math>\mathbf{m}=\frac{4\pi\rho_0wR^5}{15}\mathbf{u}_z=\frac{qR^2}{5}\mathbf{w}</math></center>
 +
====Interpretación====
El resultado final ya no depende de la elección de ejes. Simplemente, el momento dipolar apunta en la dirección del eje de giro.
El resultado final ya no depende de la elección de ejes. Simplemente, el momento dipolar apunta en la dirección del eje de giro.

Revisión de 13:51 28 mar 2009

Contenido

1 Enunciado

Calcule el momento magnético dipolar de una esfera de radio R, con una carga q distribuida uniformemente en su volumen y que gira con velocidad angular \mathbf{w}.

Establezca la proporcionalidad entre este momento magnético y el momento angular de la esfera, si ésta posee una masa m distribuida uniformemente en el volumen.

2 Solución

2.1 Momento magnético

2.1.1 Antes de hacer ninguna cuenta

2.1.2 Cálculo del momento

El momento dipolar magnético de una distribución de corriente de volumen se calcula mediante la integral vectorial

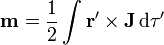
\mathbf{m}=\frac{1}{2}\int \mathbf{r}'\times\mathbf{J}\,\mathrm{d}\tau'

siendo el volumen de integración aquél en que hay corriente. En nuestro caso, se trata de la esfera de radio R. Por ello usaremos coordenadas esféricas para realizar el cálculo.

La densidad de corriente en el caso de que tengamos una distribución de carga que se mueve rígidamente es

\mathbf{J}=\rho_0 \mathbf{v}\,        \rho_0=\frac{q}{4\pi R^3/3}

La velocidad de los puntos de la esfera corresponde a una rotación pura

\mathbf{v}=\mathbf{w}\times\mathbf{r}'

Si tomamos como eje Z el marcado por la velocidad angular nos queda la densidad de corriente

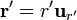
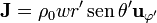
\mathbf{w}=w\mathbf{u}_z\,        \mathbf{r}'=r'\mathbf{u}_{r'}\,        \mathbf{J}=\rho_0wr'\,\mathrm{sen}\,\theta'\mathbf{u}_{\varphi'}

El último producto vectorial puede obtenerse usando las relaciones entre las bases vectoriales o la propia definición de producto vectorial como un vector cuyo módulo es el producto de los módulos por el seno del ángulo que forman (que es θ, por definición de esta coordenada), y con una dirección ortogonal a ambos.

Llevando esto a la integral nos queda el integrando

\mathbf{r}'\times\mathbf{J}=-\rho_0wr'^2\,\mathrm{sen}\,\theta'\,\mathbf{u}_{\theta'}

y nos queda el momento magnético

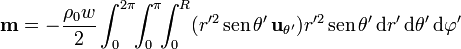
\mathbf{m}=-\frac{\rho_0w}{2}\int_0^{2\pi}\!\!\int_0^\pi\!\!\int_0^R (r'^2\,\mathrm{sen}\,\theta'\,\mathbf{u}_{\theta'})r'^2\,\mathrm{sen}\,\theta'\,\mathrm{d}r'\,\mathrm{d}\theta'\,\mathrm{d}\varphi'

Esta es una integral vectorial, por lo que hay que tener mucho cuidado con la base vdectorial empleada, ya que

Los vectores de la base dependen de la posición

Por ello, pasamos este vector a la base cartesiana

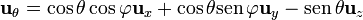
\mathbf{u}_{\theta}=\cos\theta\cos\varphi\mathbf{u}_{x}+\cos\theta\mathrm{sen}\,\varphi\mathbf{u}_{y}-\mathrm{sen}\,\theta\mathbf{u}_{z}

y la integral se puede descomponer en esta base

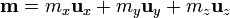
\mathbf{m}=m_x\mathbf{u}_x+m_y\mathbf{u}_y+m_z\mathbf{u}_z

con

m_x=-\frac{\rho_0w}{2}\int_0^{2\pi}\!\!\int_0^\pi\!\!\int_0^R r'^4\,\mathrm{sen}^2\theta'\cos\theta'\,\cos\varphi'\,\mathrm{d}r'\,\mathrm{d}\theta'\,\mathrm{d}\varphi'
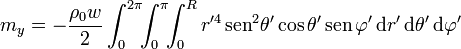
m_y=-\frac{\rho_0w}{2}\int_0^{2\pi}\!\!\int_0^\pi\!\!\int_0^R r'^4\,\mathrm{sen}^2\theta'\cos\theta'\,\mathrm{sen}\,\varphi'\,\mathrm{d}r'\,\mathrm{d}\theta'\,\mathrm{d}\varphi'
m_z=\frac{\rho_0w}{2}\int_0^{2\pi}\!\!\int_0^\pi\!\!\int_0^R r'^4\,\mathrm{sen}^3\theta'\,\mathrm{d}r'\,\mathrm{d}\theta'\,\mathrm{d}\varphi'

las dos primeras integrales se anulan ya que

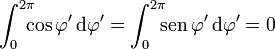
\int_0^{2\pi}\!\!\!\!\cos\varphi'\,\mathrm{d}\varphi'=\int_0^{2\pi}\!\!\!\mathrm{sen}\,\varphi'\,\mathrm{d}\varphi'=0

La tercera componente se convierte en un producto de tres integrales independientes

m_z=\frac{\rho_0w}{2}\int_0^{2\pi}\!\!\!\!\mathrm{d}\varphi'\int_0^\pi\!\!\mathrm{sen}^3\theta'\,\,\mathrm{d}\theta'\int_0^R r'^4\,\,\mathrm{d}r'=\frac{\rho_0w}{2}(2\pi)\left(\frac{4}{3}\right)\left(\frac{R^5}{5}\right)

Simplificando nos queda el momento dipolar magnético

\mathbf{m}=\frac{4\pi\rho_0wR^5}{15}\mathbf{u}_z=\frac{qR^2}{5}\mathbf{w}

2.1.3 Interpretación

El resultado final ya no depende de la elección de ejes. Simplemente, el momento dipolar apunta en la dirección del eje de giro.

Comprobemos que las dimensiones son correctas.

[m]=(1\,\mathrm{C})\left(1\,\mathrm{m}\right)^2\left(\frac{1}{\mathrm{s}}\right) = 1\mathrm{A}\cdot\mathrm{m}^2

2.2 Momento angular

2.3 Razón giromagnética

Obtenido de "http://tesla.us.es/wiki/index.php/Momento_magn%C3%A9tico_de_una_esfera_en_rotaci%C3%B3n"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace