Dipolo magnético
De Laplace
(→Desarrollo multipolar magnético) |
(→Desarrollo multipolar magnético) |
||
| Línea 16: | Línea 16: | ||
resulta (de forma no trivial) la expresión aproximada para el potencial vector | resulta (de forma no trivial) la expresión aproximada para el potencial vector | ||
| - | <center><math>\mathbf{A}=\frac{\mu_0\mathbf{m}\times\mathbf{r}}{r^3}</math></center> | + | <center><math>\mathbf{A}=\frac{\mu_0}{4\pi}\frac{\mathbf{m}\times\mathbf{r}}{r^3}</math></center> |
donde | donde | ||
Revisión de 13:47 26 mar 2009
Contenido |
1 Desarrollo multipolar magnético
Supongamos que tenemos una distribución de corriente estacionaria que ocupa una pequeña región del espacio y queremos hallar el campo en puntos alejados.
Cuando se dice “una pequeña región del espacio” se entiende que comparada con la distancia al punto de observación. Matemáticamente:
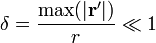
Como con el campo eléctrico, la idea del desarrollo multipolar es hacer un cálculo aproximado, más sencillo que la integral exacta (la cual puede ser imposible de calcular) mediante el empleo de una serie de Taylor. Partimos de la expresión del potencial vector para el caso de una espira
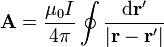
Aplicando el desarrollo del binomio de Newton
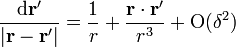
resulta (de forma no trivial) la expresión aproximada para el potencial vector
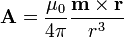
donde

es el momento magnético dipolar de la espira.
1.1 Demostración detallada
La obtención de la expresión aproximada del potencial vector no es elemental. Si sustituimos





