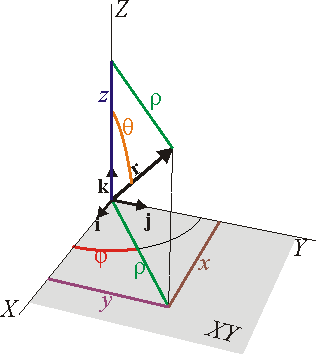
Relación entre los distintos sistemas de coordenadas
De Laplace
(Diferencias entre revisiones)
(→Entre cilíndricas y esféricas) |
(→Enlaces) |
||
| (11 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
==Entre cartesianas y cilíndricas== | ==Entre cartesianas y cilíndricas== | ||
| - | Con un poco de trigonometría se puede establecer la relación entre los tres sistemas. Entre cartesianas y esféricas tenemos que la coordenada <math>z,</math> es la misma, | + | [[Imagen:cil-esf.png|frame|right]]Con un poco de trigonometría se puede establecer la relación entre los tres sistemas. Entre cartesianas y esféricas tenemos que la coordenada <math>z,</math> es la misma, |
<center><math>z = z\,</math></center> | <center><math>z = z\,</math></center> | ||
| Línea 24: | Línea 24: | ||
Combinando las relaciones anteriores obtenemos el paso de esféricas a cartesianas. | Combinando las relaciones anteriores obtenemos el paso de esféricas a cartesianas. | ||
| - | <math>x = r\mathrm{sen}\,\theta\cos\varphi\qquad y = r\mathrm{sen}\,\theta\mathrm{sen}\,\varphi\qquad z = r\cos\theta</math> | + | <center><math>x = r\mathrm{sen}\,\theta\cos\varphi\qquad y = r\mathrm{sen}\,\theta\mathrm{sen}\,\varphi\qquad z = r\cos\theta</math></center> |
y sus correspondientes relaciones inversas | y sus correspondientes relaciones inversas | ||
| - | <math>r = \sqrt{x^2+y^2+z^2}\qquad \theta = \mathrm{arctg}\left(\frac{\sqrt{x^2+y^2}}{z}\right)\qquad \varphi = \mathrm{arctg}\left(\frac{y}{x}\right)</math> | + | <center><math>r = \sqrt{x^2+y^2+z^2}\qquad \theta = \mathrm{arctg}\left(\frac{\sqrt{x^2+y^2}}{z}\right)\qquad \varphi = \mathrm{arctg}\left(\frac{y}{x}\right)</math></center> |
| - | + | ||
==Algunos ejemplos numéricos== | ==Algunos ejemplos numéricos== | ||
| Línea 35: | Línea 35: | ||
Supongamos que debemos dar las coordenadas cilíndricas y esféricas del punto dado, en cartesianas, por | Supongamos que debemos dar las coordenadas cilíndricas y esféricas del punto dado, en cartesianas, por | ||
| - | <math>x=2\,\mathrm{m}\qquad y=-3\,\mathrm{m}\qquad z=4\,\mathrm{m}</math> | + | <center><math>x=2\,\mathrm{m}\qquad y=-3\,\mathrm{m}\qquad z=4\,\mathrm{m}</math></center> |
La misma posición, en cilíndricas, se expresa | La misma posición, en cilíndricas, se expresa | ||
| - | <math>\rho=\sqrt{x^2+y^2}=3.606\,\mathrm{m}\qquad {\varphi} = \mathrm{arctg}\left(-\frac{3}{2}\right)=-0.983\,\mathrm{rad}\qquad | + | <center><math>\rho=\sqrt{x^2+y^2}=3.606\,\mathrm{m}\qquad {\varphi} = \mathrm{arctg}\left(-\frac{3}{2}\right)=-0.983\,\mathrm{rad}\qquad |
| - | z=4\,\mathrm{m}</math> | + | z=4\,\mathrm{m}</math></center> |
y, en esféricas, | y, en esféricas, | ||
| - | <math>r=\sqrt{\rho^2+z^2}=5.385\,\mathrm{m}\qquad \theta=\mathrm{arctg}\left(\frac{3.606}{4}\right)=0.734\,\mathrm{rad}\qquad {\varphi}= -0.983\,\mathrm{rad}</math> | + | <center><math>r=\sqrt{\rho^2+z^2}=5.385\,\mathrm{m}\qquad \theta=\mathrm{arctg}\left(\frac{3.606}{4}\right)=0.734\,\mathrm{rad}\qquad {\varphi}= -0.983\,\mathrm{rad}</math></center> |
===De esféricas a otros sistemas=== | ===De esféricas a otros sistemas=== | ||
Ahora supongamos que nos dan un punto, en esféricas, de coordenadas | Ahora supongamos que nos dan un punto, en esféricas, de coordenadas | ||
| - | <math>r=3\,\mathrm{m}\qquad \theta=\frac{\pi}{6}\,\mathrm{rad}\qquad{\varphi}=\frac{\pi}{4}\,\mathrm{rad}</math> | + | <center><math>r=3\,\mathrm{m}\qquad \theta=\frac{\pi}{6}\,\mathrm{rad}\qquad{\varphi}=\frac{\pi}{4}\,\mathrm{rad}</math></center> |
Este mismo punto, en cilíndricas, es | Este mismo punto, en cilíndricas, es | ||
| - | <math>\rho=1.5\,\mathrm{m}\qquad {\varphi}=\frac{\pi}{4}\,\mathrm{rad}\qquad z =2.598\,\mathrm{m}</math> | + | <center><math>\rho=1.5\,\mathrm{m}\qquad {\varphi}=\frac{\pi}{4}\,\mathrm{rad}\qquad z =2.598\,\mathrm{m}</math></center> |
y en cartesianas | y en cartesianas | ||
| - | <math>x=1.061\,\mathrm{m}\qquad y = 1.061\,\mathrm{m}\qquad z = 2.598\,\mathrm{m}</math> | + | <center><math>x=1.061\,\mathrm{m}\qquad y = 1.061\,\mathrm{m}\qquad z = 2.598\,\mathrm{m}</math></center> |
Dos detalles importantes: | Dos detalles importantes: | ||
| Línea 64: | Línea 64: | ||
* El que un punto se exprese de forma sencilla en un sistema no implica que sea simple en otro diferente. | * El que un punto se exprese de forma sencilla en un sistema no implica que sea simple en otro diferente. | ||
| - | == | + | ==Enlaces== |
| - | [[Líneas y superficies coordenadas]] | + | * '''Siguiente:''' [[Líneas y superficies coordenadas]] |
| - | + | * '''Anterior:''' [[Coordenadas esféricas. Definición]] | |
| - | + | ||
| - | [[Coordenadas esféricas. Definición]] | + | |
| - | [[ | + | [[Categoría:Definición de sistemas|50]] |
última version al 11:39 23 nov 2007
Contenido |
1 Entre cartesianas y cilíndricas
mientras que las coordenadas 
e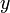 
constituyen los catetos de un triángulo rectángulo de hipotenusa 
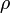, por lo que
De aquí se tienen las relaciones inversas
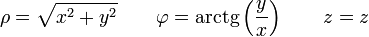
2 Entre cilíndricas y esféricas
Empleando de nuevo trigonometría podemos pasar de esféricas a cilíndricas. En primer lugar, la coordenada 
es la misma en los dos sistemas. El resto de coordenadas se relacionan mediante un nuevo triángulo rectángulo
y con las correspondientes relaciones inversas
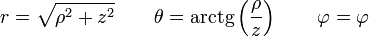
3 Entre cartesianas y esféricas
Combinando las relaciones anteriores obtenemos el paso de esféricas a cartesianas.
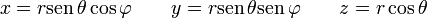
y sus correspondientes relaciones inversas
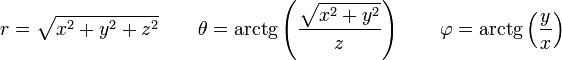
4 Algunos ejemplos numéricos
4.1 De cartesianas a otros sistemas
Supongamos que debemos dar las coordenadas cilíndricas y esféricas del punto dado, en cartesianas, por
La misma posición, en cilíndricas, se expresa
y, en esféricas,
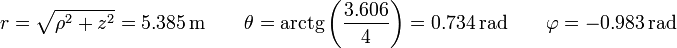
4.2 De esféricas a otros sistemas
Ahora supongamos que nos dan un punto, en esféricas, de coordenadas
Este mismo punto, en cilíndricas, es
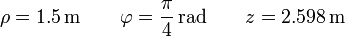
y en cartesianas
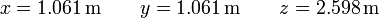
Dos detalles importantes:
- Las coordenadas poseen unidades.
- El que un punto se exprese de forma sencilla en un sistema no implica que sea simple en otro diferente.
5 Enlaces
- Siguiente: Líneas y superficies coordenadas
- Anterior: Coordenadas esféricas. Definición
