Espira parcialmente inmersa en un campo magnético
De Laplace
(Página creada con '==Enunciado== El campo entre los polos de un imán se puede modelar como un campo magnético uniforme <math>\vec{B}=B_0 \vec{k}</math> en el semiespacio <math>x>0</math>. Una es…') |
(→Caso |x| > a) |
||
| Línea 27: | Línea 27: | ||
<center><math>\vec{F}=\begin{cases}2I(a-|x|)B_0\vec{\imath} & (|x|\leq a) \\ | <center><math>\vec{F}=\begin{cases}2I(a-|x|)B_0\vec{\imath} & (|x|\leq a) \\ | ||
\vec{0}&(|x|>a)\end{cases}</math></center> | \vec{0}&(|x|>a)\end{cases}</math></center> | ||
| + | |||
| + | Gráficamente, queda en la forma: | ||
| + | |||
| + | <center>[[Archivo:F-espira-parcial.png|400px]]</center> | ||
última version al 19:51 21 may 2021
Contenido |
1 Enunciado
El campo entre los polos de un imán se puede modelar como un campo magnético uniforme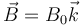 
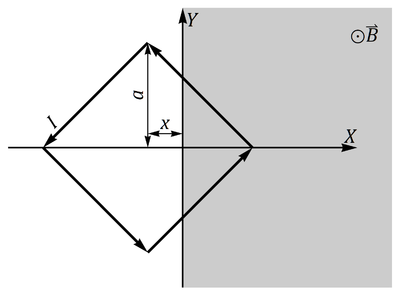
en el semiespacio x > 0. Una espira cuadrada se encuentra sumergida parcialmente en este campo. La espira se encuentra en el plano XY, girada 45° respecto a los ejes, de forma que su centro se halla en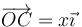 
(x puede ser tanto negativo como positivo). Por la espira circula una intensidad de corriente I. Calcule la fuerza sobre cada lado de la espira, así como la fuerza neta (distínga los casos necesarios en x).
2 Caso x <0
En general, cuando una espira está parcialmente inmersa en un campo magnético uniforme, la fueza sobre ella viene dada por
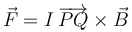
siendo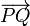 
el vector que va desde el punto donde entra la corriente al punto donde sale.
Cuando x < 0, es decir, cuando el centro de la espira aun no ha penetrado en el campo magnético, este vector es igual a la base del triángulo que tiene su vértice en el extremo de la derecha. Por ser los ángulos de 45°, la longitud de esta base es el doble de la altura correspondiente, que a su vez mide a − | x | (con valor absoluto porque x es negativo). Por tanto,
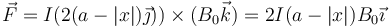
3 Caso x > 0
En este caso el razonamiento es idéntico, salvo que ahora la distancia PQ es la base del triángulo opuesto, formado con el vértice más a la izquierda. La base de este triángulo mide también 2(a − | x | ), por lo que la fuerza es, como en el caso anterior
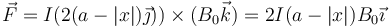
4 Caso |x| > a
Tanto si la espira no ha llegado a penetrar como si está completamente dentro del campo magnético uniforme, la fuerza magnética es nula.
Reuniendo los resultados, queda la fuerza magnética
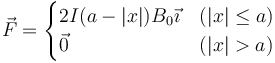
Gráficamente, queda en la forma:
