Problemas de campos magnéticos (GIOI)
De Laplace
(Diferencias entre revisiones)
(→Fuerza entre un hilo rectilíneo y una espira rectangular) |
|||
| (16 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
==Espira parcialmente inmersa en un campo magnético== | ==Espira parcialmente inmersa en un campo magnético== | ||
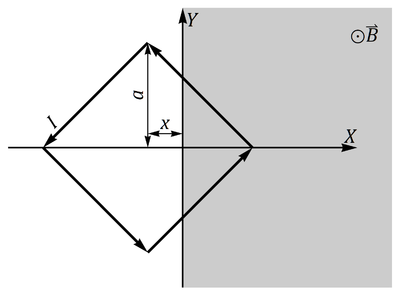
{{nivel|2}} El campo entre los polos de un imán se puede modelar como un campo magnético uniforme <math>\vec{B}=B_0 \vec{k}</math> en el semiespacio <math>x>0</math>. Una espira cuadrada se encuentra sumergida parcialmente en este campo. La espira se encuentra en el plano XY, girada 45° respecto a los ejes, de forma que su centro se halla en <math>\overrightarrow{OC}=x\vec{\imath}</math> (''x'' puede ser tanto negativo como positivo). Por la espira circula una intensidad de corriente ''I''. Calcule la fuerza sobre cada lado de la espira, así como la fuerza neta (distínga los casos necesarios en ''x''). | {{nivel|2}} El campo entre los polos de un imán se puede modelar como un campo magnético uniforme <math>\vec{B}=B_0 \vec{k}</math> en el semiespacio <math>x>0</math>. Una espira cuadrada se encuentra sumergida parcialmente en este campo. La espira se encuentra en el plano XY, girada 45° respecto a los ejes, de forma que su centro se halla en <math>\overrightarrow{OC}=x\vec{\imath}</math> (''x'' puede ser tanto negativo como positivo). Por la espira circula una intensidad de corriente ''I''. Calcule la fuerza sobre cada lado de la espira, así como la fuerza neta (distínga los casos necesarios en ''x''). | ||
| + | <center>[[Archivo:espira-parcial-campo.png|400px]]</center> | ||
[[Espira parcialmente inmersa en un campo magnético|'''Solución''']] | [[Espira parcialmente inmersa en un campo magnético|'''Solución''']] | ||
| + | |||
==Espira doble inmersa en un campo magnético== | ==Espira doble inmersa en un campo magnético== | ||
{{nivel|2}} Se tiene una espira doble cuyas dimensiones son las de la figura. Todas las varillas están hechas del mismo material con la misma sección. La espira está sumergida una distancia x en un campo magnético uniforme <math>\vec{B}=100\vec{k}\,(\mathrm{mT})</math>. El lado derecho de la espira es paralelo a la región ocupada por el campo magnético. Se sabe que por este lado circula una intensidad de corriente de 4 A. Calcule la fuerza magnética sobre la espira, como función de la distancia de penetración, ''x''. | {{nivel|2}} Se tiene una espira doble cuyas dimensiones son las de la figura. Todas las varillas están hechas del mismo material con la misma sección. La espira está sumergida una distancia x en un campo magnético uniforme <math>\vec{B}=100\vec{k}\,(\mathrm{mT})</math>. El lado derecho de la espira es paralelo a la región ocupada por el campo magnético. Se sabe que por este lado circula una intensidad de corriente de 4 A. Calcule la fuerza magnética sobre la espira, como función de la distancia de penetración, ''x''. | ||
| + | <center>[[Archivo:espira-doble-campo.png|400px]]</center> | ||
[[Espira doble inmersa en un campo magnético|'''Solución''']] | [[Espira doble inmersa en un campo magnético|'''Solución''']] | ||
| + | |||
==Espira girada dentro de un campo magnético== | ==Espira girada dentro de un campo magnético== | ||
| - | {{nivel|2}} Una espira rectangular ABCD se encuentra en el interior de un campo magnético uniforme \vec{B}=10\vec{k}\,(\mathrm{mT}). Los vértices de la espira se encuentran en | + | {{nivel|2}} Una espira rectangular ABCD se encuentra en el interior de un campo magnético uniforme <math>\vec{B}=10\vec{k}\,(\mathrm{mT})</math>. Los vértices de la espira se encuentran en |
<center><math>\vec{r}_A=3\vec{\imath}-5\vec{\jmath}-4\vec{k}\qquad\qquad\vec{r}_B=3\vec{\imath}+5\vec{\jmath}-4\vec{k}\qquad\qquad \vec{r}_C=-3\vec{\imath}+5\vec{\jmath}+4\vec{k}\qquad\qquad\vec{r}_D=-3\vec{\imath}-5\vec{\jmath}+4\vec{k}</math></center> | <center><math>\vec{r}_A=3\vec{\imath}-5\vec{\jmath}-4\vec{k}\qquad\qquad\vec{r}_B=3\vec{\imath}+5\vec{\jmath}-4\vec{k}\qquad\qquad \vec{r}_C=-3\vec{\imath}+5\vec{\jmath}+4\vec{k}\qquad\qquad\vec{r}_D=-3\vec{\imath}-5\vec{\jmath}+4\vec{k}</math></center> | ||
(distancias medidas en cm). Por la espira circula una corriente de 0.2 A en el sentido ABCD. | (distancias medidas en cm). Por la espira circula una corriente de 0.2 A en el sentido ABCD. | ||
# Halle la fuerza magnética sobre cada lado de la espira, así como la fuerza total sobre la espira | # Halle la fuerza magnética sobre cada lado de la espira, así como la fuerza total sobre la espira | ||
| - | # Considerando cada fuerza aplicada sobre el centro del lado correspondiente, halle el momento resultante, según la ley | + | # Considerando cada fuerza aplicada sobre el centro del lado correspondiente, halle el momento resultante, según la ley <math>\vec{M}_G=\sum_i\overrightarrow{OP}_i\times\vec{F}_i</math> |
| - | <math>\vec{M}_G=\sum_i\overrightarrow{OP}_i\times\vec{F}_i</math> | + | |
# Calcule el momento magnético de la espira <math>\vec{m}=IS\vec{n}</math> y compruebe que <math>\vec{M}_G=\vec{m}\times\vec{B}</math> | # Calcule el momento magnético de la espira <math>\vec{m}=IS\vec{n}</math> y compruebe que <math>\vec{M}_G=\vec{m}\times\vec{B}</math> | ||
[[Espira girada dentro de un campo magnético|'''Solución''']] | [[Espira girada dentro de un campo magnético|'''Solución''']] | ||
| + | |||
==Campo magnético debido a un segmento== | ==Campo magnético debido a un segmento== | ||
| - | {{nivel|3}} Halle el campo magnético producido por un segmento rectilíneo, por el cual circula una intensidad de corriente <math>I_0</math>, en cualquier punto del espacio. Para fijar ideas, sitúese el punto de medición del campo en <math>\overrightarrow{OP}=\vec{r}=x\vec{\imath} </math>y el segmento sobre el eje OZ extendiéndose desde \overrightarrow{ | + | {{nivel|3}} Halle el campo magnético producido por un segmento rectilíneo, por el cual circula una intensidad de corriente <math>I_0</math>, en cualquier punto del espacio. Para fijar ideas, sitúese el punto de medición del campo en <math>\overrightarrow{OP}=\vec{r}=x\vec{\imath} </math>y el segmento sobre el eje OZ extendiéndose desde <math>\overrightarrow{OA}=z_1 \vec{k}</math> a <math>\overrightarrow{OB}=z_2 \vec{k}</math> (con la corriente de A a B). Posteriormente generalícese el resultado, con ayuda de las coordenadas cilíndricas. |
[[Campo magnético debido a un segmento|'''Solución''']] | [[Campo magnético debido a un segmento|'''Solución''']] | ||
| + | |||
==Campo magnético debido a un hilo infinito== | ==Campo magnético debido a un hilo infinito== | ||
| - | {{nivel|1}} A partir del resultado del problema “[[Campo magnético debido a un segmento]]” calcule, para todos los puntos del espacio, el campo magnético creado por un hilo rectilíneo infinitamente largo situado sobre el eje OZ y por el cual circula una corriente I_0 en el sentido del eje OZ positivo. | + | {{nivel|1}} A partir del resultado del problema “[[Campo magnético debido a un segmento]]” calcule, para todos los puntos del espacio, el campo magnético creado por un hilo rectilíneo infinitamente largo situado sobre el eje OZ y por el cual circula una corriente <math>I_0</math> en el sentido del eje OZ positivo. |
[[Campo magnético debido a un hilo infinito|'''Solución''']] | [[Campo magnético debido a un hilo infinito|'''Solución''']] | ||
| + | |||
==Campo magnético debido a dos hilos paralelos== | ==Campo magnético debido a dos hilos paralelos== | ||
{{nivel|3}} Dos hilos paralelos se hallan situados paralelamente al eje OZ, situados sobre x=±a, y=0. Determine el valor del campo magnético en todos los puntos del plano x=0, y en todos los puntos del plano y=0 en los dos casos siguientes: | {{nivel|3}} Dos hilos paralelos se hallan situados paralelamente al eje OZ, situados sobre x=±a, y=0. Determine el valor del campo magnético en todos los puntos del plano x=0, y en todos los puntos del plano y=0 en los dos casos siguientes: | ||
| Línea 30: | Línea 36: | ||
# Por los hilos circulan corrientes antiparalelas <math>\pm I_0</math>. | # Por los hilos circulan corrientes antiparalelas <math>\pm I_0</math>. | ||
# Para el caso particular <math>a=2\,\mathrm{cm}</math> <math>I_0=0.1\,\mathrm{A}</math> , ¿cuánto vale el campo magnético en el origen de coordenadas para los dos casos anteriores? | # Para el caso particular <math>a=2\,\mathrm{cm}</math> <math>I_0=0.1\,\mathrm{A}</math> , ¿cuánto vale el campo magnético en el origen de coordenadas para los dos casos anteriores? | ||
| - | # ¿Cuánto vale la fuerza magnética que uno de los hilos ejerce sobre una porción de longitud | + | # ¿Cuánto vale la fuerza magnética que uno de los hilos ejerce sobre una porción de longitud ℓ del otro? |
[[Campo magnético debido a dos hilos paralelos|'''Solución''']] | [[Campo magnético debido a dos hilos paralelos|'''Solución''']] | ||
| Línea 40: | Línea 46: | ||
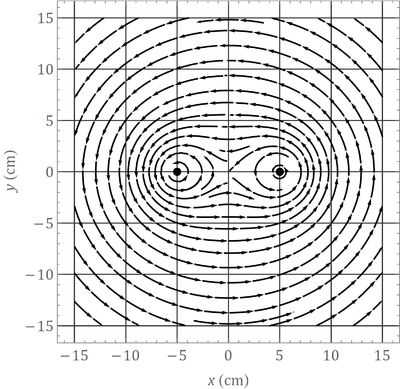
* Dos corrientes paralelas de valores <math>I_1=8\,\mathrm{A}</math>, <math>I_2=2\,\mathrm{A}</math> | * Dos corrientes paralelas de valores <math>I_1=8\,\mathrm{A}</math>, <math>I_2=2\,\mathrm{A}</math> | ||
* Dos corrientes antiparalelas de valores <math>I_1=8\,\mathrm{A}</math>, <math>I_2=2\,\mathrm{A}</math> | * Dos corrientes antiparalelas de valores <math>I_1=8\,\mathrm{A}</math>, <math>I_2=2\,\mathrm{A}</math> | ||
| - | + | ||
| + | {| class="bordeado" | ||
| + | |- | ||
| + | | [[Archivo:graf-campoB-01.png|400px]] | ||
| + | | [[Archivo:graf-campoB-02.png|400px]] | ||
| + | |- | ||
| + | | (a) | ||
| + | | (b) | ||
| + | |- | ||
| + | | [[Archivo:graf-campoB-03.png|400px]] | ||
| + | | [[Archivo:graf-campoB-04.png|400px]] | ||
| + | |- | ||
| + | | (c) | ||
| + | | (d) | ||
| + | |} | ||
| + | |||
Para este sistema de dos hilos, ¿en qué punto se anula el campo magnético, para <math>I_1</math> e <math>I_2</math> cualesquiera? | Para este sistema de dos hilos, ¿en qué punto se anula el campo magnético, para <math>I_1</math> e <math>I_2</math> cualesquiera? | ||
| Línea 47: | Línea 68: | ||
==Mapa del campo magnético de dos hilos paralelos== | ==Mapa del campo magnético de dos hilos paralelos== | ||
{{nivel|1}} Para un sistema de dos hilos paralelos de gran longitud situados en x=±5\,cm el campo magnético en el plano OXY tiene una cierta distribución de líneas de campo. Indique cuál de las cuatro figuras siguientes corresponde a la gráfica de B(x) en los casos siguientes: | {{nivel|1}} Para un sistema de dos hilos paralelos de gran longitud situados en x=±5\,cm el campo magnético en el plano OXY tiene una cierta distribución de líneas de campo. Indique cuál de las cuatro figuras siguientes corresponde a la gráfica de B(x) en los casos siguientes: | ||
| - | * Dos corrientes paralelas (en el mismo sentido) de valor <math>I_1=I_2=5\,A</math>. | + | * Dos corrientes paralelas (en el mismo sentido) de valor <math>I_1=I_2=5\,\mathrm{A}</math>. |
| - | * Dos corrientes antiparalelas (en sentido opuesto) de valor I_1=I_2=5\,A. | + | * Dos corrientes antiparalelas (en sentido opuesto) de valor <math>I_1=I_2=5\,\mathrm{A}</math>. |
| - | * Dos corrientes paralelas de valores I_1= | + | * Dos corrientes paralelas de valores <math>I_1=5\,\mathrm{A}</math>, <math>I_2=3\,\mathrm{A}</math> |
| - | * Dos corrientes antiparalelas de valores I_1= | + | * Dos corrientes antiparalelas de valores <math>I_1=5\,\mathrm{A}</math>, <math>I_2=3\,\mathrm{A}</math> |
| + | |||
| + | {| class="bordeado" | ||
| + | |- | ||
| + | | [[Archivo:mapa-campoB-01.png|400px]] | ||
| + | | [[Archivo:mapa-campoB-02.png|400px]] | ||
| + | |- | ||
| + | | (a) | ||
| + | | (b) | ||
| + | |- | ||
| + | | [[Archivo:mapa-campoB-03.png|400px]] | ||
| + | | [[Archivo:mapa-campoB-04.png|400px]] | ||
| + | |- | ||
| + | | (c) | ||
| + | | (d) | ||
| + | |} | ||
| + | |||
[[Mapa del campo magnético de dos hilos paralelos|'''Solución''']] | [[Mapa del campo magnético de dos hilos paralelos|'''Solución''']] | ||
| + | |||
==Campo magnético en el centro de un rectángulo== | ==Campo magnético en el centro de un rectángulo== | ||
{{nivel|3}} partir del resultado del problema “[[Campo magnético debido a un segmento]]”, halle el campo magnético en el centro de una espira rectangular de lados b y h por la cual circula una corriente <math>I_0</math>. | {{nivel|3}} partir del resultado del problema “[[Campo magnético debido a un segmento]]”, halle el campo magnético en el centro de una espira rectangular de lados b y h por la cual circula una corriente <math>I_0</math>. | ||
| Línea 63: | Línea 101: | ||
[[Campo magnético en el centro de un polígono|'''Solución''']] | [[Campo magnético en el centro de un polígono|'''Solución''']] | ||
==Campo magnético en el eje de una espira circular== | ==Campo magnético en el eje de una espira circular== | ||
| - | {{nivel|4}} Halle, por integración directa, el campo magnético en los puntos del eje de una espira circular de radio b, por la cual circula una corriente I_0. ¿Cuánto vale aproximadamente este campo en puntos alejados (<math>z\gg b</math>)? | + | {{nivel|4}} Halle, por integración directa, el campo magnético en los puntos del eje de una espira circular de radio b, por la cual circula una corriente <math>I_0</math>. ¿Cuánto vale aproximadamente este campo en puntos alejados (<math>z\gg b</math>)? |
[[Campo magnético en el eje de una espira circular|'''Solución''']] | [[Campo magnético en el eje de una espira circular|'''Solución''']] | ||
| + | |||
==Campo magnético en el eje de una bobina cilíndrica== | ==Campo magnético en el eje de una bobina cilíndrica== | ||
{{nivel|4}}A partir del caso anterior, calcule el campo magnético debido a una bobina de longitud h y radio b con N espiras. ¿A qué tiende el resultado cuando <math>h\gg b</math>? | {{nivel|4}}A partir del caso anterior, calcule el campo magnético debido a una bobina de longitud h y radio b con N espiras. ¿A qué tiende el resultado cuando <math>h\gg b</math>? | ||
| Línea 71: | Línea 110: | ||
[[Campo magnético en el eje de una bobina cilíndrica|'''Solución''']] | [[Campo magnético en el eje de una bobina cilíndrica|'''Solución''']] | ||
==Campo magnético de un sistema de tres hilos== | ==Campo magnético de un sistema de tres hilos== | ||
| - | {{nivel|3}} Se tiene un sistema formado por tres hilos de constantán, una aleación que tiene conductividad <math>\sigma=2.0\times10^6\,\mathrm{S}/\mathrm{m}</math>, los tres hilos son de la misma longitud, <math>\ell=12\,\mathrm{m}</math>. El hilo “1” tiene una sección transversal <math>A_1=3\,\mathrm{mm}^2</math>, el “2” una sección <math>A_2=1\,\mathrm{mm}^2</math> y el “3” una sección <math>A_3=2\,\mathrm{mm}^2</math>. Se disponen paralelamente, con una distancia entre ellos <math>b=10\,\mathrm{cm}</math>. Se conectan como indica la figura, con los interruptores A y B cerrados. Tanto los interruptores como las demás conexiones son ideales, sin resistencia. El hilo “1” se conecta a una fuente de tensión continua V_0=13.2\,V y el “3” a tierra. | + | {{nivel|3}} Se tiene un sistema formado por tres hilos de constantán, una aleación que tiene conductividad <math>\sigma=2.0\times10^6\,\mathrm{S}/\mathrm{m}</math>, los tres hilos son de la misma longitud, <math>\ell=12\,\mathrm{m}</math>. El hilo “1” tiene una sección transversal <math>A_1=3\,\mathrm{mm}^2</math>, el “2” una sección <math>A_2=1\,\mathrm{mm}^2</math> y el “3” una sección <math>A_3=2\,\mathrm{mm}^2</math>. Se disponen paralelamente, con una distancia entre ellos <math>b=10\,\mathrm{cm}</math>. Se conectan como indica la figura, con los interruptores A y B cerrados. Tanto los interruptores como las demás conexiones son ideales, sin resistencia. El hilo “1” se conecta a una fuente de tensión continua <math>V_0=13.2\,\mathrm{V}</math> y el “3” a tierra. |
| - | + | ||
| + | <center>[[Archivo:tres-hilos-campoB.png|600px]]</center> | ||
Se trata de comparar el estado de corriente continua antes de que se abran los interruptores y el estado de corriente continua después de abrir ambos. | Se trata de comparar el estado de corriente continua antes de que se abran los interruptores y el estado de corriente continua después de abrir ambos. | ||
Halle el campo magnético en los puntos P y Q, situados en los puntos medios entre los hilos “1” y “2”, y entre “2” y “3”. | Halle el campo magnético en los puntos P y Q, situados en los puntos medios entre los hilos “1” y “2”, y entre “2” y “3”. | ||
| Línea 79: | Línea 119: | ||
[[Campo magnético de un sistema de tres hilos|'''Solución''']] | [[Campo magnético de un sistema de tres hilos|'''Solución''']] | ||
| + | |||
==Fuerza entre un hilo rectilíneo y una espira rectangular== | ==Fuerza entre un hilo rectilíneo y una espira rectangular== | ||
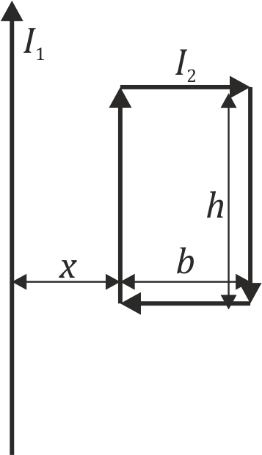
{{nivel|3}} Junto a un hilo rectilíneo por el cual circula una intensidad de corriente <math>I_1</math>, que podemos situar en el eje OZ, se encuentra una espira rectangular de base b y altura h, situada en el plano OXZ con dos de sus lados paralelos al hilo. El lado más próximo se encuentra a una distancia x del hilo. Por la espira rectangular circula una intensidad de corriente <math>I_2</math>. | {{nivel|3}} Junto a un hilo rectilíneo por el cual circula una intensidad de corriente <math>I_1</math>, que podemos situar en el eje OZ, se encuentra una espira rectangular de base b y altura h, situada en el plano OXZ con dos de sus lados paralelos al hilo. El lado más próximo se encuentra a una distancia x del hilo. Por la espira rectangular circula una intensidad de corriente <math>I_2</math>. | ||
# ¿Qué fuerza ejerce el hilo rectilíneo sobre la espira rectangular? | # ¿Qué fuerza ejerce el hilo rectilíneo sobre la espira rectangular? | ||
# ¿A qué tiende esta fuerza en el límite <math>b\to 0</math>,<math>h\to 0</math>, <math>I_2\to\infty</math> con <math>I_2 bh\to m</math>? | # ¿A qué tiende esta fuerza en el límite <math>b\to 0</math>,<math>h\to 0</math>, <math>I_2\to\infty</math> con <math>I_2 bh\to m</math>? | ||
| + | |||
| + | <center>[[Archivo:hilo-espira-rectangular.png]]</center> | ||
[[Fuerza entre un hilo rectilíneo y una espira rectangular|'''Solución''']] | [[Fuerza entre un hilo rectilíneo y una espira rectangular|'''Solución''']] | ||
última version al 19:48 20 may 2021
1 Espira parcialmente inmersa en un campo magnético
El campo entre los polos de un imán se puede modelar como un campo magnético uniforme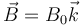 
en el semiespacio x > 0. Una espira cuadrada se encuentra sumergida parcialmente en este campo. La espira se encuentra en el plano XY, girada 45° respecto a los ejes, de forma que su centro se halla en 
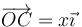(x puede ser tanto negativo como positivo). Por la espira circula una intensidad de corriente I. Calcule la fuerza sobre cada lado de la espira, así como la fuerza neta (distínga los casos necesarios en x).
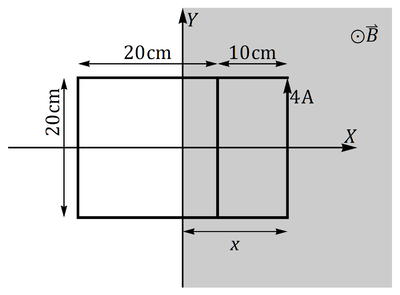
2 Espira doble inmersa en un campo magnético
Se tiene una espira doble cuyas dimensiones son las de la figura. Todas las varillas están hechas del mismo material con la misma sección. La espira está sumergida una distancia x en un campo magnético uniforme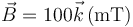 
. El lado derecho de la espira es paralelo a la región ocupada por el campo magnético. Se sabe que por este lado circula una intensidad de corriente de 4 A. Calcule la fuerza magnética sobre la espira, como función de la distancia de penetración, x.
3 Espira girada dentro de un campo magnético
Una espira rectangular ABCD se encuentra en el interior de un campo magnético uniforme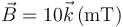 
. Los vértices de la espira se encuentran en
(distancias medidas en cm). Por la espira circula una corriente de 0.2 A en el sentido ABCD.
- Halle la fuerza magnética sobre cada lado de la espira, así como la fuerza total sobre la espira
- Considerando cada fuerza aplicada sobre el centro del lado correspondiente, halle el momento resultante, según la ley
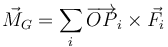
- Calcule el momento magnético de la espira
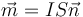y compruebe que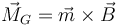 
4 Campo magnético debido a un segmento
Halle el campo magnético producido por un segmento rectilíneo, por el cual circula una intensidad de corriente I0, en cualquier punto del espacio. Para fijar ideas, sitúese el punto de medición del campo en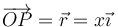 
y el segmento sobre el eje OZ extendiéndose desde 
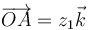a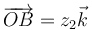 
(con la corriente de A a B). Posteriormente generalícese el resultado, con ayuda de las coordenadas cilíndricas.
5 Campo magnético debido a un hilo infinito
A partir del resultado del problema “Campo magnético debido a un segmento” calcule, para todos los puntos del espacio, el campo magnético creado por un hilo rectilíneo infinitamente largo situado sobre el eje OZ y por el cual circula una corriente I0 en el sentido del eje OZ positivo.
6 Campo magnético debido a dos hilos paralelos
Dos hilos paralelos se hallan situados paralelamente al eje OZ, situados sobre x=±a, y=0. Determine el valor del campo magnético en todos los puntos del plano x=0, y en todos los puntos del plano y=0 en los dos casos siguientes:
- Por los hilos circulan corrientes paralelas + I0.
- Por los hilos circulan corrientes antiparalelas
.
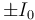- Para el caso particular
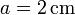
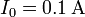, ¿cuánto vale el campo magnético en el origen de coordenadas para los dos casos anteriores?
- ¿Cuánto vale la fuerza magnética que uno de los hilos ejerce sobre una porción de longitud ℓ del otro?
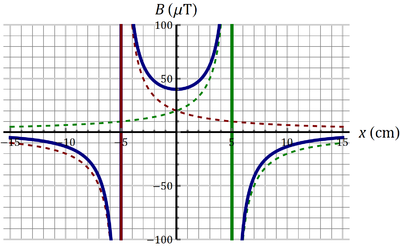
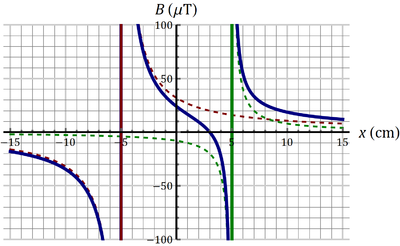
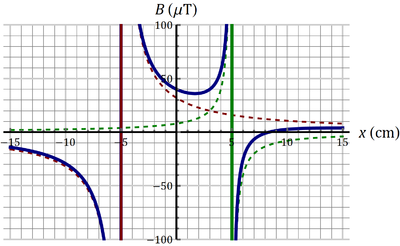
7 Gráfica del campo magnético de dos hilos paralelos
Para un sistema de dos hilos paralelos de gran longitud situados en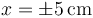 
el campo magnético en los puntos de OX es de la forma 
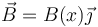Indique cuál de las cuatro figuras siguientes corresponde a la gráfica de B(x) en los casos siguientes:
- Dos corrientes paralelas (en el mismo sentido) de valor
.
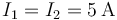- Dos corrientes antiparalelas (en sentido opuesto) de valor .
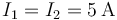- Dos corrientes paralelas de valores
, 
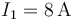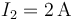
- Dos corrientes antiparalelas de valores ,
| 
|
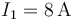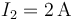
| (a) | (b) |
| 
|
| (c) | (d) |
Para este sistema de dos hilos, ¿en qué punto se anula el campo magnético, para I1 e I2 cualesquiera?
8 Mapa del campo magnético de dos hilos paralelos
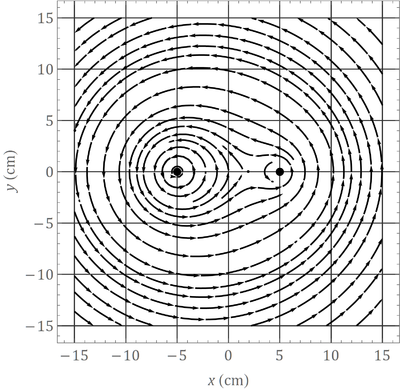
Para un sistema de dos hilos paralelos de gran longitud situados en x=±5\,cm el campo magnético en el plano OXY tiene una cierta distribución de líneas de campo. Indique cuál de las cuatro figuras siguientes corresponde a la gráfica de B(x) en los casos siguientes:
- Dos corrientes paralelas (en el mismo sentido) de valor .
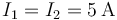- Dos corrientes antiparalelas (en sentido opuesto) de valor .
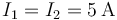- Dos corrientes paralelas de valores
, 
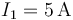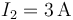
- Dos corrientes antiparalelas de valores ,
| 
|
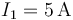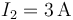
| (a) | (b) |
| 
|
| (c) | (d) |
9 Campo magnético en el centro de un rectángulo
partir del resultado del problema “Campo magnético debido a un segmento”, halle el campo magnético en el centro de una espira rectangular de lados b y h por la cual circula una corriente I0.
10 Campo magnético en el centro de un polígono
partir del resultado del problema “Campo magnético debido a un segmento” halle el campo magnético en el centro de un polígono regular de N lados y apotema b, por el cual circula una intensidad de corriente I0. ¿A qué tiende este resultado en el caso de una espira circular (N→∞)?
11 Campo magnético en el eje de una espira circular
Halle, por integración directa, el campo magnético en los puntos del eje de una espira circular de radio b, por la cual circula una corriente I0. ¿Cuánto vale aproximadamente este campo en puntos alejados (
)?
12 Campo magnético en el eje de una bobina cilíndrica
A partir del caso anterior, calcule el campo magnético debido a una bobina de longitud h y radio b con N espiras. ¿A qué tiende el resultado cuando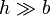 
?
13 Campo magnético de un sistema de tres hilos
Se tiene un sistema formado por tres hilos de constantán, una aleación que tiene conductividad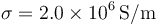 
, los tres hilos son de la misma longitud, 
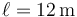. El hilo “1” tiene una sección transversal 
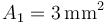, el “2” una sección 
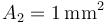y el “3” una sección 
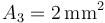. Se disponen paralelamente, con una distancia entre ellos 
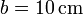. Se conectan como indica la figura, con los interruptores A y B cerrados. Tanto los interruptores como las demás conexiones son ideales, sin resistencia. El hilo “1” se conecta a una fuente de tensión continua 
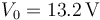y el “3” a tierra.
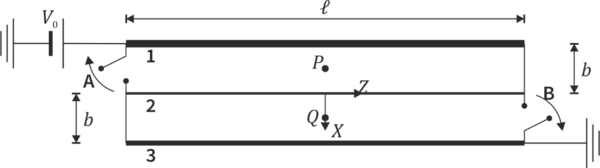
Se trata de comparar el estado de corriente continua antes de que se abran los interruptores y el estado de corriente continua después de abrir ambos. Halle el campo magnético en los puntos P y Q, situados en los puntos medios entre los hilos “1” y “2”, y entre “2” y “3”.
- Con los dos interruptores cerrados.
- Con los dos interruptores abiertos.
14 Fuerza entre un hilo rectilíneo y una espira rectangular
Junto a un hilo rectilíneo por el cual circula una intensidad de corriente I1, que podemos situar en el eje OZ, se encuentra una espira rectangular de base b y altura h, situada en el plano OXZ con dos de sus lados paralelos al hilo. El lado más próximo se encuentra a una distancia x del hilo. Por la espira rectangular circula una intensidad de corriente I2.
- ¿Qué fuerza ejerce el hilo rectilíneo sobre la espira rectangular?
- ¿A qué tiende esta fuerza en el límite
,
, 
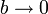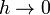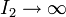con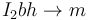 
?
