Tres masas en un triángulo (CMR)

De Laplace

Revisión de 17:32 11 ene 2021

1 Tres masas en un triángulo

Un sólido rígido está formado por tres masas: una 5m, situada en O(0,0,0), una 4m, en A(3b,0,0) y una 3m, en B(0,4b,0).

1. ¿En qué posición se encuentra el centro de masas del sistema?
2. ¿Cuánto vale el tensor de inercia de este sólido respecto a unos ejes paralelos a OX, OY y OZ, por el centro de masas?
3. Si el sólido está girando en torno a un eje que pasa por el CM y con velocidad angular , calcule cuánto valen
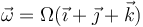
   1. su momento cinético respecto a G.
   2. su momento cinético respecto a O.
   3. su energía cinética.

2 Centro de masas

La posición del CM es la media ponderada de las posiciones de las tres masas

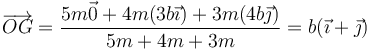
3 Tensor de inercia

Para hallar el tensor de inercia tenemos dos caminos.

• Directamente mediante las posiciones de las tres partículas respecto a los nuevos ejes.
• Hallando primero el tensor respecto a unos ejes por O y posteriormente aplicar el teorema de Steiner.

Veámoslo de las dos formas.

3.1 Directamente

La posición de las tres masas respecto al CM es, para O

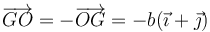
para A

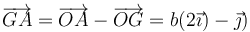
y para B

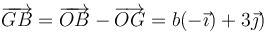
Aplicamos ahora la definición de tensor de inercia

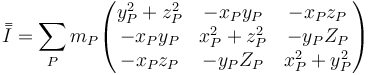
queda para la masa de O, de valor 5m

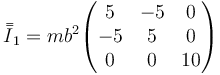
Para la de A, de valor 4m

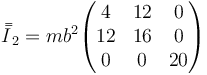
y para la de C, de valor 3M

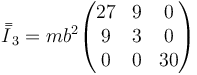
Sumando los tres tensores

Este sería el código que lo hace en Mathematica (muy poco optimizado, pero para que se entienda mejor)

J[m_, P_] := m (P . P IdentityMatrix[3] - KroneckerProduct[P, P])

lm = {5 m, 4 m, 3 m}

OP = {{0, 0, 0}, {3 b, 0, 0}, {0, 4 b, 0}}

OG = Sum[lm[[i]] OP[[i]], {i, 3}]/Sum[lm[[i]], {i, 3}]

GP = Table[OP[[i]] - OG, {i, 3}]

Sum[J[lm[[i]], GP[[i]]], {i, 3}] // MatrixForm