Partículas en colisión inelástica unidireccional
De Laplace
(Página creada con '= Enunciado = Una partícula de masa <math>m</math> y velocidad <math>\vec{v}_0</math> colisiona con otra partícula de masa <math>m</math> que está en reposo. Después del cho…') |
(→Solución) |
||
| Línea 81: | Línea 81: | ||
</math> | </math> | ||
</center> | </center> | ||
| + | |||
| + | [[Categoría:Problemas de dinámica de un sistema de partículas|0]] | ||
| + | [[Categoría:Dinámica de un sistema de partículas|1]] | ||
última version al 14:58 11 ene 2021
1 Enunciado
Una partícula de masa m y velocidad  colisiona con otra partícula de masa m que está en reposo. Después del choque las dos partículas se mueven en la dirección de
colisiona con otra partícula de masa m que está en reposo. Después del choque las dos partículas se mueven en la dirección de  . El coeficiente de restitución del choque es CR.
. El coeficiente de restitución del choque es CR.
- Determina la velocidad de las dos partículas después del choque.
- Calcula la pérdida de energía cinética en función del valor del coeficiente de restitución. ¿Cómo es la variación de energía cinética en los valores límites del coeficiente de restitución?
2 Solución
Escogemos el eje X en la dirección que coincide con la velocidad de la partícula que se mueve antes de la colisión. Antes de la colisión tenemos

Después de la colisión las velocidades de las partículas son

En toda colisión se conserva la cantidad de movimiento, pues las fuerzas externas no tienen tiempo de cambiarla debido a que ocurre muy rápido. Como las partículas tienen la misma masa m tenemos
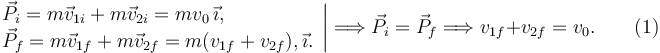
Necesitamos otra ecuación. Esta la proporciona el coeficiente de restitución. Su definición es
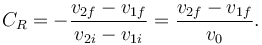
Hemos usado que en este problema v1i = v0 y v2i = 0. Esto nos da la otra ecuación
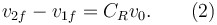
Despejando obtenemos
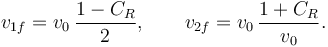
Podemos evaluar la pérdida de energía cinética que sufre el sistema de dos partículas
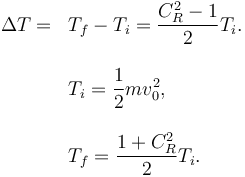
Los casos extremos son
CR = 1
Esto corresponde a una colisión elástica. Tenemos
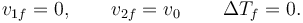
CR = 0
Esto corresponde a una colisión completamente inelástica (plástica). Tenemos