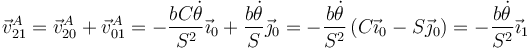Barra apoyada en placa cuadrada (CMR)

De Laplace

(Diferencias entre revisiones)

Revisión de 21:24 7 dic 2020

Contenido

1 Enunciado
2 Centros instantáneos de rotación
3 Velocidad de A

1 Enunciado

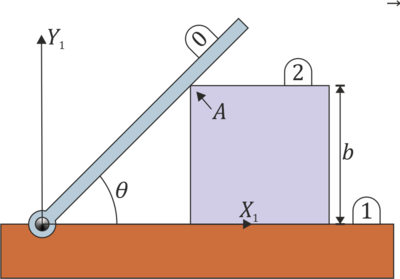
El esquema de la figura muestra una placa cuadrada de lado b (sólido “2”), uno de cuyos lados desliza sobre el eje horizontal fijo $O X 1$ (sólido “1”), mientras que la placa permanece contenida siempre en el plano vertical fijo $O X 1 Y 1$ . Sobre el vértice A de dicha placa se apoya en todo instante una varilla delgada (sólido “0”), que gira con velocidad angular 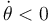$\dot{\theta}̇<0$ , alrededor de su extremo articulado en el punto fijo O (ver figura).

Determine gráficamente la posición de los centros instantáneos de rotación $I 21$ , $I 02$ e $I 01$ .
Calcule la velocidad del vértice A de la placa en el movimiento de ésta respecto de los ejes fijos y respecto de la barra (movimientos {21} y {20}, respectivamente), expresada en función de θ y sus derivadas,
Halle la velocidad angular $\vec{\omega}_{20}$ , correspondiente al movimiento relativo de la placa respecto de la varilla (movimiento {20}).
Determine analíticamente y geométricamente la posición del CIR del movimiento {20} (en función del ángulo θ).

2 Centros instantáneos de rotación

2.1 Del movimiento {01}

Puesto que la barra gira en torno a la articulación O, éste es ek CIR de este movimiento

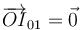
$\overrightarrow{OI}_{01}=\vec{0}\,$

2.2 Del movimiento {21}

La placa realiza un movimiento de traslación sobre el eje OX, por tanto su centro instantáneo de rotación se halla en el infinito, pero no en cualquier lugar, sino en una dirección perpendicular a la dirección de movimiento, es decir, abusando de la notación

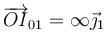
$\overrightarrow{OI}_{01}=\infty\vec{\jmath}_1\,$

2.3 Del movimiento {20}

Este requiere algún cálculo. Debe estar alineado con los otros dos, por lo que debe encontrarse sobre el eje $O X 1$ . Para hallar el punto exacto, buscamos la velocidad de un punto concreto y trazamos la perpendicular.

Consideremos el punto A, en el que la barra se apoya en la placa. Este punto de la placa “2” está deslizando sobre la barra “0” por lo que la velocidad de este punto en este movimiento es de la forma

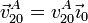
$\vec{v}^A_{20}=v^A_{20}\vec{\imath}_0$

siendo el eje $O X 0$ el que va a lo largo de la placa. La relación entre las bases es

$\vec{\imath}_0=C\vec{\imath}_1+S\vec{\jmath}_1\qquad\qquad \vec{\jmath}_0=-S\vec{\imath}_1+C\vec{\jmath}_1$

Gráficamente, el centro $I 20$ se encuentra en la intersección de esta perpendicular con el eje vertical.

Para hallar las coordenadas de este punto, observamos que la perpendicular a la velocidad la marca el vector 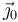$\vec{\jmath}_0$ . Por tanto el CIR se encontrará en un punto de la forma

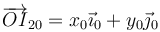
$\overrightarrow{OI}_{20}=x_0\vec{\imath}_0+y_0\vec{\jmath}_0$

y, al mismo tiempo, puesto que se encuentra sobre el eje vertical

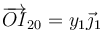
$\overrightarrow{OI}_{20}=y_1\vec{\jmath}_1$

Estas dos expresiones deben ser coincidentes.

El valor de $x 0$ lo obtenemos por simple trigonometría. Si b es la altura de la placa, la distancia OA mide

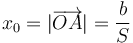
$x_0=|\overrightarrow{OA}|=\frac{b}{S}$

donde, como en otras ocasiones, $C = cos(θ)$ , $S = sen(θ)$ .

Tenemos entonces la igualdad

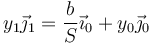
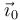
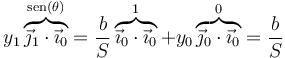
$y_1\vec{\jmath}_1=\frac{b}{S}\vec{\imath}_0+y_0\vec{\jmath}_0$ Si proyectamos sobre $\vec{\imath}_0$ $y_1\overbrace{\vec{\jmath}_1\cdot\vec{\imath}_0}^{\mathrm{sen}(\theta)}=\frac{b}{S}\overbrace{\vec{\imath}_0\cdot\vec{\imath}_0}^{1}+y_0\overbrace{\vec{\jmath}_0\cdot\vec{\imath}_0}^{0}=\frac{b}{S}$

lo que nos da

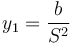
$y_1=\frac{b}{S^2}$

y

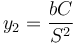
$y_2=\frac{bC}{S^2}$

También se puede llegar a este resultado con un poco más de trigonometría observando que $O A I 20$ es un triángulo rectángulo con ángulo en el vértice O de 90&degree;−θ.

3 Velocidad de A

3.1 Primer método

En el movimiento {01}, A, como punto de la barra, efectúa una rotación en torno a O, por lo que su velocidad es

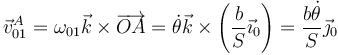
$\vec{v}^A_{01}=\omega_{01}\vec{k}\times\overrightarrow{OA}=\dot{\theta}\vec{k}\times\left(\frac{b}{S}\vec{\imath}_0\right)=\frac{b\dot{\theta}}{S}\vec{\jmath}_0$

En el movimiento {21} el movimiento es puramente horizontal y en el {20} es a lo largo de la barra, por lo que de la ley de composición

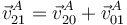
$\vec{v}^A_{21}=\vec{v}^A_{20}+\vec{v}^A_{01}$

queda

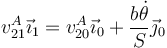
$v^A_{21}\vec{\imath}_1=v^A_{20}\vec{\imath}_0+\frac{b\dot{\theta}}{S}\vec{\jmath}_0$

Proyectando sobre 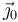$\vec{\jmath}_0$ queda

$-v^A_{21}S = \frac{b\dot{\theta}}{S}\qquad\Rightarrow\qquad v^A_{21}=-\frac{b\dot{\theta}}{S^2}$

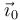
y sobre $\vec{\imath}_0$

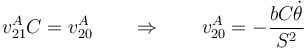
$v^A_{21}C = v^A_{20}\qquad\Rightarrow\qquad v^A_{20}=-\frac{bC\dot{\theta}}{S^2}$

También se puede llegar a este resultado expresando

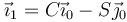
$\vec{\imath}_1=C\vec{\imath}_0-S\vec{\jmath}_0$

y luego igualando componente a componente.

3.2 Segundo método

Pueden calcularse estas velocidades directamente hallando la posición de A y derivando. En el sistema 1

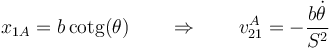
$x_{1A}=b\,\mathrm{cotg}(\theta)\qquad\Rightarrow\qquad v^A_{21}=-\frac{b\dot{\theta}}{S^2}$

En el sistema 0

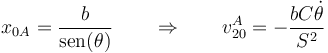
$x_{0A}=\frac{b}{\mathrm{sen}(\theta)}\qquad\Rightarrow\qquad v^A_{20}=-\frac{bC\dot{\theta}}{S^2}$

3.3 Tercer método

También puede hallarse con ayuda del CIR calculado antes. En el movimiento {20} A efectúa una rotación en torno a $I 20$ , por lo que

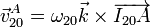
$\vec{v}^A_{20}=\omega_{20}\vec{k}\times\overrightarrow{I_{20}A}$

siendo

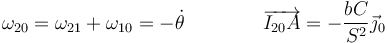
$\omega_{20}=\omega_{21}+\omega_{10}=-\dot{\theta}\qquad\qquad \overrightarrow{I_{20}A}=-\frac{bC}{S^2}\vec{\jmath}_0$

de donde

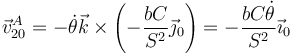
$\vec{v}^A_{20}=-\dot{\theta}\vec{k}\times\left( -\frac{bC}{S^2}\vec{\jmath}_0\right)=-\frac{bC\dot{\theta}}{S^2}\vec{\imath}_0$

Luego, la absoluta se puede hallar como suma de la relativa y la de arrastre

$\vec{v}^A_{21}=\vec{v}^A_{20}+\vec{v}^A_{01}=-\frac{bC\dot{\theta}}{S^2}\vec{\imath}_0+\frac{b\dot{\theta}}{S}\vec{\jmath}_0=-\frac{b\dot{\theta}}{S^2}\left(C\vec{\imath}_0-S\vec{\jmath}_0\right)=-\frac{b\dot{\theta}}{S^2}\vec{\imath}_1$

@@ Línea 113: / Línea 113: @@
 de donde
-<center><math>\vec{v}^A_{20}=-\dot{\theta}\vec{k}\times\left( -\frac{bC}{S^2}\vec{\jmath}_0\right)=-\frac{bC\fot{\theta}}{S^2}\vec{\imath}_0</math></center>
+<center><math>\vec{v}^A_{20}=-\dot{\theta}\vec{k}\times\left( -\frac{bC}{S^2}\vec{\jmath}_0\right)=-\frac{bC\dot{\theta}}{S^2}\vec{\imath}_0</math></center>
 Luego, la absoluta se puede hallar como suma de la relativa y la de arrastre
-<center><math>\vec{v}^A_{21}=\vec{v}^A_{20}+\vec{v}^A_{01}=-\frac{bC\fot{\theta}}{S^2}\vec{\imath}_0+\frac{b\dot{\theta}}{S}\vec{\jmath}_0=-\frac{b\dot{\theta}}{S^2}\left(C\vec{\imath}_0-S\vec{\jmath}_0\right)=-\frac{b\dot{\theta}}{S^2}\vec{\imath}_1</math></center>
+<center><math>\vec{v}^A_{21}=\vec{v}^A_{20}+\vec{v}^A_{01}=-\frac{bC\dot{\theta}}{S^2}\vec{\imath}_0+\frac{b\dot{\theta}}{S}\vec{\jmath}_0=-\frac{b\dot{\theta}}{S^2}\left(C\vec{\imath}_0-S\vec{\jmath}_0\right)=-\frac{b\dot{\theta}}{S^2}\vec{\imath}_1</math></center>

Barra apoyada en placa cuadrada (CMR)

De Laplace

Revisión de 21:24 7 dic 2020

Contenido

1 Enunciado

2 Centros instantáneos de rotación

2.1 Del movimiento {01}

2.2 Del movimiento {21}

2.3 Del movimiento {20}

3 Velocidad de A

3.1 Primer método

3.2 Segundo método

3.3 Tercer método

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES