Cinemática de dos barras articuladas (CMR)
De Laplace
(Página creada con '==Enunciado== Se tiene un sistema articulado formado por dos barras de la misma masa y la misma longitud b situadas sobre una superficie horizontal. La primera barra (“sólido…') |
|||
| Línea 19: | Línea 19: | ||
:y respecto al sistema fijo | :y respecto al sistema fijo | ||
<center><math>\omega_{31}=\omega_{32}+\omega_{21}=\dot{\theta}+\dot{\phi}</math></center> | <center><math>\omega_{31}=\omega_{32}+\omega_{21}=\dot{\theta}+\dot{\phi}</math></center> | ||
| - | |||
==Velocidades== | ==Velocidades== | ||
| + | ===De A=== | ||
| + | La velocidad de A es simplemente la de una rotación en torno a O | ||
| + | |||
| + | <center><math>\vec{v}^A_{21}=\omega_{01}\vec{k}\times\overightarrow{OA}=\dot{\phi}\vec{k}\times(b\vec{\imath}_2)=b\dot{\phi}\vec{\jmath}_2</math></center> | ||
| + | |||
| + | ===De B=== | ||
| + | La velocidad de B la obtenemos mediante el campo de velocidades | ||
| + | <center><math>\vec{v}^B_{31}=\vec{v}^A_{31}+\omega_{31}\vec{k}\times\overrightarrow{AB}=\vec{v}^A_{31}+(\dot{\phi}+\dot{\theta})\vec{k}\times(b\vec{\imath}_3</math></center> | ||
| + | |||
| + | El punto A, por ser una articulación entre “2” y “3”, tiene la misma velocidad en ambos sólidos respecto al “1” | ||
| + | |||
| + | <center><math>\vec{v}^A_{31}=\vec{v}^A_{32}+\vec{v}^A_{21}=\vec{0}+b\dot{\phi}\vec{\jmath}_2</math></center> | ||
| + | |||
| + | y, por tanto, la velocidad de B es | ||
| + | |||
| + | <center><math>\mathrm{\vec{v}^B_{31}=b\dot{\phi}\vec{\jmath}_2+b(\dot{\phi}+\dot{\theta})\vec{\jmath}_3</math></center> | ||
| + | |||
| + | Si queremos expresar esta velocidad empleando exclusivamente la base “2” simplemente desarrollamos el último vector | ||
| + | |||
| + | <center><math>\mathrm{\vec{v}^B_{31}=-b(\dot{\phi}+\dot{\theta})\mathrm{sen}(\theta)\vec{\imath}_2+b(\dot{\phi}+(\dot{\phi}+\dot{\theta})\cos(\theta))\vec{\jmath}_2</math></center> | ||
| + | |||
==Centros instantáneos de rotación== | ==Centros instantáneos de rotación== | ||
==Aceleraciones== | ==Aceleraciones== | ||
Revisión de 11:58 3 dic 2020
Contenido |
1 Enunciado
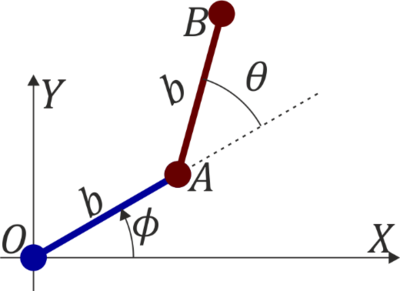
Se tiene un sistema articulado formado por dos barras de la misma masa y la misma longitud b situadas sobre una superficie horizontal. La primera barra (“sólido 2”) tiene un extremo O fijo, de forma que gira alrededor de él formando un ángulo φ(t) respecto a un sistema de ejes fijos OX1Y1. La segunda barra (“sólido 3”) está articulada en el extremo A de la primera de manera que forma un ángulo θ(t) con la prolongación del sólido 0. En función de θ, φ y sus derivadas y con ayuda de un sistema OX2Y2 ligado a la primera barra…
- Calcule la velocidad del punto de articulación A y del extremo libre B de la segunda barra respecto al sistema fijo “1”.
- Localice la posición del centro instantáneo de rotación I31 del movimiento de la segunda barra respecto a los ejes fijos.
- Halle la aceleración del extremo B y del centro G del sólido 3 respecto al sistema fijo.
2 Sistemas de referencia
Emplearemos tres sistemas de referencia:
- El sistema fijo 1, que consideramos inmóvil.
- El sistema 2, ligado a la primera varilla, con el mismo origen, y tal que el eje OX2 está alineado con ella. Cuando θ = 0, este eje es coincidente con el OX1. En este sistema, la posición del extremo A respoecto al origen es
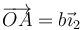
- y la velocidad angular de este sólido
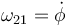
- usamos cantidades escalares porque al tratarse de un problema plano todas las velocidades angulares tienen la misma dirección (el sentido lo da el signo).
- Un sistema 3, ligado a la segunda varilla, con el eje OX3 a lo largo de ella. Cuando θ = 0, coincide con OX2. La posición del extremo B respecto a A es
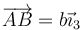
- La velocidad angular de la varilla 3 respecto a la 2 es
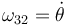
- y respecto al sistema fijo
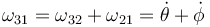
3 Velocidades
3.1 De A
La velocidad de A es simplemente la de una rotación en torno a O
3.2 De B
La velocidad de B la obtenemos mediante el campo de velocidades
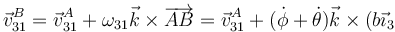
El punto A, por ser una articulación entre “2” y “3”, tiene la misma velocidad en ambos sólidos respecto al “1”
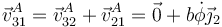
y, por tanto, la velocidad de B es
Si queremos expresar esta velocidad empleando exclusivamente la base “2” simplemente desarrollamos el último vector





