Ejemplos de puntos materiales
De Laplace
(Página creada con '= Enunciado = Analiza cuantitativamente en que situaciones de los siguientes movimientos el objeto que se mueve puede considerarse un punto material. Busca en internet los valor…') |
|||
| Línea 29: | Línea 29: | ||
</center> | </center> | ||
Este es un caso límite. La pelota es bastante más pequeña que la raqueta pero no mucho mas pequeña. Si tenemos en cuenta que el resultado del golpe depende de la forma de golpear la pelota (cortada, plana, liftada) y, sobre todo, con que punto exacto del cordaje se realiza, en este caso no se puede modelar la pelota como un punto material. | Este es un caso límite. La pelota es bastante más pequeña que la raqueta pero no mucho mas pequeña. Si tenemos en cuenta que el resultado del golpe depende de la forma de golpear la pelota (cortada, plana, liftada) y, sobre todo, con que punto exacto del cordaje se realiza, en este caso no se puede modelar la pelota como un punto material. | ||
| + | |||
| + | == Jugador de baloncesto == | ||
| + | |||
| + | Según la FIBA el tamaño de una pelota de baloncesto es de 23-24 cm. Escogemos <math>d=24\,\mathrm{cm}</math> como longitud característica del balón. | ||
| + | |||
| + | === Lanzamiento del triple === | ||
| + | En esta situación los sistema que interaccionan son la mano y la pelota. El promedio de una mano de un hombre adulto es de 189 mm, mientras que la longitud media de una mano femenina adulta es de 172 mm. Escogemos <math>L_1=180\,\mathrm{mm}</math> como tamaño característico. El cociente entre las dos longitudes es | ||
| + | <center> | ||
| + | <math> | ||
| + | \lambda = \dfrac{d}{L_1} = \dfrac{23\,\mathrm{cm}}{180\,\mathrm{mm}} | ||
| + | = | ||
| + | \dfrac{230\,\mathrm{mm}}{180\,\mathrm{mm}} \simeq 1. | ||
| + | </math> | ||
| + | </center> | ||
| + | Los tamaños son similares. Claramente la pelota no se puede modelar como un punto material en el lanzamiento. | ||
| + | |||
| + | === Llegada de la pelota a la canasta === | ||
| + | La distancia de la línea de tres puntos a la canasta es de 6.75 m. El cociente ahora es | ||
| + | <center> | ||
| + | <math> | ||
| + | \lambda = \dfrac{d}{L_2} = \dfrac{24\,\mathrm{cm}}{6.75\,\mathrm{m}} | ||
| + | = | ||
| + | \dfrac{0.24\,\mathrm{m}}{6.75\,\mathrm{m}} \simeq 0.04. | ||
| + | </math> | ||
| + | </center> | ||
| + | Al ser muy pequeño el movimiento de la pelota se puede modelar como un punto material desde el punto de vista del jugador. | ||
| + | |||
| + | === Relación entre la pelota y la canasta === | ||
| + | El diámetro de una canasta de baloncesto debe estar entre 450 y 459 mm. Si escogemos <math>L_3=460\,\mathrm{mm}</math>, el cociente relevante es | ||
| + | <center> | ||
| + | <math> | ||
| + | \lambda = | ||
| + | \dfrac{d}{L_3} = \dfrac{24\,\mathrm{cm}}{460\,\mathrm{mm}} | ||
| + | = | ||
| + | \dfrac{240\,\mathrm{cm}}{460\,\mathrm{mm}} | ||
| + | \simeq 0.5. | ||
| + | </math> | ||
| + | </center> | ||
| + | Son de tamaños similares, por lo que ninguno de los dos objetos se puede modelar como un punto material en esta interacción. | ||
Revisión de 01:20 13 feb 2006
Contenido |
1 Enunciado
Analiza cuantitativamente en que situaciones de los siguientes movimientos el objeto que se mueve puede considerarse un punto material. Busca en internet los valores de las longitudes que necesites.
- Una jugadora de tenis recibe un saque.
- Un jugador de baloncesto lanza un triple.
- La Luna vista desde el Apollo XI.
- El cometa Halley visto desde el Sol.
2 Solución
2.1 Jugadora de tenis
En esta situación el objeto que queremos modelar como un punto material es la pelota de tenis. Podemos escoger su diámetro como longitud que la caracterice. Según la Federación Internacional de Tenis la pelota debe ser mayor de 6.54 cm y menor de 6.86 cm. Como el objetivo es un cálculo de orden de magnitud escogemos 
para caracterizar la pelota.
2.1.1 Recepción del saque
Cuando la jugadora va a recibir el saque la distancia entre ella y la pelota es la longitud de la pista. El valor oficial es 23.77 m. Escogemos el valor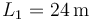 
para caracterizarla. Entonces, el cociente entre las dos longitudes es
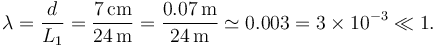
Como este cociente es muy pequeño, concluimos que en la situación de recepción del saque la jugadora puede modelar la pelota como una partícula material.
2.1.2 Golpeo del resto
En este caso los sistemas que interaccionan son la pelota y la raqueta. La longitud estándar de las raquetas de tenis es de 68.5 cm. Escogemos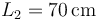 
como longitud característica de la raqueta. El cociente ahora es
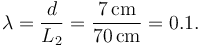
Este es un caso límite. La pelota es bastante más pequeña que la raqueta pero no mucho mas pequeña. Si tenemos en cuenta que el resultado del golpe depende de la forma de golpear la pelota (cortada, plana, liftada) y, sobre todo, con que punto exacto del cordaje se realiza, en este caso no se puede modelar la pelota como un punto material.
2.2 Jugador de baloncesto
Según la FIBA el tamaño de una pelota de baloncesto es de 23-24 cm. Escogemos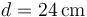 
como longitud característica del balón.
2.2.1 Lanzamiento del triple
En esta situación los sistema que interaccionan son la mano y la pelota. El promedio de una mano de un hombre adulto es de 189 mm, mientras que la longitud media de una mano femenina adulta es de 172 mm. Escogemos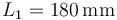 
como tamaño característico. El cociente entre las dos longitudes es
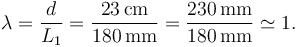
Los tamaños son similares. Claramente la pelota no se puede modelar como un punto material en el lanzamiento.
2.2.2 Llegada de la pelota a la canasta
La distancia de la línea de tres puntos a la canasta es de 6.75 m. El cociente ahora es
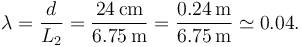
Al ser muy pequeño el movimiento de la pelota se puede modelar como un punto material desde el punto de vista del jugador.
2.2.3 Relación entre la pelota y la canasta
El diámetro de una canasta de baloncesto debe estar entre 450 y 459 mm. Si escogemos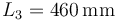 
, el cociente relevante es
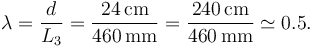
Son de tamaños similares, por lo que ninguno de los dos objetos se puede modelar como un punto material en esta interacción.
