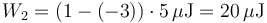Sistema de tres esferas
De Laplace
(Página creada con '==Enunciado== Un sistema de conductores está formado por tres esferas metálicas idénticas de radio b, situadas en los vértices de un triángulo equilátero de lado a ((a>2b)…') |
(→Nueva energía) |
||
| (2 ediciones intermedias no se muestran.) | |||
| Línea 31: | Línea 31: | ||
<center><math>Q_1 = C_a(V_1-V_2)+C_a(V_1-V_3)+C_b (V_1-0)\,</math></center> | <center><math>Q_1 = C_a(V_1-V_2)+C_a(V_1-V_3)+C_b (V_1-0)\,</math></center> | ||
| - | Sustituimos | + | Sustituimos y, dado que <math>V_2=V_3=0</math>, queda |
<center><math>8\,\mathrm{nC}=(2C_a+C_b)(10\,\mathrm{kV})\qquad\Rightarrow\qquad 2C_a+C_b=0.8\,\mathrm{pF}</math></center> | <center><math>8\,\mathrm{nC}=(2C_a+C_b)(10\,\mathrm{kV})\qquad\Rightarrow\qquad 2C_a+C_b=0.8\,\mathrm{pF}</math></center> | ||
| Línea 39: | Línea 39: | ||
<center><math>Q_2 = C_a(V_2-V_1)+C_a(V_2-V_3)+C_b (V_2-0)\,</math></center> | <center><math>Q_2 = C_a(V_2-V_1)+C_a(V_2-V_3)+C_b (V_2-0)\,</math></center> | ||
| - | Sustituimos | + | Sustituimos |
| - | <center><math>-3\,\mathrm{nC}= | + | <center><math>-3\,\mathrm{nC}=C_a(-10\,\mathrm{kV})</math></center> |
De aquí obtenemos | De aquí obtenemos | ||
| Línea 67: | Línea 67: | ||
==Nueva energía== | ==Nueva energía== | ||
| - | Una vez que tenemos las cargas y los | + | Una vez que tenemos las cargas y los potenciales, hallamos la nueva energía, |
<center><math>U'_\mathrm{e}=\frac{1}{2}(6.5\cdot 10+1\cdot 5+(-4.5)\cdot 0)\,\mu\mathrm{J}=35\,\mu\mathrm{J}</math></center> | <center><math>U'_\mathrm{e}=\frac{1}{2}(6.5\cdot 10+1\cdot 5+(-4.5)\cdot 0)\,\mu\mathrm{J}=35\,\mu\mathrm{J}</math></center> | ||
última version al 19:08 13 may 2020
Contenido |
1 Enunciado
Un sistema de conductores está formado por tres esferas metálicas idénticas de radio b, situadas en los vértices de un triángulo equilátero de lado a ((a>2b). No hay más conductores ni cargas en el sistema.
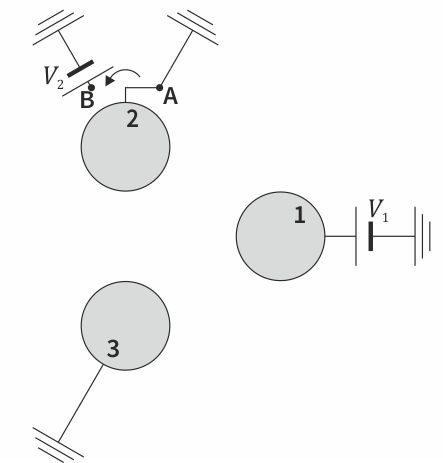
Se encuentra experimentalmente que cuando la esfera “1” se encuentra a 10kV y la “2” y la “3” a tierra, la carga de la propia esfera “1” es de +8nC, mientras que la de la “2” es de −3nC.
Nota: Para resolver este problema no se necesita usar la capacidad de una esfera
- Calcule la energía eléctrica almacenada en el sistema.
- Se puede construir un circuito equivalente a este sistema de conductores. Está formado por seis condensadores: tres iguales que conectan cada par de esferas y otros tres también iguales, cada uno conectando una esfera al infinito. Dibuje el circuito y calcule las capacidades de estos condensadores.
Suponga que, sin tocar las esferas 1 y 3, se pasa el interruptor de la esfera 2 a la posición B, de manera que su voltaje pasa a ser de 5kV. Una vez que se llega al equilibrio:
- ¿Cuál es la nueva carga de cada esfera?
- ¿Cuál es la nueva energía almacenada?
- ¿Qué trabajo realiza en el proceso el generador conectado a la esfera 1 y el conectado a la esfera 2?
2 Energía inicial
Para hallar la energía de un sistema de conductores aplicamos que
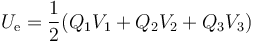
En este caso, no nos dan la carga del conductor “3” (aunque por la simetría del sistema, debe ser igual a la de la esfera “2”), pero da igual porque su potencial es 0. Por tanto, queda
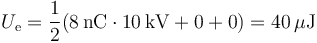
3 Circuito equivalente
De acuerdo con lo visto en teoría, y tal como se dice en el enunciado, cada conductor equivale a un nodo. Hay un condensador entre cada dos nodos (que tendrán los tres la misma capacidad Ca, por la simetría del sistema) y otro entre cada nodo y tierra, representando las líneas de campo que van al infinito (y estos tres tendrán la misma capacidad Cb). A eso se añaden las fuentes oportunas. Quedaría como sigue:
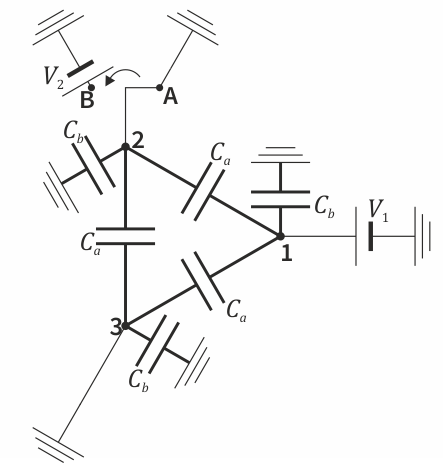
Para hallar las capacidades de estos condensadores, aplicamos que nos dan cargas y potenciales. La carga de un conductor equivale a la de todas las placas conectadas al nodo correspondiente. Para el conductor 1
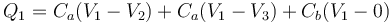
Sustituimos y, dado que V2 = V3 = 0, queda

Para el conductor 2
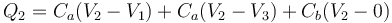
Sustituimos
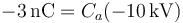
De aquí obtenemos
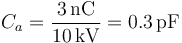
y, sustituyendo esto en la ecuación para "1", la otra capacidad
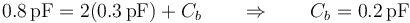
4 Nuevas cargas
Tras la conexión, el conductor 2, pasa a estar a 5kV.
La nueva carga del conductor 1 es
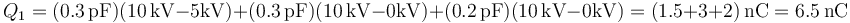
La del 2
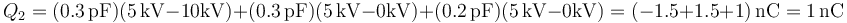
y la del 3
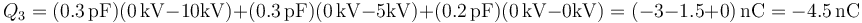
5 Nueva energía
Una vez que tenemos las cargas y los potenciales, hallamos la nueva energía,
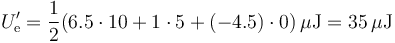
6 Trabajo de los generadores
El trabajo de cada generador es igual a
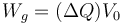
lo que da, para el generador conectado a la esfera 1
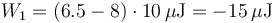
y para el conectado a la esfera 2