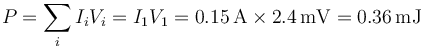Circuito en forma de H (GIOI)
De Laplace
(→Intensidades de corriente) |
|||
| Línea 60: | Línea 60: | ||
Con esto tenemos la corriente que entra por 1. | Con esto tenemos la corriente que entra por 1. | ||
| - | <center><math>I_1=\frac{V_0}{R_\mathrm{eq}}=\frac{2.4\,\mathrm{mV}}{15\,\mathrm{m}\Omega}= | + | <center><math>I_1=\frac{V_0}{R_\mathrm{eq}}=\frac{2.4\,\mathrm{mV}}{15\,\mathrm{m}\Omega}=0.16\,\mathrm{A}</math></center> |
| - | Esta corriente se separa en dos ramas de la misma resistencia <math>R_0</math>, con lo que por cada una se van | + | Esta corriente se separa en dos ramas de la misma resistencia <math>R_0</math>, con lo que por cada una se van 0.08 A. Por tanto, la corriente que entra por “3”, que en realidad sale, vale |
| - | <center><math>I_3=- | + | <center><math>I_3=-0.08\,\mathrm{A}</math></center> |
| - | La que va por la otra rama se bifurca de nuevo en dos ramas iguales, por lo que por cada una se van | + | La que va por la otra rama se bifurca de nuevo en dos ramas iguales, por lo que por cada una se van 0.04 A. Por tanto |
| - | <center><math>I_2=I_4=- | + | <center><math>I_2=I_4=-0.04\,\mathrm{A}</math></center> |
===Voltajes=== | ===Voltajes=== | ||
| - | El voltaje del nodo B lo sacamos de que por 1 entra una corriente de | + | El voltaje del nodo B lo sacamos de que por 1 entra una corriente de 0.16 A, por lo que |
| - | <center><math>I_1=\frac{V_1-V_B}{R_0}\qquad\Rightarrow\qquad | + | <center><math>I_1=\frac{V_1-V_B}{R_0}\qquad\Rightarrow\qquad 0.16\,\mathrm{A}=\frac{2.4\,\mathrm{mV}-V_B}{10\,\mathrm{m}\Omega} \qquad\Rightarrow\qquad V_B=0.8\,\mathrm{mV}</math></center> |
| - | y la de C de manera similar, sabiendo que por la rama BC van | + | y la de C de manera similar, sabiendo que por la rama BC van 0.08 A |
| - | <center><math> | + | <center><math>0.08\,\mathrm{A}=\frac{0.8\,\mathrm{mV}-V_C}{5\,\mathrm{m}\Omega}\qquad\Rightarrow\qquad V_C=0.4\,\mathrm{mV}</math></center> |
A estos mismso resultados se puede llegar de diferentes formas. | A estos mismso resultados se puede llegar de diferentes formas. | ||
| Línea 83: | Línea 83: | ||
La potencia consumida en un sistema con varios terminales es | La potencia consumida en un sistema con varios terminales es | ||
| - | <center><math>P=\sum_i I_i V_i = I_1 V_1 = | + | <center><math>P=\sum_i I_i V_i = I_1 V_1 = 0.16\,\mathrm{A}\times 2.4\,\mathrm{mV}= 0.384\,\mathrm{mJ}</math></center> |
==Con el interruptor abierto== | ==Con el interruptor abierto== | ||
===Intensidades de corriente=== | ===Intensidades de corriente=== | ||
| Línea 107: | Línea 107: | ||
y por tanto la corriente que entra por 1 es ahora | y por tanto la corriente que entra por 1 es ahora | ||
| - | <center><math>I_1=\frac{V_0}{R_\mathrm{eq}}=\frac{2.4\,\mathrm{mV}}{16\,\mathrm{m}\Omega}= | + | <center><math>I_1=\frac{V_0}{R_\mathrm{eq}}=\frac{2.4\,\mathrm{mV}}{16\,\mathrm{m}\Omega}=0.15\,\mathrm{A}</math></center> |
Esta corriente se bifurca en dos ramas, pero ahora las resistencias son diferentes, por lo que las intensidades no son iguales. Para obtenerlas podemos emplear las leyes de Kirchhoff | Esta corriente se bifurca en dos ramas, pero ahora las resistencias son diferentes, por lo que las intensidades no son iguales. Para obtenerlas podemos emplear las leyes de Kirchhoff | ||
| - | <center><math>- | + | <center><math>-0.15=I_3+I_4\qquad\qquad 10I_3=15I_4 \qquad\Rightarrow\qquad I_3=-0.09\,\mathrm{A}\qquad\qquad I_4=-0.06\,\mathrm{A}</math></center> |
(el signo negativo viene de que la corrientes salen por 3 y 4, no entran). | (el signo negativo viene de que la corrientes salen por 3 y 4, no entran). | ||
| Línea 117: | Línea 117: | ||
Resumiendo | Resumiendo | ||
| - | <center><math>I_1= | + | <center><math>I_1=0.15\,\mathrm{A}\qquad\qquad I_2=0\qquad \qquad I_3=-0.09\,\mathrm{A}\qquad\qquad I_4=-0.06\,\mathrm{A}</math></center> |
===Voltajes=== | ===Voltajes=== | ||
| Línea 126: | Línea 126: | ||
La potencia consumida es ahora | La potencia consumida es ahora | ||
| - | <center><math>P=\sum_i I_i V_i = I_1 V_1 = | + | <center><math>P=\sum_i I_i V_i = I_1 V_1 = 0.15\,\mathrm{A}\times 2.4\,\mathrm{mV}= 0.36\,\mathrm{mJ}</math></center> |
última version al 13:56 20 abr 2020
Contenido |
1 Enunciado
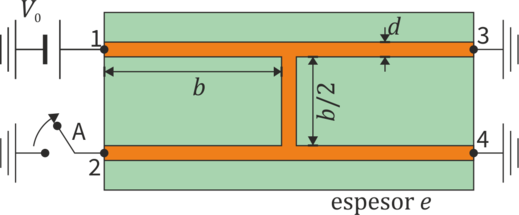
Un circuito integrado está constituido por una pista de cobre (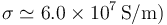 de espesor e=0.1 mm montada sobre un dieléctrico. La pista tiene en todos sus tramos un ancho d = 1.0 mm. La pista tiene forma de H, en la que cada tramo mide b = 6.0 cm, salvo el travesaño central, que mide 3cm.
Supongamos en primer lugar, que tres de las patas están a tierra (el interruptor A está cerrado) y la cuarta conectada a un voltaje
de espesor e=0.1 mm montada sobre un dieléctrico. La pista tiene en todos sus tramos un ancho d = 1.0 mm. La pista tiene forma de H, en la que cada tramo mide b = 6.0 cm, salvo el travesaño central, que mide 3cm.
Supongamos en primer lugar, que tres de las patas están a tierra (el interruptor A está cerrado) y la cuarta conectada a un voltaje 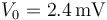 .
.
- Halle la intensidad de corriente que entra o sale por cada pata.
- Halle el voltaje al que se encuentran los dos nodos intermedios, donde se unen los diferentes tramos.
- Calcule la potencia que se está disipando en el sistema por efecto Joule.
Supongamos ahora que, en la situación anterior, se abre el interruptor A, dejando la pata 2 en circuito abierto. Responda a las mismas preguntas:
- Halle la intensidad de corriente que entra o sale por cada pata.
- Halle el voltaje al que se encuentran los dos nodos intermedios.
- Calcule la potencia que se está disipando en el sistema por efecto Joule.
Puede suponerse cada tramo como un conductor filiforme.
2 Con el interruptor cerrado
2.1 Intensidades de corriente
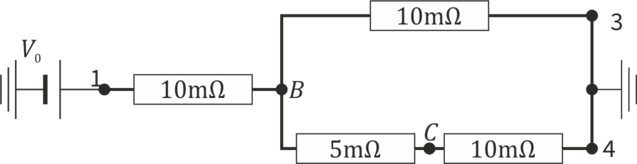
Construimos un circuito equivalente, sustituyendo cada tramo por una resistencia. Etiquetamos cada una por el nodo que tiene más próximo y R5 es la del brazo central. Los nodos B y C son las esquinas donde se unen los tramos.
Para los tramos de 6cm la resistencia vale
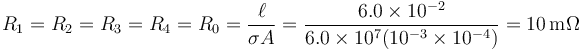
mientras que la del tramo central es la mitad, por serlo su longitud
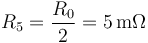
En principio, estas resistencias están dispuestas según la misma H.
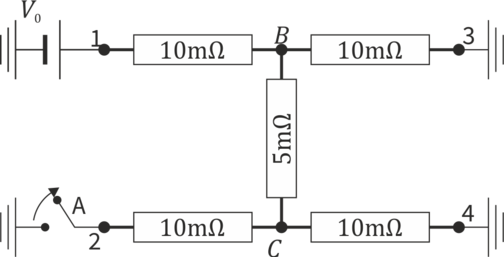
Sin embargo, dado que tres de sus patas están a tierra y solo una a un cierto voltaje, puede simplificarse mediante asociaciones.

Podemos ver que tenemos una resistencia R1 que sale de “1” y en el punto B se bifurca en 2 ramas en paralelo, una de las cuales vuelve a bifurcarse en el punto C. La resistencia equivalente a la que va de C a 2 y la que va de B a 4 vale


Esta asociación está en serie con la resistencia del tramo central

y esta en paralelo con la que va a 3.
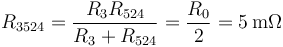

Por tanto la resistencia equivalente a todo el conjunto, visto desde “1” es
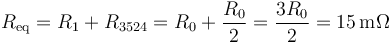

Con esto tenemos la corriente que entra por 1.
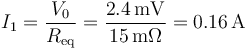
Esta corriente se separa en dos ramas de la misma resistencia R0, con lo que por cada una se van 0.08 A. Por tanto, la corriente que entra por “3”, que en realidad sale, vale
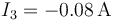
La que va por la otra rama se bifurca de nuevo en dos ramas iguales, por lo que por cada una se van 0.04 A. Por tanto
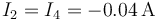
2.2 Voltajes
El voltaje del nodo B lo sacamos de que por 1 entra una corriente de 0.16 A, por lo que

y la de C de manera similar, sabiendo que por la rama BC van 0.08 A
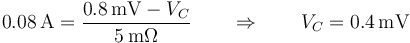
A estos mismso resultados se puede llegar de diferentes formas.
2.3 Potencia
La potencia consumida en un sistema con varios terminales es

3 Con el interruptor abierto
3.1 Intensidades de corriente
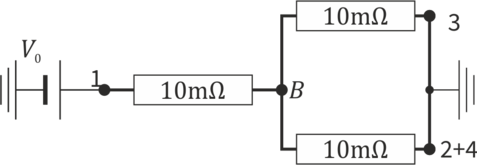
Cuando se abre el interruptor, la rama 2 queda desconectada y por ella ni entra ni sale corriente. Por tanto, desde el punto de vista del circuito, es como si no estuviera.

Esto hace que cambie la resistencia equivalente del circuito, que vale ahora
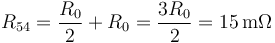





y por tanto la corriente que entra por 1 es ahora

Esta corriente se bifurca en dos ramas, pero ahora las resistencias son diferentes, por lo que las intensidades no son iguales. Para obtenerlas podemos emplear las leyes de Kirchhoff

(el signo negativo viene de que la corrientes salen por 3 y 4, no entran).
Resumiendo
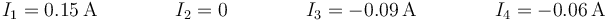
3.2 Voltajes
Operamos igual que antes y resulta

3.3 Potencia
La potencia consumida es ahora