Conexión de dos esferas alejadas
De Laplace
(→Empleando un circuito equivalente) |
(→Densidad de carga y campo) |
||
| (6 ediciones intermedias no se muestran.) | |||
| Línea 5: | Línea 5: | ||
# ¿En cual de las dos esferas es mayor la densidad de carga? ¿Y el campo eléctrico en la superficie? | # ¿En cual de las dos esferas es mayor la densidad de carga? ¿Y el campo eléctrico en la superficie? | ||
| - | <center>[[Imagen:dosesferashilo.png]]</center> | + | <center>[[Imagen:dosesferashilo-02.png]]</center> |
==Carga en cada esfera== | ==Carga en cada esfera== | ||
| Línea 11: | Línea 11: | ||
Al estar muy alejadas, las dos esferas se comportan como conductores independientes, salvo por el hecho de que están conectadas por un hilo. Este hilo, al ser ideal, no añade capacidad ni carga al sistema, pero garantiza que ambas esferas estén al mismo potencial, ya que las cargas pueden moverse de una esfera a la otra. | Al estar muy alejadas, las dos esferas se comportan como conductores independientes, salvo por el hecho de que están conectadas por un hilo. Este hilo, al ser ideal, no añade capacidad ni carga al sistema, pero garantiza que ambas esferas estén al mismo potencial, ya que las cargas pueden moverse de una esfera a la otra. | ||
| - | El [[ | + | El [[Esfera conductora en equilibrio electrostático|potencial en cada una de las esferas]] será, en función de su carga |
<center> | <center> | ||
| - | <math>V_1 = \frac{Q_1}{4\pi\varepsilon_0 a}</math>{{qquad}}{{qquad}}<math>V_2 = \frac{ | + | <math>V_1 = \frac{Q_1}{4\pi\varepsilon_0 a}</math>{{qquad}}{{qquad}}<math>V_2 = \frac{Q_2}{4\pi\varepsilon_0 b}</math></center> |
Si las dos esferas están al mismo potencial nos queda | Si las dos esferas están al mismo potencial nos queda | ||
| Línea 20: | Línea 20: | ||
<math>V_1 = V_2\,</math>{{tose}}<math>\frac{Q_1}{a}=\frac{Q_2}{b}</math></center> | <math>V_1 = V_2\,</math>{{tose}}<math>\frac{Q_1}{a}=\frac{Q_2}{b}</math></center> | ||
| - | lo que nos dice que la carga será mayor en la esfera más grande, en una cantidad proporcional a su radio (doble radio, doble carga). | + | lo que nos dice que la carga será mayor en la esfera más grande, en una cantidad proporcional no a su área sino a su radio (doble radio, doble carga). |
Como además la carga total es <math>Q</math>, tenemos el sistema de ecuaciones | Como además la carga total es <math>Q</math>, tenemos el sistema de ecuaciones | ||
| Línea 49: | Línea 49: | ||
<center><math>V = \frac{Q_0}{C_\mathrm{eq}}= \frac{Q_0}{4\pi\varepsilon_0(a+b)}</math></center> | <center><math>V = \frac{Q_0}{C_\mathrm{eq}}= \frac{Q_0}{4\pi\varepsilon_0(a+b)}</math></center> | ||
| - | Una vez que tenemos el potencial, podemos hallar la carga en cada una de las esferas, que | + | Una vez que tenemos el potencial, podemos hallar la carga en cada una de las esferas, que corresponden a las placas positivas de los condensadores. |
<center><math>Q_1 = C_1 V = \frac{C_1 Q_0}{C_\mathrm{eq}} = \frac{Q_0 a}{a+b}</math>{{qquad}}{{qquad}}<math>Q_2 = C_2 V = \frac{C_2 Q_0}{C_\mathrm{eq}} = \frac{Q_0 b}{a+b}</math></center> | <center><math>Q_1 = C_1 V = \frac{C_1 Q_0}{C_\mathrm{eq}} = \frac{Q_0 a}{a+b}</math>{{qquad}}{{qquad}}<math>Q_2 = C_2 V = \frac{C_2 Q_0}{C_\mathrm{eq}} = \frac{Q_0 b}{a+b}</math></center> | ||
| Línea 56: | Línea 56: | ||
Tal como se ve en el caso de una sola esfera, la densidad de carga en la superficie de una esfera cuando no hay más cargas o conductores influyendo sobre ella, es uniforme e igual a | Tal como se ve en el caso de una sola esfera, la densidad de carga en la superficie de una esfera cuando no hay más cargas o conductores influyendo sobre ella, es uniforme e igual a | ||
| - | <center><math>\sigma_s=\frac{ | + | <center><math>\sigma_s=\frac{Q}{4\pi R^2}</math></center> |
| - | lo cual quiere decir que las densidades de carga en las dos esferas | + | lo cual quiere decir que las densidades de carga en las dos esferas valen |
| - | <center><math>\sigma_1=\frac{ | + | <center><math>\sigma_1=\frac{Q_1}{4\pi a^2}</math>{{qquad}}{{qquad}}<math>\sigma_2=\frac{Q_2}{4\pi b^2}</math></center> |
| - | + | ||
| - | + | ||
En términos de la carga total | En términos de la carga total | ||
<center><math>\sigma_1=\frac{Q_0}{4\pi a(a+b)}</math>{{qquad}}{{qquad}}<math>\sigma_2=\frac{Q_0}{4\pi b(a+b)}</math></center> | <center><math>\sigma_1=\frac{Q_0}{4\pi a(a+b)}</math>{{qquad}}{{qquad}}<math>\sigma_2=\frac{Q_0}{4\pi b(a+b)}</math></center> | ||
| + | |||
| + | Observemos que esto implica que | ||
| + | |||
| + | <center><math>\frac{Q_2}{Q_1}=\frac{b}{a}\geq 1 \qquad\qquad \frac{\sigma_2}{\sigma_1}=\frac{a}{b}\leq 1</math></center> | ||
| + | |||
| + | esto es, que cuanto más pequeña sea la esfera, mayor es su densidad de carga (aunque la carga total sea menor). | ||
En cuanto al campo en la superficie, puesto que es proporcional a la carga superficial, también será más intenso en la esfera de menor radio | En cuanto al campo en la superficie, puesto que es proporcional a la carga superficial, también será más intenso en la esfera de menor radio | ||
| Línea 74: | Línea 78: | ||
Esta es una aplicación de un principio más general, conocido como ''efecto punta'': ''el campo eléctrico en la superficie de un conductor es más intenso donde el radio de curvatura es más pequeño''. Este principio se encuentra, por ejemplo, en la base del funcionamiento de los pararrayos. | Esta es una aplicación de un principio más general, conocido como ''efecto punta'': ''el campo eléctrico en la superficie de un conductor es más intenso donde el radio de curvatura es más pequeño''. Este principio se encuentra, por ejemplo, en la base del funcionamiento de los pararrayos. | ||
| + | [[Categoría:Problemas de electrostática en medios materiales (GIOI)]] | ||
[[Categoría:Problemas de electrostática en medios materiales (GIE)]] | [[Categoría:Problemas de electrostática en medios materiales (GIE)]] | ||
última version al 21:10 15 mar 2020
Contenido |
1 Enunciado
Se tiene un conductor formado por dos esferas de radios a y b (a < b), muy alejadas entre sí (de forma que la influencia de una sobre la otra es despreciable), pero unidas por un cable conductor ideal. El conductor almacena una carga Q0.
- ¿Cuánta carga se va a cada esfera? ¿En cuál de las dos es mayor la carga almacenada?
- ¿En cual de las dos esferas es mayor la densidad de carga? ¿Y el campo eléctrico en la superficie?

2 Carga en cada esfera
2.1 Cálculo directo
Al estar muy alejadas, las dos esferas se comportan como conductores independientes, salvo por el hecho de que están conectadas por un hilo. Este hilo, al ser ideal, no añade capacidad ni carga al sistema, pero garantiza que ambas esferas estén al mismo potencial, ya que las cargas pueden moverse de una esfera a la otra.
El potencial en cada una de las esferas será, en función de su carga
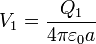
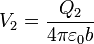
Si las dos esferas están al mismo potencial nos queda
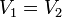

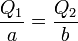
lo que nos dice que la carga será mayor en la esfera más grande, en una cantidad proporcional no a su área sino a su radio (doble radio, doble carga).
Como además la carga total es Q, tenemos el sistema de ecuaciones
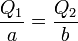
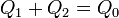
con solución

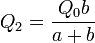
El potencial en el conjunto es
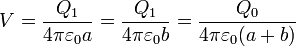
2.2 Empleando un circuito equivalente
La carga en cada esfera también es fácil de calcular empleando un circuito equivalente. Tal como se demuestra en otro problema, cada esfera forma con el infinito un condensador de capacidad

La esfera de mayor radio tiene mayor capacidad, proporcional a él.
Al unirlos con el hilo, estos dos condensadores se conectan en paralelo (ya que dos de las placas están unidas por el hilo y las otras dos están también al mismo potencial, el de tierra). La capacidad de la asociación será
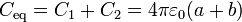
y, por tanto, el potencial de las placas cargadas (que son las esferas) es
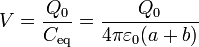
Una vez que tenemos el potencial, podemos hallar la carga en cada una de las esferas, que corresponden a las placas positivas de los condensadores.

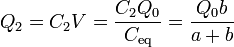
3 Densidad de carga y campo
Tal como se ve en el caso de una sola esfera, la densidad de carga en la superficie de una esfera cuando no hay más cargas o conductores influyendo sobre ella, es uniforme e igual a
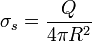
lo cual quiere decir que las densidades de carga en las dos esferas valen
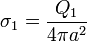
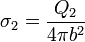
En términos de la carga total
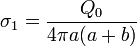
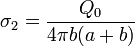
Observemos que esto implica que

esto es, que cuanto más pequeña sea la esfera, mayor es su densidad de carga (aunque la carga total sea menor).
En cuanto al campo en la superficie, puesto que es proporcional a la carga superficial, también será más intenso en la esfera de menor radio
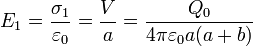
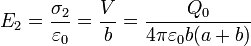
Esta es una aplicación de un principio más general, conocido como efecto punta: el campo eléctrico en la superficie de un conductor es más intenso donde el radio de curvatura es más pequeño. Este principio se encuentra, por ejemplo, en la base del funcionamiento de los pararrayos.





