Modelo de atmósfera isoterma
De Laplace
(Nueva página: ==Enunciado== Suponiendo que la densidad del aire en la atmósfera es proporcional a la presión, demuestre que la variación de la presión atmosférica con la altura es <math>P(y) =...) |
(→Introducción) |
||
| Línea 4: | Línea 4: | ||
==Solución== | ==Solución== | ||
===Introducción=== | ===Introducción=== | ||
| + | Antes de resolver el problema, es conveniente aclarar la razón de la palabra "isoterma" del título. Puede parecer incongruente, dado que en el enunciado del problema no se hace mención alguna a la temperatura. | ||
| + | |||
| + | La causa es la frase “Suponiendo que la densidad del aire en la atmósfera es proporcional a la presión”. Esta suposición sólo es razonablemente cierta en el caso de que la temperatura no dependa de la altura. | ||
| + | |||
| + | Si la temperatura es variable, la proporcionalidad ya no se verifica. Para entenderlo, observamos que el aire se comporta aproximadamente como un gas ideal. Para un gas ideal, se cumple la ecuación de estado | ||
| + | |||
| + | <center><math>pV = n R T\,</math></center> | ||
| + | |||
| + | La cantidad n es el número de moles, que será igual a la masa total del gas que tengamos, dividida por su peso molecular, esto es | ||
| + | |||
| + | <center><math>p V = \frac{m}{P_m}RT</math> {{tose}}<math>p = \frac{RT}{P_m}\,\frac{m}{V}=\frac{RT}{P_m}\rho</math></center> | ||
| + | |||
| + | Si la temperatura del gas es la misma en todos los puntos, la presión es proporcional a la densidad, pero si varía, habrá que tenerlo en cuenta. | ||
| + | |||
| + | Para evitar usar el peso molecular, que para el aire es simplemente un promedio (pues se trata de una mezcla de gases), podemos escribir la ecuación anterior como | ||
| + | |||
| + | <center><math>\frac{\rho T}{p}= \frac{\rho_0 T_0}{p_0}=\frac{P_m}{R}=\mathrm{cte}</math></center> | ||
| + | |||
| + | y de aquí | ||
| + | |||
| + | <center><math>\rho = \rho_0\left(\frac(T}{T_0}\right)\left(\frac(p}{p_0}\right)</math></center> | ||
| + | |||
| + | si la temperatura es la misma en todos los puntos | ||
| + | |||
| + | <center><math>\rho = \frac{\rho_0}{p_0}p</math></center> | ||
| + | |||
| + | Esta es la hipótesis que haremos en el siguiente apartado. Más adelante veremos como queda si suponemos un perfil que varía linealmente con la altura. | ||
| + | |||
===Solución isoterma=== | ===Solución isoterma=== | ||
===Solución para un perfil de temperaturas=== | ===Solución para un perfil de temperaturas=== | ||
[[Categoría:Problemas de introducción a la mecánica de fluidos]] | [[Categoría:Problemas de introducción a la mecánica de fluidos]] | ||
Revisión de 19:16 13 mar 2009
Contenido |
1 Enunciado
Suponiendo que la densidad del aire en la atmósfera es proporcional a la presión, demuestre que la variación de la presión atmosférica con la altura es P(y) = P0e − y, siendo g la aceleración de la gravedad y α = ρ0g / P0, con ρ0 y P0 la densidad del aire y la presión atmosférica a nivel del mar (y = 0).
2 Solución
2.1 Introducción
Antes de resolver el problema, es conveniente aclarar la razón de la palabra "isoterma" del título. Puede parecer incongruente, dado que en el enunciado del problema no se hace mención alguna a la temperatura.
La causa es la frase “Suponiendo que la densidad del aire en la atmósfera es proporcional a la presión”. Esta suposición sólo es razonablemente cierta en el caso de que la temperatura no dependa de la altura.
Si la temperatura es variable, la proporcionalidad ya no se verifica. Para entenderlo, observamos que el aire se comporta aproximadamente como un gas ideal. Para un gas ideal, se cumple la ecuación de estado
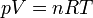
La cantidad n es el número de moles, que será igual a la masa total del gas que tengamos, dividida por su peso molecular, esto es
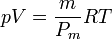

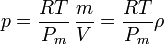
Si la temperatura del gas es la misma en todos los puntos, la presión es proporcional a la densidad, pero si varía, habrá que tenerlo en cuenta.
Para evitar usar el peso molecular, que para el aire es simplemente un promedio (pues se trata de una mezcla de gases), podemos escribir la ecuación anterior como
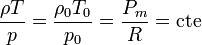
y de aquí
si la temperatura es la misma en todos los puntos

Esta es la hipótesis que haremos en el siguiente apartado. Más adelante veremos como queda si suponemos un perfil que varía linealmente con la altura.





