Examen parcial CMR 19-20

De Laplace

(Diferencias entre revisiones)

Revisión de 12:32 7 feb 2020

Contenido

1 Rotor de una sola masa
2 Momento de inercia de un cilindro
3 Disco arrastrado por una barra
4 Percusión sobre cuerpo redondo
- 4.1 Pregunta 1
- 4.2 Pregunta 2
5 Número de grados de libertad
6 Movimiento instantáneo de un sólido
7 Desplazamientos virtuales
8 Sistema de poleas
- 8.1 Pregunta 1
- 8.2 Pregunta 2

1 Rotor de una sola masa

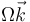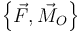Se tiene un rotor formado por una masa m unida por una varilla rígida, sin masa, a un punto O, alrededor del cual la varilla gira con velocidad angular constante $\Omega\vec{k}$ . La varilla forma un ángulo de 45° con la dirección del eje de giro. Para mantener la rotación constante, en O es necesario aplicar un sistema de fuerzas que se reduce a $\left\{\vec{F},\vec{M}_O\right\}$ .

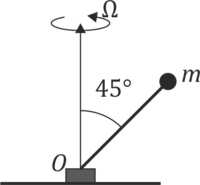
Este sistema es equivalente a…

A un sistema nulo.
B una fuerza única.
C un par de fuerzas.
D un tornillo.

Solución

La respuesta correcta es la B.

Siempre que tengamos un sistema formado por una sola partícula, el sistema de fuerzas que actúa sobre ella se podrá reducir a una fuerza única (o un sistema nulo), ya que para una única partícula basta aplicar una fuerza sobre ella para moverla.

Se puede demostrar a partir del teorema de la cantidad de movimiento y el del momento cinético. Consideramos un sistema de referencia $O X 2 Y 2 Z 2$ que gira con la velocidad 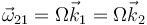$\vec{\omega}_{21}=\Omega\vec{k}_1=\Omega\vec{k}_2$ . En este sistema la posición de la partícula es

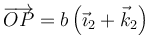
$\overrightarrow{OP}=b\left(\vec{\imath}_2+\vec{k}_2\right)$

y su velocidad

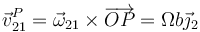
$\vec{v}^P_{21}=\vec{\omega}_{21}\times\overrightarrow{OP}=\Omega b\vec{\jmath}_2$

siendo la cantidad de movimiento y el momento cinético

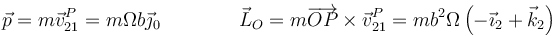
$\vec{p}=m\vec{v}^P_{21}=m\Omega b\vec{\jmath}_0\qquad\qquad\vec{L}_O=m\overrightarrow{OP}\times\vec{v}^P_{21}=mb^2\Omega\left(-\vec{\imath}_2+\vec{k}_2\right)$

El teorema de la cantidad de movimiento nos da la fuerza

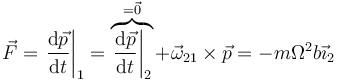
$\vec{F}=\left.\frac{\mathrm{d}\vec{p}}{\mathrm{d}t}\right|_1=\overbrace{\left.\frac{\mathrm{d}\vec{p}}{\mathrm{d}t}\right|_2}^{=\vec{0}}+\vec{\omega}_{21}\times\vec{p}=-m\Omega^2b\vec{\imath}_2$

Se puede llegar a este resultado simplemente observando que P describe un movimiento circular uniforme alrededor del eje OZ.

Por el teorema del momento cinético tenemos

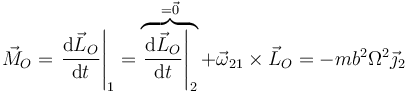
$\vec{M}_O=\left.\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}\right|_1=\overbrace{\left.\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}\right|_2}^{=\vec{0}}+\vec{\omega}_{21}\times\vec{L}_O=-mb^2\Omega^2\vec{\jmath}_2$

Por tanto, tenemos la reducción dinámica

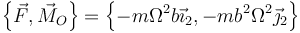
$\left\{\vec{F},\vec{M}_O\right\}=\left\{-m\Omega^2b\vec{\imath}_2,-mb^2\Omega^2\vec{\jmath}_2\right\}$

El momento resultante no es nulo, pero sí ortogonal a la fuerza resultante. Por tanto el sistema equivale a una fuerza única.

2 Momento de inercia de un cilindro

¿Cuánto vale el momento de inercia de un cilindro macizo homogéneo, de masa m, radio R y altura H, alrededor de un eje perpendicular a su cara lateral por el centro? (¡No haga integrales! Piense)

A $m (6 R 2 + H 2) / 12$
B $m R 2 / 2 + m H 2 / 3$
C $m (3 R 2 + H 2) / 12$
D $m (R 2 + H 2) / 4$

Solución

La respuesta correcta es la C.

3 Disco arrastrado por una barra

Se tiene un disco “2” de radio R que puede rodar sin deslizar sobre una superficie horizontal “1”. Un punto P del disco, situado a 0.5R del centro O, está unido por una varilla articulada “3” de longitud 2.5R a un pasador B, el cual se mueve con velocidad constante 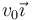$v_0 \vec{\imath}$ sobre un eje horizontal situado a 2R sobre O. En un momento dado, el punto P está sobre la misma horizontal que O (ver figura). Para ese instante y empleando los ejes indicados…

3.1 Pregunta 1

¿Cuánto vale la velocidad angular 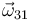$\vec{\omega}_{31}$ ?

A $\vec{0}$
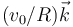
B $(v_0/R) \vec{k}$
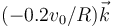
C $(-0.2v_0/R) \vec{k}$
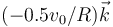
D $(-0.5v_0/R) \vec{k}$

Solución

La respuesta correcta es la C.

3.2 Pregunta 2

¿Dónde se encuentra el Centro Instantáneo de Rotación del movimiento {31}?

A En $( - 0.5 R,0)$
B En $(R, - 3 R)$
C En $(R,2 R)$
D En el infinito en la dirección vertical.

Solución

La respuesta correcta es la B.

3.3 Pregunta 3

¿Cuánto vale la velocidad del centro del disco, 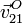$\vec{v}_{21}^O$ ?

A $\vec{0}$
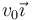
B $v_0 \vec{\imath}$
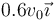
C $0.6v_0 \vec{\imath}$
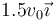
D $1.5v_0 \vec{\imath}$

Solución

La respuesta correcta es la C.

4 Percusión sobre cuerpo redondo

Un cuerpo redondo de masa m y radio R, con momento de inercia $I = γ m R 2$ , respecto a un eje ortogonal al plano por su centro, se encuentra en reposo situado sobre un plano horizontal. El cuerpo puede rodar sin deslizar sobre el plano horizontal. En un instante dado, se le aplica hacia adelante una percusión de módulo $P 0$ y que forma un ángulo β con la horizontal. Esta percusión se aplica en un punto del diámetro a la misma altura que el centro G del disco.

4.1 Pregunta 1

Para el instante inmediatamente posterior a la percusión, ¿cómo es la velocidad del centro del rodillo?

A Hacia adelante.
B Hacia atrás.
C Hacia adelante si β < 45° y hacia atrás si β > 45°.
D Hacia adelante o hacia atrás, con un signo que depende del valor de γ.

Solución

La respuesta correcta es la C.

4.2 Pregunta 2

Según el valor de β, ¿cómo es la percusión de reacción que se produce en el punto A de contacto del disco con el suelo?

A Siempre en la dirección de la recta que pasa por A y G.
B Siempre en la dirección de la recta que pasa por A y B.
C Tiene una componente vertical hacia arriba, y una horizontal que puede ir hacia adelante o hacia atrás.
D Tiene una componente vertical hacia arriba y una horizontal siempre hacia atrás, siendo la dirección dependiente de β.

Solución

La respuesta correcta es la D.

5 Número de grados de libertad

Una partícula de masa m se encuentra ensartada simultáneamente en dos varillas giratorias que se mueven en el plano OXY, como indica la figura.

¿Cuántos grados de libertad tiene la partícula?

A 0.
B 1.
C 2.
D 3.

Solución

La respuesta correcta es la A.

6 Movimiento instantáneo de un sólido

Un sólido se mueve de manera que el origen de coordenadas tiene velocidad, en m/s, 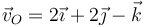$\vec{v}_O=2\vec{\imath}+2\vec{\jmath}-\vec{k}$ . La velocidad angular del sólido es 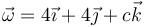$\vec{\omega}=4\vec{\imath}+4\vec{\jmath}+c\vec{k}$ . Si sabemos que el movimiento es de rotación, ¿cuánto vale c?

A $c = - 2$ .
B $c = 16$ .
C No hay suficiente información para hallar c.
D $c = 0$ .

Solución

La respuesta correcta es la B.

7 Desplazamientos virtuales

Una partícula se mueve en el plano OXY de manera que sus coordenadas polares cumplen, en todo momento,

ρ = ρ 0 e (b θ + Ω t)

¿Qué ecuación cumplen los desplazamientos virtuales de esta partícula?

A 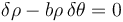$\delta\rho{}-b\rho{}\,\delta\theta=0$ .
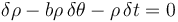B $\delta\rho{}-b\rho{}\,\delta\theta-Ω\rho{}\,\delta t=0$ .
C 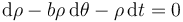$\mathrm{d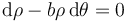}\rho{}-b\rho{}\,\mathrm{d}\theta-Ω\rho{}\,\mathrm{d}t=0$ .
D $\mathrm{d}\rho{}-b\rho{}\,\mathrm{d}\theta=0$ .

Solución

La respuesta correcta es la A.

8 Sistema de poleas

Se tiene el sistema de poleas de la figura. Las poleas son todas ideales (sin masa y sin rozamiento) y de ellas penden las masas indicadas.

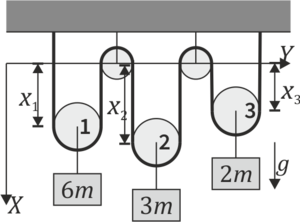
8.1 Pregunta 1

¿Cuál de las siguientes es una expresión de la lagrangiana del sistema, en un sistema mínimo de coordenadas (tantas como grados de libertad)?

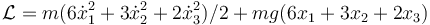
A $\mathcal{L}=m(6\dot{x}_1^2+3\dot{x}_2^2+2\dot{x}_3^2 )/2+mg(6x_1+3x_2+2x_3 )$
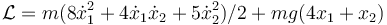
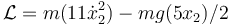
B $\mathcal{L}=m(8\dot{x}_1^2+4\dot{x}_1 \dot{x}_2+5\dot{x}_2^2 )/2+mg(4x_1+x_2 )$
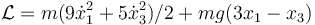
C $\mathcal{L}=m(11\dot{x}_2^2 )-mg(5x_2 )/2$
D $\mathcal{L}=m(9\dot{x}_1^2+5\dot{x}_3^2 )/2+mg(3x_1-x_3 )$

Solución

La respuesta correcta es la B.

8.2 Pregunta 2

¿Cuánto valen las aceleraciones de cada una de las masas en este sistema?

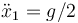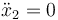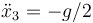
A $\ddot{x}_1=g/2$ , $\ddot{x}_2=0$ , $\ddot{x}_3=-g/2$
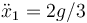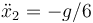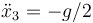
B $\ddot{x}_1=2g/3$ , $\ddot{x}_2=-g/6$ , $\ddot{x}_3=-g/2$
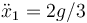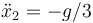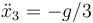
C $\ddot{x}_1=2g/3$ , $\ddot{x}_2=-g/3$ , $\ddot{x}_3=-g/3$
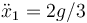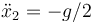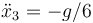
D $\ddot{x}_1=2g/3$ , $\ddot{x}_2=-g/2$ , $\ddot{x}_3=-g/6$

Solución

La respuesta correcta es la A.

@@ Línea 26: / Línea 26: @@
 El teorema de la cantidad de movimiento nos da la fuerza
-<center><math>\vec{F}=\left.\frac{\mathrm{d}\vec{p}}{\mathrm{d}t}\right|_1=\overbrace{\left.\frac{\mathrm{d}\vec{p}}{\mathrm{d}t}\right|_2}^{=\vec{0}}+\vec{\omega}_{21}\times\vec{p}=-m\Omega^b\vec{\imath}_2</math></center>
+<center><math>\vec{F}=\left.\frac{\mathrm{d}\vec{p}}{\mathrm{d}t}\right|_1=\overbrace{\left.\frac{\mathrm{d}\vec{p}}{\mathrm{d}t}\right|_2}^{=\vec{0}}+\vec{\omega}_{21}\times\vec{p}=-m\Omega^2b\vec{\imath}_2</math></center>
 Se puede llegar a este resultado simplemente observando que P describe un movimiento circular uniforme alrededor del eje OZ.

Examen parcial CMR 19-20

De Laplace

Revisión de 12:32 7 feb 2020

Contenido

1 Rotor de una sola masa

2 Momento de inercia de un cilindro

3 Disco arrastrado por una barra

3.1 Pregunta 1

3.2 Pregunta 2

3.3 Pregunta 3

4 Percusión sobre cuerpo redondo

4.1 Pregunta 1

4.2 Pregunta 2

5 Número de grados de libertad

6 Movimiento instantáneo de un sólido

7 Desplazamientos virtuales

8 Sistema de poleas

8.1 Pregunta 1

8.2 Pregunta 2

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES