Problemas de Ondas sonoras
De Laplace
(→Tiempo de un sonido en llegar al suelo) |
(→Batidos por diferencia de temperaturas) |
||
| Línea 17: | Línea 17: | ||
===Batidos por diferencia de temperaturas=== | ===Batidos por diferencia de temperaturas=== | ||
| - | Determine la longitud de un tubo de | + | Determine la longitud de un tubo de órgano cerrado por uno de sus extremos y abierto por el otro, si debe producir una nota de 440 Hz a 25 ºC. Admita que la velocidad del sonido en el aire a temperaturas próximas a la ambiente depende de la temperatura como |
| - | producir una nota de | + | |
| - | Admita que la velocidad del sonido en el aire a temperaturas | + | <center><math>c = 331\,\frac{\mathrm{m}}{\mathrm{s}} + 0.6\,\frac{\mathrm{s}}{\mathrm{s}\cdot^\circ\mathrm{C}}T_C</math></center> |
| - | como | + | |
| - | c = | + | con <math>T_C</math> la temperatura en grados centígrados. Si un trombón debe tocar la misma nota de 440 Hz que el órgano y el trombón está a 25 ºC, pero el órgano se encuentra sólo a 15 ºC, ¿cu´al es la frecuencia de los batidos que se escuchan? |
| - | + | ||
| - | con | + | |
| - | Si un | + | |
| - | encuentra | + | |
[[Categoría:Problemas de ondas sonoras|0]] | [[Categoría:Problemas de ondas sonoras|0]] | ||
[[Categoría:Problemas de Física Aeronáuticos|120]] | [[Categoría:Problemas de Física Aeronáuticos|120]] | ||
[[Categoría:Ondas sonoras]] | [[Categoría:Ondas sonoras]] | ||
Revisión de 16:07 12 mar 2009
Contenido |
1 Duración de un trueno
Un rayo cae desde una nube situada a 2 km de altura. Si el rayo cae verticalmente e impacta de forma casi instantánea en un punto situado a 10 km de un observador, ¿cuánto tarda un el trueno en llegar a este observador? ¿Cuánto dura este trueno? Suponga que el aire se encuentra a 20 ºC.
2 Onda sonora en agua
Un barco usa un sistema de sonar para detectar objetos submarinos. El barco se encuentra en reposo en una zona en la que la profundidad del lecho marino es de 50 metros. El sistema emite un haz de ondas de sonido de frecuencia f = 262 Hz que forma un ángulo de 30º con la superficie del mar y mide el tiempo que tarda la onda, que se refleja en un pecio, en regresar al detector. Sabiendo que el tiempo de retardo es 0.135 segundos y que la densidad del agua es 1.06×10³ kg/m³, calcule
- la velocidad del sonido en el agua
- el módulo de compresibilidad del agua
- la longitud de onda de la señal emitida.
3 Tiempo de un sonido en llegar al suelo
La temperatura de la atmósfera en sus capas bajas decrece con la altura como

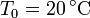
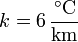
Un avión rompe la barrera del sonido cuando se encuentra a 8 km de altura. ¿Cuánto tarda el estampido sónico en llegar al suelo?
4 Batidos por diferencia de temperaturas
Determine la longitud de un tubo de órgano cerrado por uno de sus extremos y abierto por el otro, si debe producir una nota de 440 Hz a 25 ºC. Admita que la velocidad del sonido en el aire a temperaturas próximas a la ambiente depende de la temperatura como
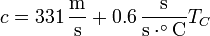
con TC la temperatura en grados centígrados. Si un trombón debe tocar la misma nota de 440 Hz que el órgano y el trombón está a 25 ºC, pero el órgano se encuentra sólo a 15 ºC, ¿cu´al es la frecuencia de los batidos que se escuchan?





