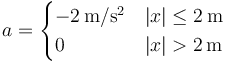|
|
| (6 ediciones intermedias no se muestran.) |
| Línea 1: |
Línea 1: |
| - | ==Enunciado==
| |
| | Una partícula se mueve sobre una recta partiendo desde <math>x_0=-5\,\mathrm{m}</math> con velocidad <math>v_0=+3\,\mathrm{m}/\mathrm{s}</math>. En su movimiento, experimenta la aceleración | | Una partícula se mueve sobre una recta partiendo desde <math>x_0=-5\,\mathrm{m}</math> con velocidad <math>v_0=+3\,\mathrm{m}/\mathrm{s}</math>. En su movimiento, experimenta la aceleración |
| | | | |
| Línea 13: |
Línea 12: |
| | > 2\,\mathrm{m}\end{cases} | | > 2\,\mathrm{m}\end{cases} |
| | </math></center> | | </math></center> |
| - | ==Velocidad en x = 7 m==
| |
| - | Esta pregunta (y la siguiente) se puede resolver empleando la ecuación del movimiento uniforme y del movimiento uniformemente acelerado, pero también empleando otras que evitan el cálculo en función del tiempo.
| |
| - |
| |
| - | La aceleración en un [[Cinemática_del_movimiento_rectilíneo_(GIOI)#Uniformemente_acelerado|movimiento uniformemente acelerado]] cumple
| |
| - |
| |
| - | <center><math>a = \frac{v_3^2-v_1^2}{2(x_3-x_1)}</math></center>
| |
| - |
| |
| - | La zona donde hay aceleración va de <math>x_1 = -2\,\mathrm{m}</math> a <math>x_3 = +2\,\mathrm{m}</math>, siendo la velocidad de entrada <math>v_1=+3\mathrm{m}/\mathrm{s}</math> y la aceleración +2m/s². Esto nos da, en el SI
| |
| - |
| |
| - | <center><math>2 = \frac{v_3^2-3^2}{2\cdot 4}\qquad\Rightarrow\qquad v_3^2 = 9+2\times 8 = 25\qquad\Rightarrow\qquad v_3 = 5\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
| |
| - |
| |
| - | A partir de ahí y hasta <math>x=7\,\mathrm{m}</math> la velocidad es constante e igual a <math>v_3 = 5\,{\mathrm{m}}/{\mathrm{s}}</math>
| |
| - |
| |
| - | ==Velocidad media==
| |
| - | El movimiento se compone de tres tramos, siendo el desplazamiento total
| |
| - |
| |
| - | <center><math>\Delta x = \Delta x_1 + \Delta x_2 + \Delta x_3 = 3\,\mathrm{m}+4\,\mathrm{m}+5\,\mathrm{m}=12\,\mathrm{m}</math></center>
| |
| - |
| |
| - | El primer tramo mide 3m y se recorre a una velocidad constante de 3m/s, por lo que
| |
| - |
| |
| - | <center><math>\Delta t_1 = \frac{\Delta x_1}{v_1}=1\,\mathrm{s}</math></center>
| |
| - |
| |
| - | El primer tramo mide 5m y se recorre a una velocidad constante de 5m/s, por lo que
| |
| - |
| |
| - | <center><math>\Delta t_3 = \frac{\Delta x_3}{v_3}=1\,\mathrm{s}</math></center>
| |
| - |
| |
| - | El segundo tramo se recorre con un movimiento uniformemente acelerado. Para este movimiento la velocidad media es
| |
| - |
| |
| - | <center><math>v_{m2}=\frac{v_1+v_2}{2}=4\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
| |
| - |
| |
| - | y por tanto, el tiempo que se tarda en recorrer esta zona es
| |
| - |
| |
| - | <center><math>\Delta t_2 = \frac{\Delta x_2}{v_{m2}}= 1\,\mathrm{s}</math></center>
| |
| - |
| |
| - | Por tanto, el intervalo total dura
| |
| - |
| |
| - | <center><math>\Delta t = (1+1+1)\mathrm{s}=3\,\mathrm{s}</math></center>
| |
| - |
| |
| - | lo que nos da la velocidad media
| |
| - |
| |
| - | <center><math>v_m = \frac{\Delta x}{\Delta t}=\frac{12\,\mathrm{m}}{3\,\mathrm{s}}=4\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
| |
| - |
| |
| - | ==Caso de aceleración negativa==
| |
| - | Cuando se aplica la misma lógica del primer apartado al nuevo caso, obtenemos
| |
| - |
| |
| - | <center><math>-2 = \frac{v_3^2-3^2}{2\cdot 4}\qquad\Rightarrow\qquad v_3^2 = 9+2\times 8=-7</math></center>
| |
| - |
| |
| - | pero este resultado no tiene sentido, ya que sale un cuadrado negativo.
| |
| - |
| |
| - | ¿Qué ocurre aquí? Que, en este caso, la partícula nunca llega a <math>x=+2\,\mathrm{m}</math> y, por tanto, tampoco a <math>x=+7\,\mathrm{m}</math>.
| |
| - |
| |
| - | Al ser la aceleración negativa, lo que ocurre es que la velocidad de la partícula empieza a disminuir hasta hacerse 0 en un punto de retorno, y a partir de ahí la velocidad se hace negativa, con lo que la partícula vuelve a salir por donde había venido.
| |
| - |
| |
| - | El punto de retorno es aquél para el cual la velocidad es cero.
| |
| - |
| |
| - | <center><math>-2 = \frac{0^2-3^2}{2\cdot (x_\mathrm{max}-(-2)}))\qquad\Rightarrow\qquad x_\mathrm{max} = -2+\frac{9}{4}=0.25\,\mathrm{m}</math></center>
| |
con velocidad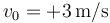 
. En su movimiento, experimenta la aceleración
?
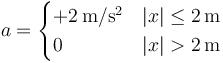
