Distancia mínima entre dos rectas
De Laplace
(→Enunciado) |
(→Cálculo de los puntos más próximos) |
||
| (9 ediciones intermedias no se muestran.) | |||
| Línea 2: | Línea 2: | ||
Hallar la menor distancia entre las rectas <math>\Delta(A,B)</math> y <math>\Gamma(C,D)</math>, y determinar el vector (segmento orientado) de menor módulo que une ambas rectas. Las coordenadas cartesianas de los puntos que definen dichas rectas vienen dadas por las ternas <math>A(1,-2,-1)</math> y <math>B(4,0,-3)</math>, para el caso de <math>\Delta</math>, y <math>C(1,2,-1)</math> y <math>D(2,-4,-5)</math>, para la recta <math>\Gamma.</math> | Hallar la menor distancia entre las rectas <math>\Delta(A,B)</math> y <math>\Gamma(C,D)</math>, y determinar el vector (segmento orientado) de menor módulo que une ambas rectas. Las coordenadas cartesianas de los puntos que definen dichas rectas vienen dadas por las ternas <math>A(1,-2,-1)</math> y <math>B(4,0,-3)</math>, para el caso de <math>\Delta</math>, y <math>C(1,2,-1)</math> y <math>D(2,-4,-5)</math>, para la recta <math>\Gamma.</math> | ||
| + | == Solución == | ||
| + | Podemos construir un plano que sea paralelo a las dos rectas y que | ||
| + | contenga a una de ellas, por ejemplo <math>\Delta</math>. El vector normal a este plano debe ser | ||
| + | perpendicular a las dos rectas. Por tanto podemos escoger el producto | ||
| + | vectorial de los vectores que definen las rectas | ||
| + | <center><math> | ||
| + | \vec{a} = \overrightarrow{AB}\times\overrightarrow{CD} = | ||
| + | \left| | ||
| + | \begin{array}{ccc} | ||
| + | \vec{\imath} & \vec{\jmath} & \vec{k}\\ | ||
| + | 3 & 2 &-2\\ | ||
| + | 1 & -6 & -4 | ||
| + | \end{array} | ||
| + | \right|=-20\vec{\imath}+10\vec{\jmath}-20\vec{k} | ||
| + | </math></center> | ||
| + | Ahora bien, todos los puntos de la recta <math>\Gamma</math> están a la misma | ||
| + | distancia de este plano, entre ellos el más cercano a la recta | ||
| + | <math>\Delta</math>. Por tanto la distancia entre las dos rectas es la distancia | ||
| + | de la recta <math>\Gamma</math> a este plano. Pero vimos en el problema anterior | ||
| + | que la distancia de un punto a un plano es la proyección sobre el | ||
| + | vector perpendicular al plano de un vector con un extremo en el punto | ||
| + | y otro en el plano. Como nos vale cualquier punto de la recta <math>\Gamma</math> | ||
| + | y cualquier punto del plano, podemos escoger como vector el | ||
| + | <math>\overrightarrow{CA}</math>. Así pues, la distancia entre las dos rectas es | ||
| + | <center><math> | ||
| + | d(\Delta,\Gamma) = \dfrac{{\overrightarrow{CA}}\cdot{\vec{a}}}{|\vec{a}|} | ||
| + | = | ||
| + | \dfrac{{\overrightarrow{CA}}\cdot({\overrightarrow{AB}\times{\overrightarrow{CD}})}}{|\overrightarrow{AB}\times{\overrightarrow{CD}|}} | ||
| + | = -\dfrac{4}{3} | ||
| + | </math></center> | ||
| + | El signo menos aparece por la orientación escogida de los vectores. La | ||
| + | distancia es simplemente el valor absoluto, | ||
| + | <center><math> | ||
| + | d(\Delta,\Gamma) = \dfrac{4}{3}\,\mathrm{m} | ||
| + | </math></center> | ||
| + | El vector de menor módulo que une las dos rectas es el que tiene la | ||
| + | dirección de <math>\vec{a}</math> con módulo 4/3, es decir | ||
| + | <center><math> | ||
| + | \vec{n} = \dfrac{4}{3}\dfrac{\vec{a}}{|\vec{a}|}= | ||
| + | -\dfrac{8}{9}\vec{\imath}+\dfrac{4}{9}\vec{\jmath}-\dfrac{8}{9}\vec{k} | ||
| + | </math></center> | ||
| + | |||
| + | == Cálculo de los puntos más próximos == | ||
| + | Para determinar los puntos de las rectas <math>\Delta</math> y <math>\Gamma</math> que une | ||
| + | este vector podemos hacer lo siguiente. Un punto genérico de estas | ||
| + | rectas es | ||
| + | <center> | ||
| + | <math> | ||
| + | \begin{array}{lll} | ||
| + | \overrightarrow{OP}_{\Delta} = \overrightarrow{OA} + \delta\overrightarrow{AB} = | ||
| + | \left\{ | ||
| + | \begin{array}{l} | ||
| + | x=1 + 3\delta\\ | ||
| + | y=-2+2\delta\\ | ||
| + | z=-1-2\delta | ||
| + | \end{array} | ||
| + | \right.&& | ||
| + | \overrightarrow{OP}_{\Gamma} = \overrightarrow{OC} + \gamma\overrightarrow{CD} = | ||
| + | \left\{ | ||
| + | \begin{array}{l} | ||
| + | x=1 + \gamma\\ | ||
| + | y=2-6\gamma\\ | ||
| + | z=-1-4\gamma | ||
| + | \end{array} | ||
| + | \right. | ||
| + | \end{array} | ||
| + | </math> | ||
| + | </center> | ||
| + | Así pues, el vector que une dos puntos cualquiera de las rectas es | ||
| + | <center><math> | ||
| + | \overrightarrow{P_{\Delta}P_{\Gamma}} = | ||
| + | (\gamma-3\delta)\vec{\imath} + | ||
| + | (4-6\gamma-2\delta)\vec{\jmath}+(-4\gamma+2\delta)\vec{k} | ||
| + | </math></center> | ||
| + | Los puntos <math>P^*_{\Delta}</math> y <math>P^*_{\Gamma}</math> que están mas cerca uno de otro son tales que el vector <math>\overrightarrow{P^*_{\Delta}P^*_{\Gamma}}</math> es paralelo a <math>\vec{n}</math>. | ||
| + | Imponiendo esta condición nos queda un | ||
| + | sistema de tres ecuaciones con dos incógnitas | ||
| + | <center><math> | ||
| + | \vec{n}\times \overrightarrow{P^*_{\Delta}P^*_{\Gamma}} = \vec{0} | ||
| + | \Longrightarrow | ||
| + | \begin{array}{l} | ||
| + | 9\gamma-27\delta + 8 =0\\ | ||
| + | 54\gamma+18\delta - 32 =0\\ | ||
| + | 36\gamma-18\delta - 8 =0 | ||
| + | \end{array} | ||
| + | </math></center> | ||
| + | El determinante de este sistema es nulo, lo cual indica que una de las | ||
| + | ecuaciones es combinación lineal de las otras dos. Eliminando una de | ||
| + | ellas y resolviendo el sistema se obtiene | ||
| + | <center><math> | ||
| + | \gamma=\delta=4/9 | ||
| + | </math></center> | ||
| + | Sustituyendo obtenemos los puntos de las rectas | ||
| + | unidos por el vector de menor módulo, <math>\vec{n}</math> | ||
| + | <center> | ||
| + | <math> | ||
| + | \begin{array}{lll} | ||
| + | P_{\Delta} = (7/3,-10/9,-17/9)&& | ||
| + | P_{\Gamma} = (13/9,-2/3,-25/9) | ||
| + | \end{array} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | ===Método alternativo de resolución=== | ||
| + | |||
| + | Otra forma de atacar el problema es utilizar directamente la expresión que da la forma | ||
| + | general de un vector que uno dos puntos cualesquiera de las rectas en función de dos parámetros. El vector | ||
| + | pedido en el enunciado es aquel cuyo módulo es mínimo, es decir, hemos de exigir | ||
| + | <center><math> | ||
| + | |\overrightarrow{P_{\Delta}P_{\Gamma}}|\quad\mathrm{minimo}\Rightarrow |\overrightarrow{P_{\Delta}P_{\Gamma}}|^2\quad\mathrm{minimo} | ||
| + | </math></center> | ||
| + | Esto es, hay que encontrar un mínimo de la función de dos variables | ||
| + | <center><math> | ||
| + | f(\delta,\gamma)=|\overrightarrow{P_{\Delta}P_{\Gamma}}|^2 = (3\delta-\gamma)^2+(2\delta+6\gamma-4)^2+(4\gamma-2\delta)^2= | ||
| + | 16-16\delta+17\delta^2-48\gamma+53\gamma^2+2\delta\gamma | ||
| + | </math></center> | ||
| + | La condición para encontrar un mínimo es que las derivadas parciales respecto a los parámetros se anulen. | ||
| + | Es decir | ||
| + | <center><math> | ||
| + | \left. | ||
| + | \begin{array}{l} | ||
| + | \frac{\displaystyle\partial f}{\displaystyle\partial\delta}=34\delta+2\gamma-16=0\\ \\ | ||
| + | \frac{\displaystyle\partial f}{\displaystyle\partial\gamma}=2\delta+106\gamma-48=0 | ||
| + | \end{array} | ||
| + | \right. | ||
| + | </math></center> | ||
| + | Resolviendo este sistema de dos ecuaciones para dos incógnitas encontramos que el valor de los parámetros | ||
| + | para el cual la distancia entre los puntos de la recta es mínima son | ||
| + | <center><math> | ||
| + | \delta=\gamma=\dfrac{4}{9} | ||
| + | </math></center> | ||
| + | Vemos que son los mismos valores que hallamos con el método anterior, como es lógico. A partir de aquí | ||
| + | obtendríamos el vector buscado sustituyendo los valores en las rectas para obtener los puntos y unirlos con | ||
| + | el vector buscado. | ||
| + | |||
| + | |||
| + | [[Categoría:Vectores libres|0]] | ||
[[Categoría: Problemas de vectores libres (G.I.A.)]] | [[Categoría: Problemas de vectores libres (G.I.A.)]] | ||
| + | [[Categoría:Física I (G.I.T.I.)]] | ||
| + | [[Categoría:Física I (G.I.C.)]] | ||
| + | [[Categoría:Problemas de Álgebra Vectorial]] | ||
última version al 15:50 29 sep 2019
Contenido |
1 Enunciado
Hallar la menor distancia entre las rectas Δ(A,B) y Γ(C,D), y determinar el vector (segmento orientado) de menor módulo que une ambas rectas. Las coordenadas cartesianas de los puntos que definen dichas rectas vienen dadas por las ternas A(1, − 2, − 1) y B(4,0, − 3), para el caso de Δ, y C(1,2, − 1) y D(2, − 4, − 5), para la recta Γ.
2 Solución
Podemos construir un plano que sea paralelo a las dos rectas y que contenga a una de ellas, por ejemplo Δ. El vector normal a este plano debe ser perpendicular a las dos rectas. Por tanto podemos escoger el producto vectorial de los vectores que definen las rectas
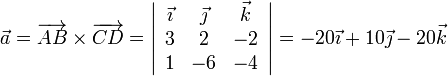
Ahora bien, todos los puntos de la recta Γ están a la misma
distancia de este plano, entre ellos el más cercano a la recta
Δ. Por tanto la distancia entre las dos rectas es la distancia
de la recta Γ a este plano. Pero vimos en el problema anterior
que la distancia de un punto a un plano es la proyección sobre el
vector perpendicular al plano de un vector con un extremo en el punto
y otro en el plano. Como nos vale cualquier punto de la recta Γ
y cualquier punto del plano, podemos escoger como vector el
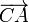 . Así pues, la distancia entre las dos rectas es
. Así pues, la distancia entre las dos rectas es
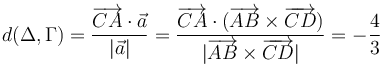
El signo menos aparece por la orientación escogida de los vectores. La distancia es simplemente el valor absoluto,
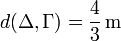
El vector de menor módulo que une las dos rectas es el que tiene la
dirección de  con módulo 4/3, es decir
con módulo 4/3, es decir
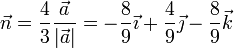
3 Cálculo de los puntos más próximos
Para determinar los puntos de las rectas Δ y Γ que une este vector podemos hacer lo siguiente. Un punto genérico de estas rectas es
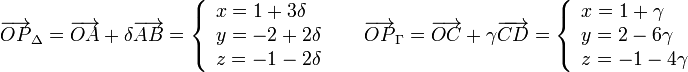
Así pues, el vector que une dos puntos cualquiera de las rectas es
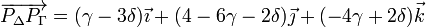
Los puntos 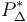 y
y 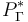 que están mas cerca uno de otro son tales que el vector
que están mas cerca uno de otro son tales que el vector 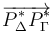 es paralelo a
es paralelo a 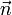 .
Imponiendo esta condición nos queda un
sistema de tres ecuaciones con dos incógnitas
.
Imponiendo esta condición nos queda un
sistema de tres ecuaciones con dos incógnitas
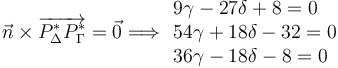
El determinante de este sistema es nulo, lo cual indica que una de las ecuaciones es combinación lineal de las otras dos. Eliminando una de ellas y resolviendo el sistema se obtiene
Sustituyendo obtenemos los puntos de las rectas
unidos por el vector de menor módulo, 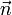

3.1 Método alternativo de resolución
Otra forma de atacar el problema es utilizar directamente la expresión que da la forma general de un vector que uno dos puntos cualesquiera de las rectas en función de dos parámetros. El vector pedido en el enunciado es aquel cuyo módulo es mínimo, es decir, hemos de exigir
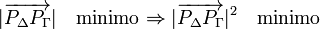
Esto es, hay que encontrar un mínimo de la función de dos variables
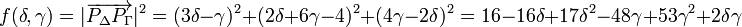
La condición para encontrar un mínimo es que las derivadas parciales respecto a los parámetros se anulen. Es decir
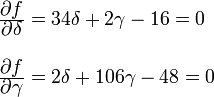
Resolviendo este sistema de dos ecuaciones para dos incógnitas encontramos que el valor de los parámetros para el cual la distancia entre los puntos de la recta es mínima son
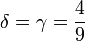
Vemos que son los mismos valores que hallamos con el método anterior, como es lógico. A partir de aquí obtendríamos el vector buscado sustituyendo los valores en las rectas para obtener los puntos y unirlos con el vector buscado.





