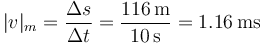Aceleración lineal con el tiempo (GIOI)
De Laplace
(Página creada con '==Enunciado== Una partícula de masa <math>m=2\,\mathrm{kg}</math> describe un movimiento rectilíneo en el que la aceleración, como función del tiempo sigue la gráfica de la…') |
(→Enunciado) |
||
| Línea 6: | Línea 6: | ||
# ¿Cuál es la distancia total recorrida entre <math>t=0\,\mathrm{s}</math> y <math>t=10\,\mathrm{s}</math>? | # ¿Cuál es la distancia total recorrida entre <math>t=0\,\mathrm{s}</math> y <math>t=10\,\mathrm{s}</math>? | ||
# ¿Cuánto vale la rapidez media en dicho intervalo? | # ¿Cuánto vale la rapidez media en dicho intervalo? | ||
| + | |||
| + | ==Rapidez== | ||
| + | Lo primero que debemos hacer es determinar la aceleración como función del tiempo, de ahí la velocidad y de ésta la posición. | ||
| + | |||
| + | La gráfica es la de una recta | ||
| + | |||
| + | <center><math>a=A+Bt\,</math></center> | ||
| + | |||
| + | que en <math>t=0\,\mathrm{s}</math> vale 3%thinsp;m/s² y en <math>t=2\,\mathrm{s}</math> vale 0. Sustituyendo estos dos valores hallamos A y B y resulta, en el SI | ||
| + | |||
| + | <center><math>a=3-\frac{3}{2}t</math></center> | ||
| + | |||
| + | Integrando esta aceleración obtenemos la velocidad | ||
| + | |||
| + | <center><math>v=v_0+\int_0^t a\,\mathrm{d}t=3t-\frac{3}{4}t^2</math></center> | ||
| + | |||
| + | La velocidad en <math>t=10\,\mathrm{s}</math> es | ||
| + | |||
| + | <center><math>v=\left(30-\frac{300}{4}\right)\,\frac{\mathrm{m}}{\mathrm{s}}=-45\,\frac{\mathrm{m}}{\mathrm{s}}</math></center> | ||
| + | |||
| + | y la rapidez | ||
| + | |||
| + | <center><math>|v|= +45\,\frac{\mathrm{m}}{\mathrm{s}}</math></center> | ||
| + | |||
| + | ==Velocidad media== | ||
| + | Para la velocidad media necesitamos el desplazamiento, para el cual primero debemos hallar la posición como función del tiempo | ||
| + | |||
| + | <center><math>x=x_0+\int_0^t v\,\mathrm{d}t=\frac{3}{2}t^2-\frac{1}{4}t^3</math></center> | ||
| + | |||
| + | que en <math>t=10\,\mathrm{s}</math> es | ||
| + | |||
| + | <center><math>x(10)= -100\,\mathrm{m}</math></center> | ||
| + | |||
| + | lo que nos da la velocidad media | ||
| + | |||
| + | <center><math>v_m= \frac{x(10)-x(0)}{10\,\mathrm{s}}=-10\,\mathrm{m}{\mathrm{s}}</math></center> | ||
| + | ==Distancia total recorrida== | ||
| + | La distancia recorrida no coincide con el desplazamiento porque la velocidad cambia de signo. | ||
| + | |||
| + | El cambio de signo se produce cuando la velocidad se anula lo que ocurre en | ||
| + | |||
| + | <center><math>3t-\frac{3}{4}t^2=0\qquad\Rightarrow\qquad \left\{\begin{array}{rcl}t & = & 0\,\mathrm{s} \\ && \\ t & = & 4\,\mathrm{s}\end{array}\right.</math></center> | ||
| + | |||
| + | El desplazamiento entre t = 0 s y t = 4 s es | ||
| + | |||
| + | <center><math>\Delta x_1 = x(4\,\mathrm{s})-x(0\,\mathrm{s})=\frac{3}{2}4^2-\frac{1}{4}4^3 = 8\,\mathrm{m}</math></center> | ||
| + | |||
| + | y entre t = 4 s y t = 10 s | ||
| + | |||
| + | <center><math>\Delta x_2 = x(10\,\mathrm{s})-x(4\,\mathrm{s})=-100-8 = -108\,\mathrm{m}</math></center> | ||
| + | |||
| + | Por tanto la distancia total recorrida vale | ||
| + | |||
| + | <center><math>\Delta s = |\Delta x_1|+|\Delta x_2| = 116\,\mathrm{m}</math></center> | ||
| + | |||
| + | ==Rapidez media== | ||
| + | La rapidez media es la distancia total recorrida dividida por el intervalo de tiempo empleado | ||
| + | |||
| + | <center><math>|v|_m=\frac{\Delta s}{\Delta t}=\frac{116\,\mathrm{m}}{10\,\mathrm{s}}=1.16\,\mathrm{m}{\mathrm{s}}</math></center> | ||
Revisión de 18:01 24 sep 2019
Contenido |
1 Enunciado
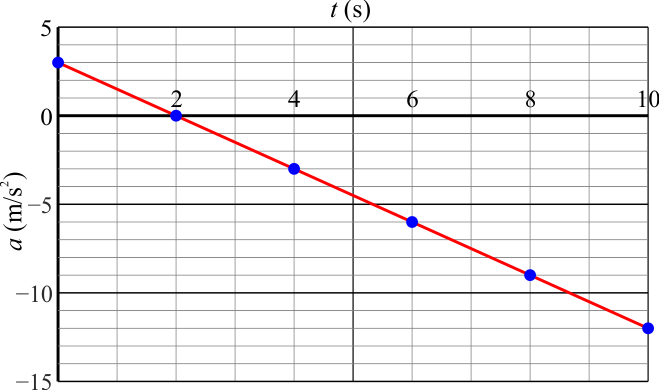
Una partícula de masa 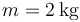 describe un movimiento rectilíneo en el que la aceleración, como función del tiempo sigue la gráfica de la figura. La partícula parte en
describe un movimiento rectilíneo en el que la aceleración, como función del tiempo sigue la gráfica de la figura. La partícula parte en  del reposo en x = 0.
del reposo en x = 0.
- ¿Cuánto vale la rapidez de la partícula en
 ?
?
- ¿Cuál es su velocidad media entre
 y
y  ?
?
- ¿Cuál es la distancia total recorrida entre
 y
y  ?
?
- ¿Cuánto vale la rapidez media en dicho intervalo?
2 Rapidez
Lo primero que debemos hacer es determinar la aceleración como función del tiempo, de ahí la velocidad y de ésta la posición.
La gráfica es la de una recta
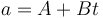
que en  vale 3%thinsp;m/s² y en
vale 3%thinsp;m/s² y en  vale 0. Sustituyendo estos dos valores hallamos A y B y resulta, en el SI
vale 0. Sustituyendo estos dos valores hallamos A y B y resulta, en el SI

Integrando esta aceleración obtenemos la velocidad
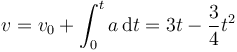
La velocidad en  es
es
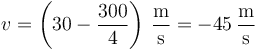
y la rapidez

3 Velocidad media
Para la velocidad media necesitamos el desplazamiento, para el cual primero debemos hallar la posición como función del tiempo
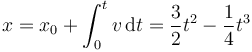
que en  es
es
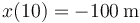
lo que nos da la velocidad media
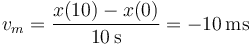
4 Distancia total recorrida
La distancia recorrida no coincide con el desplazamiento porque la velocidad cambia de signo.
El cambio de signo se produce cuando la velocidad se anula lo que ocurre en
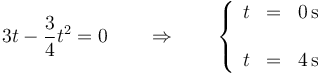
El desplazamiento entre t = 0 s y t = 4 s es
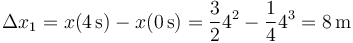
y entre t = 4 s y t = 10 s

Por tanto la distancia total recorrida vale
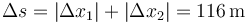
5 Rapidez media
La rapidez media es la distancia total recorrida dividida por el intervalo de tiempo empleado