Persecución policial (GIOI)
De Laplace
(→Alcance) |
(Página creada con '==Enunciado== Las especificaciones del Seat Exeo establecen que va de 0 a 100 km/h en 9.2 s. ¿Cuánto vale su aceleración media en este periodo? ¿Cuánto vale e…') |
||
| (3 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| - | Las especificaciones del | + | Las especificaciones del Seat Exeo establecen que va de 0 a 100 km/h en 9.2 s. ¿Cuánto vale su aceleración media en este periodo? ¿Cuánto vale el tiempo mínimo para atravesar un cruce de 15 m de anchura, si parte de estar parado en un semáforo? ¿Con qué velocidad llegaría al otro lado? |
| - | Un Seat León FR amarillo circula por la carretera a 160 km/h y pasa junto a un coche de la Guardia Civil parado en el arcén. Sabiendo que la benemérita usa un | + | Un Seat León FR amarillo circula por la carretera a 160 km/h y pasa junto a un coche de la Guardia Civil parado en el arcén. Sabiendo que la benemérita usa un Seat Exeo, ¿cuál es el mínimo tiempo que tarda en alcanzar al Seat León si este no reduce su velocidad? ¿A qué distancia del punto donde estába parado lo alcanza? ¿Qué velocidad tiene el coche patrulla cuando alcanza al infractor? |
==Aceleración media== | ==Aceleración media== | ||
La aceleración media la hallamos a partir del cociente entre el incremento de la velocidad y el tiempo empleado en este incremento | La aceleración media la hallamos a partir del cociente entre el incremento de la velocidad y el tiempo empleado en este incremento | ||
| - | <center><math>a_m = \frac{\Delta v}{\Delta t} = \frac{100\,\mathrm{km}/ | + | <center><math>a_m = \frac{\Delta v}{\Delta t} = \frac{100\,\mathrm{km}/h-100\,\mathrm{km}/h}{9.2\,\mathrm{s}}</math></center> |
| - | Aquí el único problema es la mezcla de unidades | + | Aquí el único problema es la mezcla de unidades, que resolvemos introduciendo los factores de conversión |
| - | <center><math>a_m = \frac{\ | + | <center><math>a_m = \frac{100}{9.2}\,\left(\frac{\mathrm{km}}{\mathrm{h}}\right)\times\left(\frac{1}{\mathrm{s}}\right)\times\left(\frac{1000\,\mathrm{m}}{1\,\mathrm{km}}\right)\times\left(\frac{1\,\mathrm{h}}{3600\,\mathrm{s}}\right) = 3.02\,\frac{\mathrm{m}}{\mathrm{s}^2}</math></center> |
| - | Esto equivale a una aceleración de 0. | + | Esto equivale a una aceleración de 0.31g, que no es muy intensa. |
| - | Para atravesar un cruce de 15 | + | Para atravesar un cruce de 15\,m en máxima aceleración partiendo del reposo serequiere un tiempo |
| - | <center><math>\Delta x = \frac{1}{2}at^2\qquad\Rightarrow\qquad t = \sqrt{\frac{2\Delta x}{ | + | <center><math>\Delta x = \frac{1}{2}at^2\qquad\Rightarrow\qquad t = \sqrt{\frac{2\Delta x}{g}}=3.2\,\mathrm{s}</math></center> |
y la velocidad al llegar al otro lado del cruce es | y la velocidad al llegar al otro lado del cruce es | ||
| - | <center><math>v = a t = \sqrt{2a\,\Delta x}=9. | + | <center><math>v = a t = \sqrt{2a\,\Delta x}=9.5\,\frac{\mathrm{m}}{\mathrm{s}}=34\,\frac{\mathrm{km}}{\mathrm{h}}</math></center> |
==Alcance== | ==Alcance== | ||
La forma más rápida que tiene el coche patrulla de alcanzar al infractor es marchando a máxima aceleración. Si levantan el pie del acelerador, la velocidad se incrementará más lentamente y por tanto tardará más en alcanzarlo. | La forma más rápida que tiene el coche patrulla de alcanzar al infractor es marchando a máxima aceleración. Si levantan el pie del acelerador, la velocidad se incrementará más lentamente y por tanto tardará más en alcanzarlo. | ||
| - | Si admitimos que el | + | Si admitimos que el Exeo es capaz de mantener la aceleración que hemos calculado antes durante un tiempo largo, el alcance se produce cuando la distancia recorrida por el Exeo es la misma que la recorrida por el León, esto es |
<center><math>\frac{1}{2}at^2 = v_L t</math></center> | <center><math>\frac{1}{2}at^2 = v_L t</math></center> | ||
| Línea 36: | Línea 36: | ||
esto nos da el tiempo de alcance | esto nos da el tiempo de alcance | ||
| - | <center><math>t_a = \frac{2v_L}{a} = | + | <center><math>t_a = \frac{2v_L}{a} = 29.4\,\mathrm{s}</math></center> |
La distancia recorrida hasta el alcance vale | La distancia recorrida hasta el alcance vale | ||
| - | <center><math>\Delta x = \frac{1}{2}at_a^2 = v_L t_a = | + | <center><math>\Delta x = \frac{1}{2}at_a^2 = v_L t_a = 1310\,\mathrm{m}</math></center> |
| - | Ahora bien, ¿cuál es la velocidad instantánea del | + | Ahora bien, ¿cuál es la velocidad instantánea del Exeo en este momento? La media es la misma, pues ha recorrido la misma distancia en el mismo tiempo, pero puesto que partía del reposo, la instantánea debe ser mayor. Concretamente |
<center><math>v_{GC} = a t_a = 88.9\,\frac{\mathrm{m}}{\mathrm{s}} = 320\,\frac{\mathrm{km}}{\mathrm{h}}</math></center> | <center><math>v_{GC} = a t_a = 88.9\,\frac{\mathrm{m}}{\mathrm{s}} = 320\,\frac{\mathrm{km}}{\mathrm{h}}</math></center> | ||
| - | lo cual es absurdo, pues se trata de un | + | lo cual es absurdo, pues se trata de un Seat Exeo, no de un Fórmula 1. |
Este problema no es realista en cuanto a que la aceleración no se puede mantener constante. A medida que se va más rápido, el coche debe cambiar a marchas más largas, en las que la aceleración es menor. En una situación real lo que ocurriría (habitualmente) es que el infractor reduciría y sería alcanzado más fácilmente, o que la Guardia Civil, marchando más lentamente, lo alcanzaría más tarde. | Este problema no es realista en cuanto a que la aceleración no se puede mantener constante. A medida que se va más rápido, el coche debe cambiar a marchas más largas, en las que la aceleración es menor. En una situación real lo que ocurriría (habitualmente) es que el infractor reduciría y sería alcanzado más fácilmente, o que la Guardia Civil, marchando más lentamente, lo alcanzaría más tarde. | ||
[[Categoría:Problemas de cinemática de la partícula (GIOI)]] | [[Categoría:Problemas de cinemática de la partícula (GIOI)]] | ||
[[Categoría:Problemas de cinemática del movimiento rectilíneo (GIOI)]] | [[Categoría:Problemas de cinemática del movimiento rectilíneo (GIOI)]] | ||
Revisión de 12:38 24 sep 2019
1 Enunciado
Las especificaciones del Seat Exeo establecen que va de 0 a 100 km/h en 9.2 s. ¿Cuánto vale su aceleración media en este periodo? ¿Cuánto vale el tiempo mínimo para atravesar un cruce de 15 m de anchura, si parte de estar parado en un semáforo? ¿Con qué velocidad llegaría al otro lado?
Un Seat León FR amarillo circula por la carretera a 160 km/h y pasa junto a un coche de la Guardia Civil parado en el arcén. Sabiendo que la benemérita usa un Seat Exeo, ¿cuál es el mínimo tiempo que tarda en alcanzar al Seat León si este no reduce su velocidad? ¿A qué distancia del punto donde estába parado lo alcanza? ¿Qué velocidad tiene el coche patrulla cuando alcanza al infractor?
2 Aceleración media
La aceleración media la hallamos a partir del cociente entre el incremento de la velocidad y el tiempo empleado en este incremento
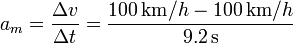
Aquí el único problema es la mezcla de unidades, que resolvemos introduciendo los factores de conversión
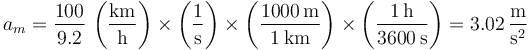
Esto equivale a una aceleración de 0.31g, que no es muy intensa.
Para atravesar un cruce de 15\,m en máxima aceleración partiendo del reposo serequiere un tiempo
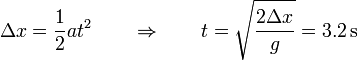
y la velocidad al llegar al otro lado del cruce es
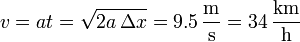
3 Alcance
La forma más rápida que tiene el coche patrulla de alcanzar al infractor es marchando a máxima aceleración. Si levantan el pie del acelerador, la velocidad se incrementará más lentamente y por tanto tardará más en alcanzarlo.
Si admitimos que el Exeo es capaz de mantener la aceleración que hemos calculado antes durante un tiempo largo, el alcance se produce cuando la distancia recorrida por el Exeo es la misma que la recorrida por el León, esto es
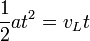
siendo
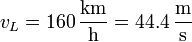
esto nos da el tiempo de alcance
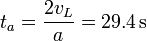
La distancia recorrida hasta el alcance vale
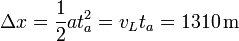
Ahora bien, ¿cuál es la velocidad instantánea del Exeo en este momento? La media es la misma, pues ha recorrido la misma distancia en el mismo tiempo, pero puesto que partía del reposo, la instantánea debe ser mayor. Concretamente
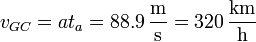
lo cual es absurdo, pues se trata de un Seat Exeo, no de un Fórmula 1.
Este problema no es realista en cuanto a que la aceleración no se puede mantener constante. A medida que se va más rápido, el coche debe cambiar a marchas más largas, en las que la aceleración es menor. En una situación real lo que ocurriría (habitualmente) es que el infractor reduciría y sería alcanzado más fácilmente, o que la Guardia Civil, marchando más lentamente, lo alcanzaría más tarde.





