Entrar Página Discusión Historial Go to the site toolbox

Movimiento oscilatorio

De Laplace

(Diferencias entre revisiones)
(→Caso subamortiguado)
(→Caso subamortiguado)
Línea 112: Línea 112:
</center>
</center>
Así pues, la solución es el producto de dos factores. Uno de ellos incluye cosenos y senos, por lo que es oscilante. El otro es una exponencial con exponente negativo, por lo que es decreciente. El resultado es una función que oscila con frecuencia angular <math>\omega=\sqrt{\omega_0^2-\gamma^2}</math> y con amplitud decreciente.
Así pues, la solución es el producto de dos factores. Uno de ellos incluye cosenos y senos, por lo que es oscilante. El otro es una exponencial con exponente negativo, por lo que es decreciente. El resultado es una función que oscila con frecuencia angular <math>\omega=\sqrt{\omega_0^2-\gamma^2}</math> y con amplitud decreciente.
 +
[[Imagen:oscilacion_amortiguada.png|right]]
 +
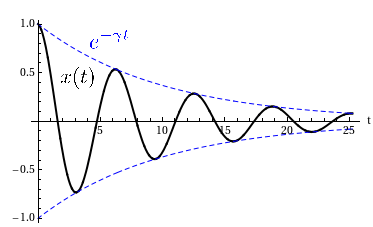
La línea negra en la figura adjunta muestra la evolución en el tiempo de la posición de la masa. La línea azul de trazas indica la evolución de la amplitud de la oscilación. Es intereante señalar que en este caso tenemos dos escalas de tiempo relevantes en el problema. Por una lado, el período de las oscilaciones es
 +
<center><math>T=\frac{2\pi}{\omega}>T_0=\frac{2\pi}{\omega_0}</math></center>
 +
<math>T_0</math> es el periódo correspondiente a la frecuencia propia <math>\omega_0</math>. Como <math>\omega<\omega_0</math>, el período de oscialción es algo mayor que <math>T_0</math>.
 +
 +
Por otro lado tenemos el tiempo típico de decreciiento de la amplitud. En una función exponencial, se define como el tiempo necesario para que el valor se <math>1/e</math> veces el original. Es decir, en este caso tenemos
 +
<center><math>\tau_{\gamma}=1/\gamma</math></center>
 +
Físicamente, esto significa que despues de un tiempo <math>t\simeq5\tau_{\gamma}</math> el valor de la amplitud es prácticamente cero.
 +
 +
En esta situación de oscilación subamortiguada el rozamiento es pequeño, por lo que tenemos que
 +
<center>
 +
<math>
 +
\tau_{\gamma}>T
 +
</math>
 +
</center>
 +
Es decir, hacen falta varias oscilaciones para que el rozamiento detenga la oscilación de la masa. Esto es claramente visible en la figura.
 +
 +
=====Caso sobreamortiguado =====
 +
Consideremos ahora la situación en la que el rozamiento es muy grande
 +
<center><math>\omega_0^2<\gamma^2</math></center>
 +
Ahora, el radicando es positivo, por lo que las dos soluciones de la ecuación característica son reales. Si definimos
 +
<center>
 +
<math>
 +
p= \sqrt{\gamma^2-\omega_0^2}
 +
</math>
 +
</center>
 +
los valores de <math>\lambda</math> son
 +
<center>
 +
<math>
 +
\lambda_{\pm}(t)=-\gamma\pm \sqrt{\gamma^2-\omega_0^2}=
 +
-\gamma\pm p
 +
</math>
 +
</center>
 +
Observermos que, de su definición, <math>p<\gamma</math> , por lo que los dos valores <math>\lambda_{\pm}</math> son negativos. Como la solución general es
 +
<center>
 +
<math>
 +
x(t)=A_+e^{(-\gamma+p)t}+A_-e^{(-\gamma-p)t}=
 +
A_+e^{-(\gamma-p)t}+A_-e^{-(\gamma+p)t}
 +
</math>
 +
</center>
 +
Las dos exponenciales tienen exponentes negativos. Por tanto, las oscilaciones decaen en el tiempo. El tiempo típico de decaimiento está controlado por el exponente de valor absoluto más pequeño, pues de las dos funciones es la que tarda más en disminuir su valor. Por tanto
 +
<center>
 +
<math>
 +
\tau=\frac{1}{\gamma-p}
 +
</math>
 +
</center>
 +
=====Amortiguamento crítico =====
 +
Ahora tenemos la condición
 +
<center>
 +
<math>
 +
\omega_0^2=\gamma^2
 +
</math>
 +
</center>
 +
Cuando ocurre esto, el radicando de la ecuación característica es cero, por lo que existe una única solución de la forma <math>e^{\lambda t}</math>. Pero la ecuación diferencial es de segundo orden, por lo que la solución general debe ser una combinación lineal de dos funciones distintas. En este caso, se debe buscar otra solución de la forma <math>te^{-\gamma t}</math>, que se puede comprobar que es solución de la ecuación diferencial cuando <math>\omega_0^2=\gamma^2</math>. Entonces, la solución general es
 +
<center>
 +
<math>
 +
x(t) = e^{-\gamma t}\left(A_1+A_2t\right)
 +
</math>
 +
</center>
 +
De nuevo es una función decreciente en el tiempo, es decir, la amplitud de las oscilaciones tiende a cero
==Problemas==
==Problemas==

Revisión de 13:40 11 mar 2009

Contenido

1 Movimiento oscilatorio

2 Movimiento armónico simple

3 Representación matemática del MAS: fase, periodo y frecuencia

4 Energía del MAS

5 Sistemas oscilantes: péndulo simple y péndulo físico

6 Oscilaciones amortiguadas y forzadas

6.1 Oscilaciones amortiguadas

Consideremos el caso de una masa m unida a un muelle de consntante recuperadora k y longitud natural nula,y sometida además a una fuerza de rozamiento proporcional a la velocidad. En este caso, las fuerzas que actúan sobre la masa son la fuerza recuperadora del muelle y la fuerza de rozamiento

\begin{array}{lcr} \mathbf{F}_k=-k\mathbf{r}&& \mathbf{F}_v=-b\mathbf{v} \end{array}

El coeficiente b indica la intensidad de la fuerza del rozamiento. El signo negativo indica que esta fuerza se opone siempre a la velocidad.

Si suponemos que el movimiento se produce en una dimensión, escogiendo el eje X a lo largo de la dirección del movimiento podemos expresar las fuerzas como

\begin{array}{lcr} F_k=-kx&& F_v=-b\dot{x} \end{array}

El movimiento de la masa viene determinado por la Segunda Ley de Newton

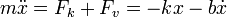
m\ddot{x}=F_k+F_v=-kx-b\dot{x}

Reordenamos los términos de la ecuación y la escribimos

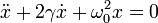
\ddot{x}+2\gamma\dot{x}+\omega_0^2x=0

siendo

\begin{array}{lccr} \gamma=b/2&&&\omega_0^2=k/m \end{array}

El parámetro γ indica la intensidad del rozamiento y ω0 es la frecuencia que tendría el oscilador si no hubiera rozamiento. Recibe el nombre de frecuencia natural.

6.1.1 Soluciones de la ecuación diferencial

La ecuación que determina el movimiento de la masa es la del oscilador armónico con un término añadido proporcional a la velocidad, que representa el rozamiento al que está sometida la masa. Es una ecuación diferencial de coeficientes constantes. La técnica para resolver este tipo de ecuaciones es buscar soluciones de la forma

x(t) = Aeλt

La idea es que al derivar esta función el resultado es ella misma multiplicada por el parámetro λ. Tenemos

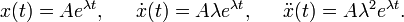
\begin{array}{ccccc} x(t)=Ae^{\lambda t},& &\dot{x}(t)=A\lambda e^{\lambda t}, & & \ddot{x}(t)=A\lambda^2 e^{\lambda t}. \end{array}

Sustituyendo en la ecuación, podemos eliminar el factor común Aeλt, pues es siempre distinto de cero. Con ello obtenemos la ecuación que debe cumplir λ para que x(t) sea solución

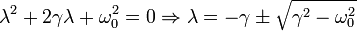
\lambda^2 + 2\gamma \lambda + \omega_0^2=0 \Rightarrow \lambda=-\gamma\pm\sqrt{\gamma^2-\omega_0^2}

Obtenemos dos posibles valores de λ. La solución general es una combinación lineal de las dos funciones definidas por estos dos posibles valores

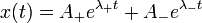
x(t) = A_+e^{\lambda_+t}+A_-e^{\lambda_-t}

Aquí, λ + corersponde a la solución con la raíz positiva y λ − a la solución con la raíz negativa.

El comportamiento de la solución depende de como es el radicando de la ecuación de segundo grado. Examinemos cada uno de los casos.

6.1.1.1 Caso subamortiguado

Veamos primero la situación en la que el rozamiento es pequeño. Entonces se cumple

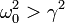
\omega_0^2>\gamma^2

Cuando se cumple esta condición el radicando es negativo, con lo cual la raíz cuadrada es un número imaginario puro. Si definimos 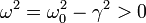\omega^2=\omega_0^2-\gamma^2>0, los valores de λ quedan

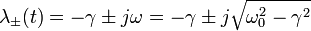
\lambda_{\pm}(t)=-\gamma\pm j \omega=-\gamma\pm j\sqrt{\omega_0^2-\gamma^2}

siendo 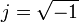j=\sqrt{-1}la unidad imaginaria. La solución general de la ecuación es de la forma

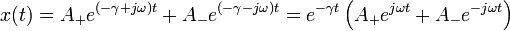
x(t)=A_+e^{(-\gamma+j\omega)t}+A_-e^{(-\gamma-j\omega)t}= e^{-\gamma t}\left(A_+e^{j\omega t}+A_-e^{-j\omega t}\right)

Los coeficientes A + , A − deben ser tales que x(t) sea real. Recordando que según la fórmula de Euler

ejα = cos(α) + jsen(α)

vemos que la solución general se puede escribir como

x(t)= e^{-\gamma t}\left[a_1\cos(\omega t)+a_2\mathrm{sen}(\omega t)\right]

Así pues, la solución es el producto de dos factores. Uno de ellos incluye cosenos y senos, por lo que es oscilante. El otro es una exponencial con exponente negativo, por lo que es decreciente. El resultado es una función que oscila con frecuencia angular 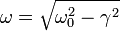\omega=\sqrt{\omega_0^2-\gamma^2} y con amplitud decreciente.

La línea negra en la figura adjunta muestra la evolución en el tiempo de la posición de la masa. La línea azul de trazas indica la evolución de la amplitud de la oscilación. Es intereante señalar que en este caso tenemos dos escalas de tiempo relevantes en el problema. Por una lado, el período de las oscilaciones es

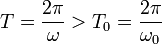
T=\frac{2\pi}{\omega}>T_0=\frac{2\pi}{\omega_0}

T0 es el periódo correspondiente a la frecuencia propia ω0. Como ω < ω0, el período de oscialción es algo mayor que T0.

Por otro lado tenemos el tiempo típico de decreciiento de la amplitud. En una función exponencial, se define como el tiempo necesario para que el valor se 1 / e veces el original. Es decir, en este caso tenemos

τγ = 1 / γ

Físicamente, esto significa que despues de un tiempo 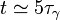t\simeq5\tau_{\gamma} el valor de la amplitud es prácticamente cero.

En esta situación de oscilación subamortiguada el rozamiento es pequeño, por lo que tenemos que

τγ > T

Es decir, hacen falta varias oscilaciones para que el rozamiento detenga la oscilación de la masa. Esto es claramente visible en la figura.

6.1.1.2 Caso sobreamortiguado

Consideremos ahora la situación en la que el rozamiento es muy grande

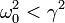
\omega_0^2<\gamma^2

Ahora, el radicando es positivo, por lo que las dos soluciones de la ecuación característica son reales. Si definimos

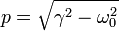
p= \sqrt{\gamma^2-\omega_0^2}

los valores de λ son

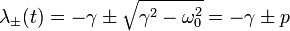
\lambda_{\pm}(t)=-\gamma\pm \sqrt{\gamma^2-\omega_0^2}= -\gamma\pm p

Observermos que, de su definición, p < γ , por lo que los dos valores 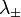\lambda_{\pm} son negativos. Como la solución general es

x(t) = A + e( − γ + p)t + A − e( − γ − p)t = A + e − (γ − p)t + A − e − (γ + p)t

Las dos exponenciales tienen exponentes negativos. Por tanto, las oscilaciones decaen en el tiempo. El tiempo típico de decaimiento está controlado por el exponente de valor absoluto más pequeño, pues de las dos funciones es la que tarda más en disminuir su valor. Por tanto

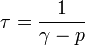
\tau=\frac{1}{\gamma-p}

6.1.1.3 Amortiguamento crítico

Ahora tenemos la condición

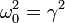
\omega_0^2=\gamma^2

Cuando ocurre esto, el radicando de la ecuación característica es cero, por lo que existe una única solución de la forma eλt. Pero la ecuación diferencial es de segundo orden, por lo que la solución general debe ser una combinación lineal de dos funciones distintas. En este caso, se debe buscar otra solución de la forma te − γt, que se puede comprobar que es solución de la ecuación diferencial cuando 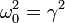\omega_0^2=\gamma^2. Entonces, la solución general es

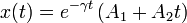
x(t) = e^{-\gamma t}\left(A_1+A_2t\right)

De nuevo es una función decreciente en el tiempo, es decir, la amplitud de las oscilaciones tiende a cero

7 Problemas

Artículo completo: Problemas de movimiento oscilatorio
Obtenido de "http://tesla.us.es/wiki/index.php/Movimiento_oscilatorio"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace