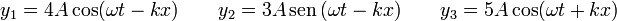Superposición de dos y tres señales
De Laplace
(Diferencias entre revisiones)
(→Primer caso) |
(→Primer caso) |
||
| Línea 13: | Línea 13: | ||
Debemos sumar las señales | Debemos sumar las señales | ||
| - | <center><math>y_1= A \cos(\omega t - kx) | + | <center><math>y_1= A \cos(\omega t - kx)</math>{{qquad}}{{qquad}}<math>y_2 = A\,\mathrm{sen}\,(\omega t-kx)</math></center> |
===Segundo caso=== | ===Segundo caso=== | ||
Revisión de 20:34 10 mar 2009
Contenido |
1 Enunciado
Considere los casos de superposición siguientes
Para cada uno de los casos, determine la ecuación de la señal resultante, ¿es una onda viajera o una estacionaria?
2 Solución
2.1 Primer caso
Debemos sumar las señales
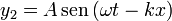
2.2 Segundo caso

2.3 Tercer caso
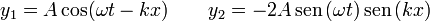
2.4 Cuarto caso