Entrar Página Discusión Historial Go to the site toolbox

Campo magnético producido por dos hilos paralelos

De Laplace

(Diferencias entre revisiones)
(→En el eje OX (y=0))
m (→Campo de dos hilos)
 
(2 ediciones intermedias no se muestran.)
Línea 47: Línea 47:
===Campo de dos hilos===
===Campo de dos hilos===
-
Cuando tenemos dos hilos paralelos aplicamos el principio de superposición. Si uno está sobre <math>x_1=a</math> y el otro sobre <math>x_2=-a</math> la expresión del campo total será la suma de dos expresiones como la anterior, una con <math>x-a</math> y la otra xon <math>x-(-a)=x+a</math>
+
Cuando tenemos dos hilos paralelos aplicamos el principio de superposición. Si uno está sobre <math>x_1=a</math> y el otro sobre <math>x_2=-a</math> la expresión del campo total será la suma de dos expresiones como la anterior, una con <math>x-a</math> y la otra con <math>x-(-a)=x+a</math>
<center><math>\vec{B}=\frac{\mu_0}{2\pi}\left(\frac{I_1}{x-a}+\frac{I_2}{x+a}\right)\vec{\jmath}</math></center>
<center><math>\vec{B}=\frac{\mu_0}{2\pi}\left(\frac{I_1}{x-a}+\frac{I_2}{x+a}\right)\vec{\jmath}</math></center>
Línea 55: Línea 55:
<center><math>I_1=I_2=I\qquad\Rightarrow\qquad \vec{B}=\frac{\mu_0I}{2\pi}\left(\frac{1}{x-a}+\frac{1}{x+a}\right)\vec{\jmath}=\frac{\mu_0Ix}{\pi(x^2-a^2)}\vec{\jmath}</math></center>
<center><math>I_1=I_2=I\qquad\Rightarrow\qquad \vec{B}=\frac{\mu_0I}{2\pi}\left(\frac{1}{x-a}+\frac{1}{x+a}\right)\vec{\jmath}=\frac{\mu_0Ix}{\pi(x^2-a^2)}\vec{\jmath}</math></center>
 +
<center>[[Archivo:suma-corrientes-paralelas.png]]</center>
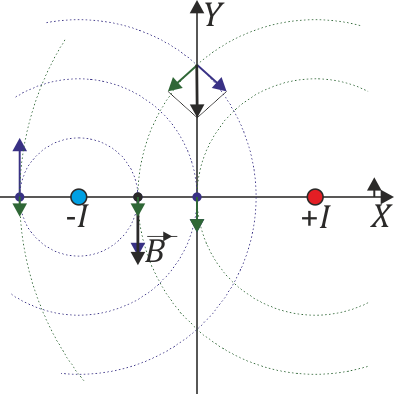
:Este campo tiene la particularidad de que en <math>x=0</math> se anula. En ese punto la regla de la mano derecha implica que el campo de un hilo vaya en sentido opuesto al del otro y se cancelen.
:Este campo tiene la particularidad de que en <math>x=0</math> se anula. En ese punto la regla de la mano derecha implica que el campo de un hilo vaya en sentido opuesto al del otro y se cancelen.
Línea 62: Línea 63:
<center><math>I_1=I\qquad I_2=-I\qquad\Rightarrow\qquad \vec{B}=\frac{\mu_0I}{2\pi}\left(\frac{1}{x-a}-\frac{1}{x+a}\right)\vec{\jmath}=\frac{\mu_0Ia}{\pi(x^2-a^2)}\vec{\jmath}</math></center>
<center><math>I_1=I\qquad I_2=-I\qquad\Rightarrow\qquad \vec{B}=\frac{\mu_0I}{2\pi}\left(\frac{1}{x-a}-\frac{1}{x+a}\right)\vec{\jmath}=\frac{\mu_0Ia}{\pi(x^2-a^2)}\vec{\jmath}</math></center>
 +
<center>[[Archivo:suma-corrientes-antiparalelas.png]]</center>
:En x=0 este campo no es nulo, ya que se suman los dos campos individuales, que van en el mismo sentido.
:En x=0 este campo no es nulo, ya que se suman los dos campos individuales, que van en el mismo sentido.
Línea 111: Línea 113:
;Corrientes antiparalelas: En ese caso  
;Corrientes antiparalelas: En ese caso  
-
<center><math>I_1=I\qquad I_2=-I\qquad\Rightarrow\qquad \vec{B}=-\frac{\mu_0a\vec{\jmath}}{2\pi(a^2+y^2)}</math></center>
+
<center><math>I_1=I\qquad I_2=-I\qquad\Rightarrow\qquad \vec{B}=-\frac{\mu_0Ia\vec{\jmath}}{\pi(a^2+y^2)}</math></center>
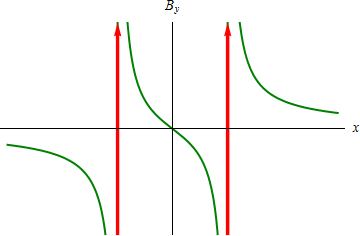
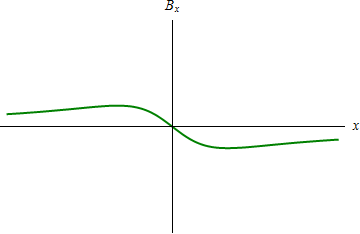
Gráficamente, el primer caso tiene un máximo y un mínimo, con paso por 0 en el origen, y en el segundo tiene forma de campana.
Gráficamente, el primer caso tiene un máximo y un mínimo, con paso por 0 en el origen, y en el segundo tiene forma de campana.

última version al 13:08 25 mar 2019

Contenido

1 Enunciado

Dos hilos paralelos se hallan situados paralelamente al eje Z, situados sobre 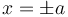x = \pm a, y = 0. Determine el valor del campo magnético en todos los puntos del plano x = 0, y en todos los puntos del plano y = 0 en los dos casos siguientes:

  1. Por los hilos circulan corrientes paralelas + I0.
  2. Por los hilos circulan corrientes antiparalelas \pm I_0.

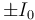Para el caso particular 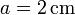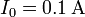a=2\,\mathrm{cm} I_0=0.1\,\mathrm{A}, ¿cuánto vale el campo magnético en el origen de coordenadas para los dos casos anteriores?

2 En el eje OX (y=0)

2.1 Campo de un solo hilo

El campo magnético creado por un hilo rectilíneo situado en el eje OZ y por el cual circula una corriente I tiene la expresión

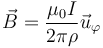
\vec{B}=\frac{\mu_0I}{2\pi\rho}\vec{u}_\varphi

donde ρ es la distancia al eje OZ. En función de las coordenadas cartesianas

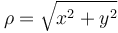
\rho = \sqrt{x^2+y^2}

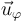\vec{u}_\varphi es el vector unitario tangente a circunferencias alrededor de OZ que lo tienen como eje. Este vector depende de la posición, según la fórmula general vista al estudiar las coordenadas polares y cilíndricas

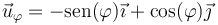
\vec{u}_\varphi=-\mathrm{sen}(\varphi)\vec{\imath}+\cos(\varphi)\vec{\jmath}
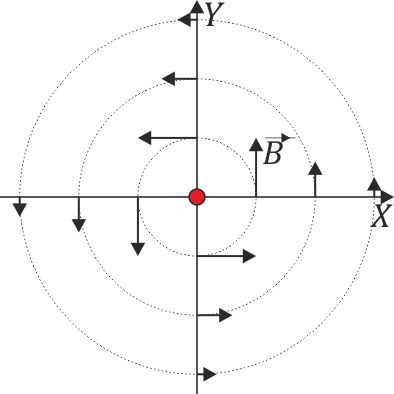
Archivo:Campo-hilo-infinito.png

Para particularizar este campo en los puntos del eje X, debemos distinguir si estamos en x > 0 o en x < 0.

x > 0
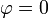En este caso la distancia al eje es la propia coordenada x mientras que vector para los puntos de OX no es itro que el unitario \vec{\jmath} (lo cual se puede comprobar haciendo \varphi=0 en la expresión anterior). Por tanto, el campo en este semieje se puede escribir
\vec{B}=\frac{\mu_0I}{2\pi x}\vec{\jmath}\qquad\qquad (y=0,x>0)
x < 0
En el semieje negativo (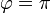\varphi=\pi) la distancia es |x| y el unitario es 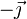-\vec{\jmath} por lo que el campo vale
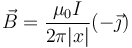
\vec{B}=\frac{\mu_0I}{2\pi|x|}(-\vec{\jmath})
pero para valores negativos de x
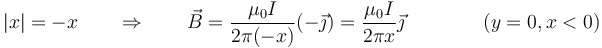
|x| = -x\qquad \Rightarrow\qquad \vec{B}=\frac{\mu_0I}{2\pi(-x)}(-\vec{\jmath})=\frac{\mu_0I}{2\pi x}\vec{\jmath}\qquad\qquad (y=0,x < 0)

Es decir, para todo el eje OX la expresión del campo magnético es

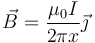
\vec{B}=\frac{\mu_0I}{2\pi x}\vec{\jmath}

Si el hilo de corriente no se encuentra en x0 = 0 sino sobre otro punto x0 = a tenemos que hacer una traslación cambiando x por x − a y queda

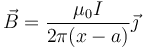
\vec{B}=\frac{\mu_0I}{2\pi (x-a)}\vec{\jmath}

2.2 Campo de dos hilos

Cuando tenemos dos hilos paralelos aplicamos el principio de superposición. Si uno está sobre x1 = a y el otro sobre x2 = − a la expresión del campo total será la suma de dos expresiones como la anterior, una con x − a y la otra con x − ( − a) = x + a

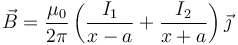
\vec{B}=\frac{\mu_0}{2\pi}\left(\frac{I_1}{x-a}+\frac{I_2}{x+a}\right)\vec{\jmath}
Corrientes paralelas
En el caso particular de corrientes paralelas
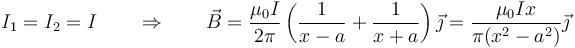
I_1=I_2=I\qquad\Rightarrow\qquad \vec{B}=\frac{\mu_0I}{2\pi}\left(\frac{1}{x-a}+\frac{1}{x+a}\right)\vec{\jmath}=\frac{\mu_0Ix}{\pi(x^2-a^2)}\vec{\jmath}
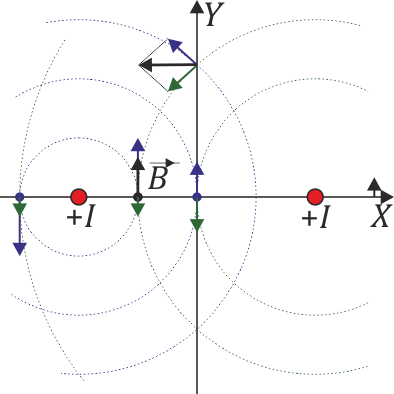
Archivo:suma-corrientes-paralelas.png
Este campo tiene la particularidad de que en x = 0 se anula. En ese punto la regla de la mano derecha implica que el campo de un hilo vaya en sentido opuesto al del otro y se cancelen.
Archivo:Campo-hilos-paralelos-x.png
Corrientes antiparalelas
Si las corrientes van en sentidos opuestos
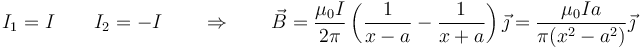
I_1=I\qquad I_2=-I\qquad\Rightarrow\qquad \vec{B}=\frac{\mu_0I}{2\pi}\left(\frac{1}{x-a}-\frac{1}{x+a}\right)\vec{\jmath}=\frac{\mu_0Ia}{\pi(x^2-a^2)}\vec{\jmath}
Archivo:suma-corrientes-antiparalelas.png
En x=0 este campo no es nulo, ya que se suman los dos campos individuales, que van en el mismo sentido.
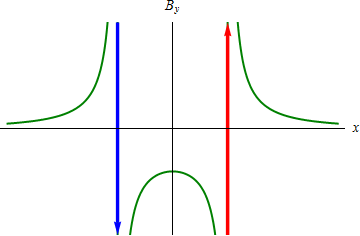
Archivo:Campo-hilos-antiparalelos-x.png
En esta gráfica un valor positivo quiere decir que va en el sentido de 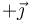+\vec{\jmath} y uno negativo que va en el de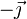 -\vec{\jmath}

3 En el eje OY (x=0)

3.1 Campo de un hilo

En el caso del eje OY necesitamos la expresión en cartesianas del campo de un hilo para cualquier punto del espacio. La razón de que haya que usar cartesianas es que posteriormente debemos aplicar superposición y ésta solo se hace de forma sencilla si empleamos la base en cartesianas.

Sustituyendo la expresión de 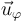\vec{u}_\varphi en el campo magnético de un hilo situado en OZ

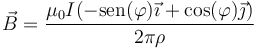
\vec{B}=\frac{\mu_0I(-\mathrm{sen}(\varphi)\vec{\imath}+\cos(\varphi)\vec{\jmath})}{2\pi\rho}

Para pasar a las coordenadas cartesianas multiplicamos arriba y abajo por ρ

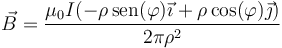
\vec{B}=\frac{\mu_0I(-\rho\,\mathrm{sen}(\varphi)\vec{\imath}+\rho\cos(\varphi)\vec{\jmath})}{2\pi\rho^2}

pero

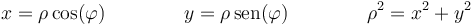
x=\rho\cos(\varphi)\qquad\qquad y=\rho\,\mathrm{sen}(\varphi)\qquad\qquad \rho^2=x^2+y^2

por lo que el campo se puede poner como

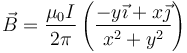
\vec{B}=\frac{\mu_0I}{2\pi}\left(\frac{-y\vec{\imath}+x\vec{\jmath}}{x^2+y^2}\right)

Si el hilo no está sobre el eje OZ, sino sobre x0 = a hacemos la misma traslación que antes (lo cual solo es posible una vez que se ha pasado a cartesianas y aparecen x e y)

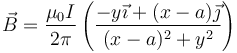
\vec{B}=\frac{\mu_0I}{2\pi}\left(\frac{-y\vec{\imath}+(x-a)\vec{\jmath}}{(x-a)^2+y^2}\right)

3.2 Campo de dos hilos

Como antes, la expresión general la obtenemos sumando los campos de los dos hilos

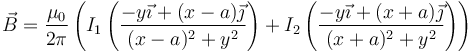
\vec{B}=\frac{\mu_0}{2\pi}\left(I_1\left(\frac{-y\vec{\imath}+(x-a)\vec{\jmath}}{(x-a)^2+y^2}\right)+I_2\left(\frac{-y\vec{\imath}+(x+a)\vec{\jmath}}{(x+a)^2+y^2}\right)\right)

que, sobre el eje Y (x=0) se reduce a

\vec{B}=\frac{\mu_0}{2\pi}\left(I_1\left(\frac{-y\vec{\imath}-a\vec{\jmath}}{a^2+y^2}\right)+I_2\left(\frac{-y\vec{\imath}+a\vec{\jmath}}{a^2+y^2}\right)\right)=\frac{\mu_0(-y(I_1+I_2)\vec{\imath}+a(I_2-I_1)\vec{\jmath}}{2\pi(a^2+y^2)}
Corrientes paralelas
Si las dos corrientes van el mismo sentido, el campo se queda en
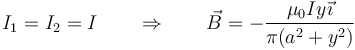
I_1=I_2=I\qquad\Rightarrow\qquad \vec{B}=-\frac{\mu_0Iy\vec{\imath}}{\pi(a^2+y^2)}
Esta expresión se anula en y=0, tal como vimos antes.
Archivo:Campo-hilos-paralelos-y.png
Corrientes antiparalelas
En ese caso
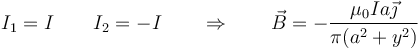
I_1=I\qquad I_2=-I\qquad\Rightarrow\qquad \vec{B}=-\frac{\mu_0Ia\vec{\jmath}}{\pi(a^2+y^2)}

Gráficamente, el primer caso tiene un máximo y un mínimo, con paso por 0 en el origen, y en el segundo tiene forma de campana.

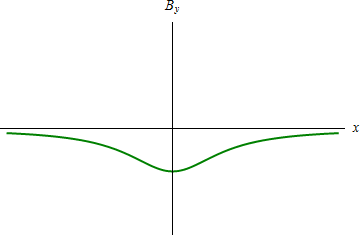
Archivo:Campo-hilos-antiparalelos-y.png

Nótese que también la dirección de los campos cambia. En un caso es puramente en la dirección del eje X y en el otro en la de Y.

Obtenido de "http://tesla.us.es/wiki/index.php/Campo_magn%C3%A9tico_producido_por_dos_hilos_paralelos"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 13:08, 25 mar 2019. - Esta página ha sido visitada 13.532 veces. - Aviso legal - Acerca de Laplace